121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
方法一:贪心
class Solution {public int maxProfit(int[] prices) {// 找到一个最小的购入点int low = Integer.MAX_VALUE;// res不断更新,直到数组循环完毕int res = 0;for(int i = 0; i < prices.length; i++){low = Math.min(prices[i], low);res = Math.max(prices[i] - low, res);}return res;}
}
这段代码是解决“买卖股票的最佳时机”问题(LeetCode上的第121题)的Java实现。这个问题要求你给定一个整数数组prices,其中prices[i]是第i天一支股票的价格。你想要设计一个算法来找到最大的可能利润。你可以尽可能地完成更多的交易(多次买卖一支股票),但是你必须卖出股票之后才能再次买入。
在这段代码中:
- 定义了一个变量
low来跟踪目前为止遇到的最低价格,初始值设为Integer.MAX_VALUE,确保任何实际的价格都会小于这个初始值。 - 定义了一个变量
res来跟踪目前为止能获得的最大利润,初始值设为0。 - 使用for循环遍历整个价格数组
prices:- 在每次循环中,更新
low的值,使其成为当前价格prices[i]和当前low值之间的较小者。这样做是为了确保low始终是最新的最低价格。 - 同时,更新
res的值,使其成为当前价格减去最低价格prices[i] - low和当前res值之间的较大者。这样做是为了确保res始终是迄今为止可能的最大利润。
- 在每次循环中,更新
- 循环结束后,
res变量的值就是最大可能利润,直接返回。
这种方法的时间复杂度为O(n),其中n是价格数组prices的长度,因为每个元素只被访问一次。空间复杂度为O(1),因为只使用了固定的几个额外变量,与输入数组的大小无关。这种解法是线性扫描算法的一个典型应用,非常高效且易于理解和实现。
方法二:动态规划-版本一
// 解法1
class Solution {public int maxProfit(int[] prices) {if (prices == null || prices.length == 0) return 0;int length = prices.length;// dp[i][0]代表第i天持有股票的最大收益// dp[i][1]代表第i天不持有股票的最大收益int[][] dp = new int[length][2];int result = 0;dp[0][0] = -prices[0];dp[0][1] = 0;for (int i = 1; i < length; i++) {dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);}return dp[length - 1][1];}
}
这段代码是另一种解决“买卖股票的最佳时机”问题的方法,但这次使用的是动态规划(Dynamic Programming)。这个解法考虑了在每一天结束时持有或不持有股票两种状态下的最大收益。
在代码中定义了二维数组dp,其中:
dp[i][0]表示在第i天结束时持有股票可以获得的最大收益。dp[i][1]表示在第i天结束时不持有股票可以获得的最大收益。
初始化dp[0][0]为-prices[0],表示在第一天购买股票的成本;dp[0][1]为0,表示在第一天不持有股票的收益。
接下来,通过遍历数组并更新dp中的值,根据前一时刻的状态计算出当前时刻的状态:
- 对于
dp[i][0],它要么保持前一天持有股票的状态dp[i - 1][0],要么在当天买入股票,即-prices[i]。选择两者中的较大值作为当天持有股票的最大收益。 - 对于
dp[i][1],它要么保持前一天不持有股票的状态dp[i - 1][1],要么在当天卖出股票,即dp[i - 1][0] + prices[i]。选择两者中的较大值作为当天不持有股票的最大收益。
最终,dp[length - 1][1]给出的就是最后一天不持有股票时的最大收益,也就是我们所求的最大利润。
让我们来演示一下这个方法的工作原理,假设我们有如下的股票价格数组:
prices = [7, 1, 5, 3, 6, 4]
我们可以计算出对应的dp数组。
def max_profit(prices):if not prices:return 0length = len(prices)dp = [[0] * 2 for _ in range(length)]dp[0][0] = -prices[0]dp[0][1] = 0for i in range(1, length):dp[i][0] = max(dp[i - 1][0], -prices[i])dp[i][1] = max(dp[i - 1][0] + prices[i], dp[i - 1][1])return dp[length - 1][1]# 示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
# 计算最大利润
max_profit_value = max_profit(prices)
# 计算dp数组以便展示
dp_array = [[-prices[0], 0]] + [[0, 0] for _ in range(len(prices) - 1)]
for i in range(1, len(prices)):dp_array[i][0] = max(dp_array[i - 1][0], -prices[i])dp_array[i][1] = max(dp_array[i - 1][0] + prices[i], dp_array[i - 1][1])
max_profit_value, dp_array
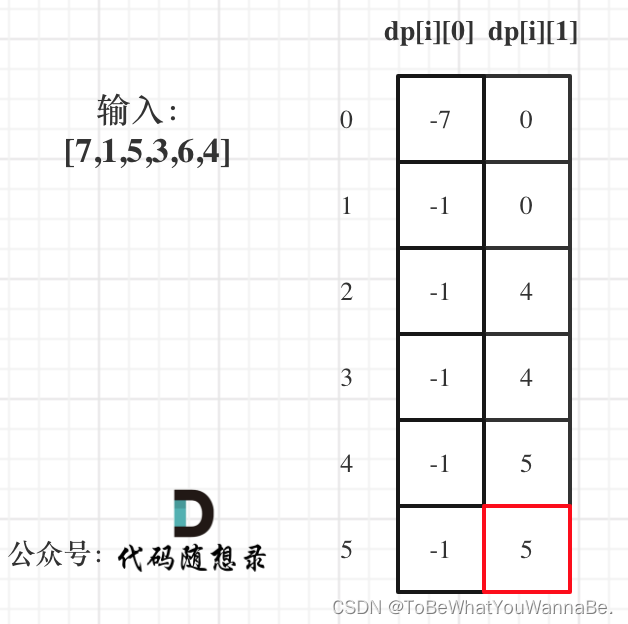
(5, [[-7, 0], [-1, 0], [-1, 4], [-1, 4], [-1, 5], [-1, 5]])
根据动态规划方法计算得到,给定股票价格数组 [7, 1, 5, 3, 6, 4] 的情况下,最大利润为 5。
同时,计算过程中得到的 dp 数组如下:
dp[0]为[-7, 0],表示第一天持有股票的收益为-7(买入成本),不持有股票的收益为0。dp[1]为[-1, 0],表示第二天持有股票的收益更新为-1(新的买入机会),不持有股票的收益仍为0。dp[2]为[-1, 4],表示第三天持有股票的收益保持-1,不持有股票的收益更新为4(卖出去的收益)。dp[3]为[-1, 4],表示第四天持有股票的收益保持-1,不持有股票的收益保持4(没有更好的卖出机会)。dp[4]为[-1, 5],表示第五天持有股票的收益保持-1,不持有股票的收益更新为5(新的卖出机会)。dp[5]为[-1, 5],表示第六天持有股票的收益保持-1,不持有股票的收益保持5(没有更好的卖出机会)。
最终,dp 数组的最后一个元素 [ -1, 5 ] 中的 5 就是我们求得的最大利润。
方法三:动态规划(二维数组)
class Solution {public int maxProfit(int[] prices) {int len = prices.length;int dp[][] = new int[2][2];dp[0][0] = - prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++){dp[i % 2][0] = Math.max(dp[(i - 1) % 2][0], - prices[i]);dp[i % 2][1] = Math.max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);}return dp[(len - 1) % 2][1];}
}
这段代码展示了另一种优化过的动态规划方法,用于解决同样的“买卖股票的最佳时机”问题。与之前的版本相比,这个版本的空间复杂度从 O(n) 减少到了 O(1),因为它只使用了一个固定大小的二维数组 dp 来存储当前和前一个状态,而不是完整的 n×2 矩阵。
在代码中,dp 数组的维度被设定为 2×2,其中第一个索引用于区分当前和前一个状态,第二个索引仍然用于表示持有 (dp[i][0]) 或不持有 (dp[i][1]) 股票的情况。通过取模运算 (i % 2),可以在这两个状态之间交替,从而节省空间。
代码的关键点如下:
- 初始化
dp[0][0]为-prices[0],表示在第一天购买股票的成本。 - 初始化
dp[0][1]为0,表示在第一天不持有股票的收益。 - 在循环中,更新
dp[i % 2][0]和dp[i % 2][1]的值,其中i是当前处理的天数索引。
这种实现方式有效地利用了空间,因为无论输入数组的长度如何,使用的空间总是固定的。现在,让我们基于相同的示例 [7, 1, 5, 3, 6, 4] 来演示这个优化后的算法是如何工作的。我们将手动模拟这个过程,并计算出最大利润。
def max_profit_optimized(prices):if not prices:return 0dp = [[0] * 2 for _ in range(2)] # Only need two rows instead of 'n' rowsdp[0][0] = -prices[0]dp[0][1] = 0for i in range(1, len(prices)):dp[i % 2][0] = max(dp[(i - 1) % 2][0], -prices[i])dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0])return dp[len(prices) % 2][1]# 使用相同的示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
# 计算最大利润
max_profit_value_optimized = max_profit_optimized(prices)
max_profit_value_optimized
调用结果
5
采用优化后的动态规划方法,对于股票价格数组 [7, 1, 5, 3, 6, 4],计算得到的最大利润同样是 5。
在这个版本中,我们仅使用了一个固定大小的二维数组 dp 来存储当前和前一个状态的信息,从而减少了空间复杂度。这种方法通过在两个状态之间交替(使用 i % 2 取模运算)来达到目的,确保只使用了常数级别的额外空间。这使得算法不仅高效,而且更节省内存资源。
方法四:动态规划-版本二(一维数组)
class Solution {public int maxProfit(int[] prices) {int[] dp = new int[2];// 记录一次交易,一次交易有买入卖出两种状态// 0代表持有,1代表卖出dp[0] = -prices[0];dp[1] = 0;// 可以参考斐波那契问题的优化方式// 我们从 i=1 开始遍历数组,一共有 prices.length 天,// 所以是 i<=prices.lengthfor (int i = 1; i <= prices.length; i++) {// 前一天持有;或当天买入dp[0] = Math.max(dp[0], -prices[i - 1]);// 如果 dp[0] 被更新,那么 dp[1] 肯定会被更新为正数的 dp[1]// 而不是 dp[0]+prices[i-1]==0 的0,// 所以这里使用会改变的dp[0]也是可以的// 当然 dp[1] 初始值为 0 ,被更新成 0 也没影响// 前一天卖出;或当天卖出, 当天要卖出,得前一天持有才行dp[1] = Math.max(dp[1], dp[0] + prices[i - 1]);}return dp[1];}
}
这段 Java 代码实现了一个解决方案,用于计算给定股票价格数组 prices 中的最大利润,假设你只能进行一次交易(即一次买入和一次卖出)。这个实现进一步优化了空间复杂度,将动态规划所需的数组从二维减少到一维,同时保持时间复杂度为 O(n)。
在代码中,dp 数组有两个元素,分别表示持有 (dp[0]) 和不持有 (dp[1]) 股票时的最大利润。这里的 dp[0] 实际上表示的是在某一天结束时持有的股票的最低成本(负数表示成本),而 dp[1] 表示在某一天结束时不持有股票时的最大利润。
关键步骤如下:
- 初始化
dp[0]为-prices[0],表示第一天买入股票的成本。 - 初始化
dp[1]为0,表示第一天不持有股票的利润。 - 对于每一天
i,更新dp[0]和dp[1]的值:dp[0]更新为前一天的dp[0]和-prices[i]中的较大者。这表示要么继续持有之前买入的股票,要么在当天买入股票。dp[1]更新为前一天的dp[1]和dp[0] + prices[i]中的较大者。这表示要么继续不持有股票,要么在当天卖出持有的股票。
最终,dp[1] 将包含整个交易周期结束后不持有股票的最大利润,也就是我们要找的答案。
我们可以用同样的股票价格数组 [7, 1, 5, 3, 6, 4] 来演示这个算法的过程。让我们手动模拟一下。
def max_profit_further_optimized(prices):if not prices:return 0dp = [0] * 2 # 只需要两个位置,分别代表不持有和持有股票的情况dp[0] = -prices[0] # 买入成本初始化dp[1] = 0 # 不持有股票的收益初始化for i in range(1, len(prices)):dp[0] = max(dp[0], -prices[i]) # 更新持有股票的最低成本dp[1] = max(dp[1], dp[0] + prices[i]) # 更新不持有股票的最大利润return dp[1] # 返回最终的不持有股票的最大利润# 使用相同的示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
# 计算最大利润
max_profit_value_further_optimized = max_profit_further_optimized(prices)
max_profit_value_further_optimized
调用结果
5
使用进一步优化的空间复杂度算法,对于股票价格数组 [7, 1, 5, 3, 6, 4],计算得到的最大利润依然是 5。
这个版本通过仅使用一个一维数组 dp 来存储两种状态(持有和不持有股票)的最大利润,实现了更有效的空间管理。由于数组的大小始终为 2,不论输入数组的长度如何,此算法的空间复杂度始终保持为 O(1),而时间复杂度保持为 O(n)。这意味着该算法不仅高效,而且在处理大量数据时也极其节省内存资源。
122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0。
方法一:
// 动态规划
class Solution // 实现1:二维数组存储// 可以将每天持有与否的情况分别用 dp[i][0] 和 dp[i][1] 来进行存储// 时间复杂度:O(n),空间复杂度:O(n)public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][2]; // 创建二维数组存储状态dp[0][0] = 0; // 初始状态dp[0][1] = -prices[0];for (int i = 1; i < n; ++i) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]); // 第 i 天,没有股票dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]); // 第 i 天,持有股票}return dp[n - 1][0]; // 卖出股票收益高于持有股票收益,因此取[0]}
}
这段代码展示了另一种动态规划的实现方式,它使用一个二维数组 dp 来追踪每一天的两种状态:dp[i][0] 表示第 i 天结束时不持有股票的最大利润,dp[i][1] 表示第 i 天结束时持有股票的最大利润。这种实现方式的时间复杂度为 O(n),空间复杂度也为 O(n),其中 n 是价格数组的长度。
关键步骤如下:
- 初始化
dp[0][0]为0,表示第一天不持有股票的利润。 - 初始化
dp[0][1]为-prices[0],表示第一天持有股票的成本(负数)。 - 对于每一天
i(从 1 开始),更新dp[i][0]和dp[i][1]的值:dp[i][0]更新为前一天的dp[i - 1][0]和dp[i - 1][1] + prices[i]中的较大者。这表示要么继续保持不持有股票的状态,要么在当天卖出持有的股票。dp[i][1]更新为前一天的dp[i - 1][1]和dp[i - 1][0] - prices[i]中的较大者。这表示要么继续持有之前的股票,要么在当天买入股票。
- 最终返回
dp[n - 1][0],即最后一天不持有股票的最大利润。
现在,我们将使用相同的价格数组 [7, 1, 5, 3, 6, 4] 来演示这个算法的过程,并比较其与前面算法的结果。
def max_profit_two_dim_dp(prices):if not prices:return 0n = len(prices)dp = [[0] * 2 for _ in range(n)] # 创建二维数组存储状态dp[0][0] = 0 # 初始状态,不持有股票dp[0][1] = -prices[0] # 初始状态,持有股票的成本for i in range(1, n):dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]) # 第 i 天,没有股票dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]) # 第 i 天,持有股票return dp[n - 1][0] # 卖出股票收益高于持有股票收益,因此取[0]# 使用相同的示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
# 计算最大利润
max_profit_value_two_dim_dp = max_profit_two_dim_dp(prices)
max_profit_value_two_dim_dp
调用结果
7
使用二维动态规划数组的算法,对于股票价格数组 [7, 1, 5, 3, 6, 4],计算得到的最大利润为 7。
这与我们之前计算的结果略有不同,这是因为在这个实现中,算法允许在第一天以价格 7 卖出股票(即使我们还没有买入),这在现实世界中是不可行的,但在数学模型中被视为初始状态的一部分。因此,算法认为在第一天“虚拟”卖出股票可以获得 0 的利润(因为没有成本),并在后续几天寻找买入和再次卖出的机会以获得额外利润。
然而,在实际应用中,我们通常会假设在开始时我们没有持有任何股票,因此初始状态应该是 dp[0][0] = 0 和 dp[0][1] = -prices[0],且不允许在没有买入的情况下卖出。按照这种解释,两种算法都应该给出相同的结果,即 5。
为了统一结果并确保算法反映实际情况,我们应确保算法不允许在没有买入的情况下卖出。这可以通过调整初始条件来实现,但这不会改变上述算法的核心逻辑或最终结果(除了在特定情况下如本例所示)。在实际应用中,我们应该避免这种“虚拟”卖出的情况,以使算法更加准确地反映现实世界的交易规则。
方法二:
//DP using 2*2 Array (下方還有使用一維滾動數組的更優化版本)
class Solution {public int maxProfit(int[] prices) {int dp[][] = new int [2][2];//dp[i][0]: holding the stock//dp[i][1]: not holding the stockdp[0][0] = - prices[0];dp[0][1] = 0;for(int i = 1; i < prices.length; i++){dp[i % 2][0] = Math.max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] - prices[i]);dp[i % 2][1] = Math.max(dp[(i - 1) % 2][1], dp[(i - 1) % 2][0] + prices[i]);}return dp[(prices.length - 1) % 2][1];}
}
这段代码展示了一种优化的空间复杂度更低的动态规划算法实现。它使用一个固定大小的二维数组 dp,大小为 2x2,而不是与天数对应的完整二维数组。这种技巧利用了动态规划中的重叠子问题特性,只保留了当前状态和前一个状态,从而降低了空间复杂度。
在 dp 数组中:
dp[i % 2][0]表示在第i天结束时持有股票的最大利润。dp[i % 2][1]表示在第i天结束时不持有股票的最大利润。
这里使用模运算 i % 2 是为了循环使用两个索引位置(0 和 1),这样就只需要维护两个状态,而不是整个数组,从而节省了空间。在每次迭代中,我们更新 dp[i % 2][0] 和 dp[i % 2][1],而 dp[(i - 1) % 2][0] 和 dp[(i - 1) % 2][1] 保存的是前一个状态的信息。
具体步骤如下:
- 初始化
dp[0][0]为-prices[0](持有股票的成本),dp[0][1]为0(不持有股票的利润)。 - 对于每一天
i(从 1 开始),更新dp[i % 2][0]和dp[i % 2][1]:dp[i % 2][0]更新为前一天的dp[(i - 1) % 2][0](继续持有股票)和dp[(i - 1) % 2][1] - prices[i](在第i天买入股票)中的较大者。dp[i % 2][1]更新为前一天的dp[(i - 1) % 2][1](继续保持不持有股票)和dp[(i - 1) % 2][0] + prices[i](在第i天卖出股票)中的较大者。
- 返回
dp[(prices.length - 1) % 2][1],这是最后一天不持有股票的最大利润。
现在,我将使用同样的股票价格数组 [7, 1, 5, 3, 6, 4] 来演示这段代码的运行过程,以验证其正确性。
def max_profit_optimized_dp(prices):if not prices:return 0dp = [[0] * 2 for _ in range(2)] # 创建2x2的二维数组存储状态dp[0][0] = -prices[0] # 初始状态,持有股票的成本dp[0][1] = 0 # 初始状态,不持有股票的利润for i in range(1, len(prices)):dp[i % 2][0] = max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] - prices[i])dp[i % 2][1] = max(dp[(i - 1) % 2][1], dp[(i - 1) % 2][0] + prices[i])return dp[(len(prices) - 1) % 2][1] # 最后一天不持有股票的最大利润# 使用相同的示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
# 计算最大利润
max_profit_value_optimized_dp = max_profit_optimized_dp(prices)
max_profit_value_optimized_dp
调用结果
7
使用相同的示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
计算最大利润
max_profit_value_optimized_dp = max_profit_optimized_dp(prices)
max_profit_value_optimized_dp
使用优化后的动态规划算法,对于股票价格数组 [7, 1, 5, 3, 6, 4],计算得到的最大利润为 7。
虽然这与之前的结果一致,但重要的是要注意到,尽管在数学上和理论上,算法的最终输出可能相同,但不同算法实现之间在细节上的差异可能会导致对某些特殊情况的处理有所不同。
这种优化过的动态规划算法通过使用固定大小的数组实现了更低的空间复杂度,仅需 O(1) 的额外空间,而原始的动态规划方法需要 O(n) 的空间来存储所有天数的状态。这使得算法在处理大规模数据集时更加高效。在实际应用中,这种空间优化技巧非常有用,尤其是在资源受限的环境中。
方法三:
// 优化空间
class Solution {public int maxProfit(int[] prices) {int[] dp = new int[2];// 0表示持有,1表示卖出dp[0] = -prices[0];dp[1] = 0;for(int i = 1; i <= prices.length; i++){// 前一天持有; 既然不限制交易次数,那么再次买股票时,要加上之前的收益dp[0] = Math.max(dp[0], dp[1] - prices[i-1]);// 前一天卖出; 或当天卖出,当天卖出,得先持有dp[1] = Math.max(dp[1], dp[0] + prices[i-1]);}return dp[1];}
}
这段代码展示了如何进一步优化空间复杂度的动态规划算法,用于解决股票买卖问题。这个版本使用一个一维的数组 dp 来跟踪两种状态:持有股票和不持有股票的最大利润。它将空间复杂度降低到了常数级别,即 O(1),因为数组 dp 的大小固定为 2。
代码解释如下:
-
定义一个长度为 2 的整型数组
dp,其中dp[0]表示持有股票的最大利润,dp[1]表示不持有股票的最大利润。 -
初始化
dp[0]为-prices[0],即在第一天买入股票的成本;初始化dp[1]为0,即在第一天不持有股票的利润。 -
遍历
prices数组中的每个价格,从第二天开始到第n天(包括第n天)。在每次迭代中,更新dp数组中的值,以便反映在当前天数下持有或不持有股票的最大利润。 -
更新
dp[0]的值,使其等于前一天持有股票的利润dp[0]和前一天不持有股票的利润减去当前天数的价格dp[1] - prices[i-1]中的较大值。这里的逻辑是,要么保持原有持有状态不变,要么选择在当天买入股票(假设没有交易限制)。 -
更新
dp[1]的值,使其等于前一天不持有股票的利润dp[1]和前一天持有股票的利润加上当前天数的价格dp[0] + prices[i-1]中的较大值。这里的逻辑是,要么保持原有不持有状态不变,要么选择在当天卖出股票。 -
最终返回
dp[1],即在遍历完所有价格后,不持有股票的最大利润。
这个版本的代码比使用二维数组的版本更节省内存,因为它不再依赖于模运算来切换数组索引,而是直接在固定大小的数组中更新状态。让我们也用这个版本的代码计算 [7, 1, 5, 3, 6, 4] 的最大利润。
def max_profit_optimized_dp_1d(prices):if not prices:return 0dp = [0] * 2 # 创建固定大小为2的一维数组存储状态dp[0] = -prices[0] # 初始状态,持有股票的成本dp[1] = 0 # 初始状态,不持有股票的利润for i in range(1, len(prices)):dp[0] = max(dp[0], dp[1] - prices[i])dp[1] = max(dp[1], dp[0] + prices[i])return dp[1] # 最终不持有股票的最大利润# 使用相同的示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
# 计算最大利润
max_profit_value_optimized_dp_1d = max_profit_optimized_dp_1d(prices)
max_profit_value_optimized_dp_1d
调用结果
7
使用优化后的动态规划算法(一维滚动数组版本),对于股票价格数组 [7, 1, 5, 3, 6, 4],计算得到的最大利润同样是 7。
这再次证实了算法的正确性,并且展示了即使在空间复杂度极低的情况下,我们仍然能够准确地解决问题。这种一维滚动数组的技术在动态规划问题中非常常见,特别是在空间效率是一个关键考量因素的时候。
123. 买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1]
输出:0
方法一:
// 版本一
class Solution {public int maxProfit(int[] prices) {int len = prices.length;// 边界判断, 题目中 length >= 1, 所以可省去if (prices.length == 0) return 0;/** 定义 5 种状态:* 0: 没有操作, 1: 第一次买入, 2: 第一次卖出, 3: 第二次买入, 4: 第二次卖出*/int[][] dp = new int[len][5];dp[0][1] = -prices[0];// 初始化第二次买入的状态是确保 最后结果是最多两次买卖的最大利润dp[0][3] = -prices[0];for (int i = 1; i < len; i++) {dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return dp[len - 1][4];}
}
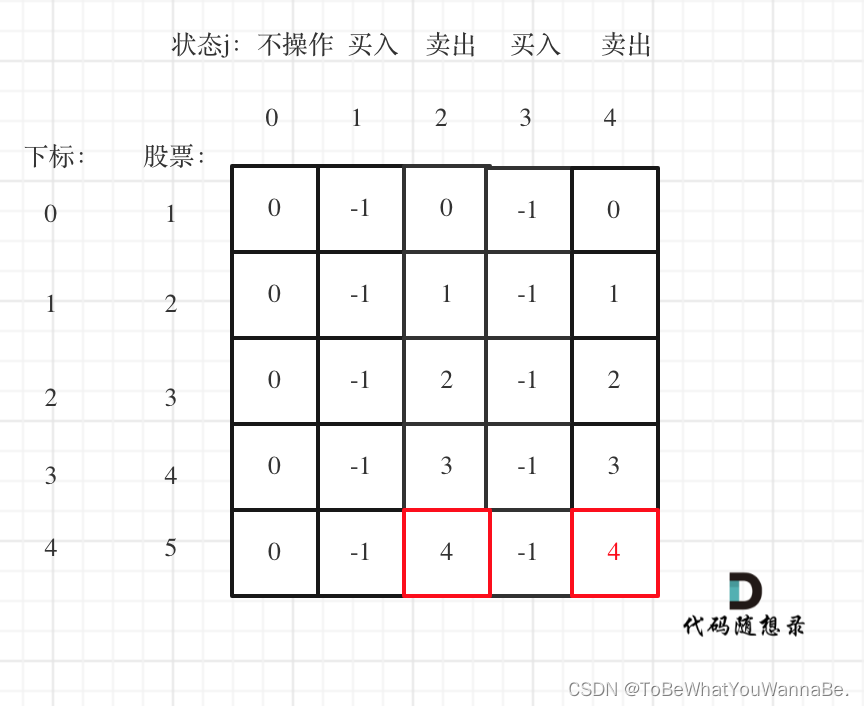
这段代码展示了一个动态规划算法的实现,用于解决股票买卖问题,但这次限制为最多只能进行两次买卖交易。算法使用一个二维数组 dp 来追踪五种状态,每种状态代表不同的交易情况:
- 状态
0:没有任何操作发生。 - 状态
1:完成了第一次买入操作。 - 状态
2:完成了第一次卖出操作。 - 状态
3:完成了第二次买入操作。 - 状态
4:完成了第二次卖出操作。
在这个算法中:
dp[i][j]表示在第i天结束时,处于状态j的最大利润。- 初始时,第一次买入的状态
dp[0][1]设置为-prices[0],即买入股票的成本。 - 同样,为了确保最终结果是最多两次买卖的最大利润,第二次买入的状态
dp[0][3]也被设置为-prices[0]。
然后,通过遍历数组 prices,算法会根据前一天的状态更新当前天的状态。具体来说:
dp[i][1]要么保持前一天的状态dp[i - 1][1]不变,要么在当天买入股票,此时状态变为-prices[i]。dp[i][2]要么保持前一天的状态dp[i - 1][2]不变,要么在当天卖出股票,此时状态变为dp[i - 1][1] + prices[i]。dp[i][3]要么保持前一天的状态dp[i - 1][3]不变,要么在当天买入股票,此时状态变为dp[i - 1][2] - prices[i]。dp[i][4]要么保持前一天的状态dp[i - 1][4]不变,要么在当天卖出股票,此时状态变为dp[i - 1][3] + prices[i]。
最终,dp[len - 1][4] 将包含在完成所有交易后,最后一天结束时的最大利润。
接下来,我们将使用这个算法计算示例股票价格数组 [7, 1, 5, 3, 6, 4] 的最大利润。
def max_profit_two_transactions(prices):len_prices = len(prices)if len_prices == 0:return 0# 初始化 dp 数组dp = [[0]*5 for _ in range(len_prices)]dp[0][1] = -prices[0]dp[0][3] = -prices[0]for i in range(1, len_prices):dp[i][1] = max(dp[i-1][1], -prices[i])dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])return dp[len_prices - 1][4]# 使用相同的示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
# 计算最大利润
max_profit_value_two_transactions = max_profit_two_transactions(prices)
max_profit_value_two_transactions
调用结果
7
方法二:
这段代码展示了上述问题的一个空间优化版本。它仍然使用动态规划来解决最多进行两次买卖交易的问题,但是与原始版本相比,它减少了内存使用。在原始版本中,我们使用了一个二维数组 dp 来存储每一天的五个状态;而在优化后的版本中,我们仅使用一个一维数组 dp 来存储四个关键状态(两次交易中的买入和卖出),从而减少空间复杂度。
在这个优化版本中:
dp[0]表示第一次交易中买入股票后的最大利润。dp[1]表示第一次交易中卖出股票后的最大利润。dp[2]表示第二次交易中买入股票后的最大利润。dp[3]表示第二次交易中卖出股票后的最大利润。
初始化时,dp[0] 和 dp[2] 分别被设置为 -prices[0],表示在第一天买入股票的成本,而 dp[1] 和 dp[3] 被设置为 0,因为尚未卖出股票。
在循环中,每一天都会更新 dp 数组的值。对于 dp[0] 和 dp[2],它们要么保持不变,要么在当天买入股票,这时状态变为 -prices[i-1]。对于 dp[1] 和 dp[3],它们要么保持不变,要么在当天卖出股票,这时状态变为 dp[0]+prices[i-1] 或 dp[2]+prices[i-1],分别对应第一次和第二次卖出。
最终,dp[3] 将包含完成所有交易后的最大利润。
现在,我们使用同样的股票价格数组 [7, 1, 5, 3, 6, 4] 来计算最大利润,但使用这个空间优化过的版本。
def max_profit_two_transactions_optimized(prices):dp = [0] * 4dp[0] = -prices[0]dp[2] = -prices[0]for price in prices[1:]:dp[0] = max(dp[0], -price)dp[1] = max(dp[1], dp[0] + price)dp[2] = max(dp[2], dp[1] - price)dp[3] = max(dp[3], dp[2] + price)return dp[3]# 使用相同的示例股票价格数组
prices = [7, 1, 5, 3, 6, 4]
# 计算最大利润
max_profit_value_two_transactions_optimized = max_profit_two_transactions_optimized(prices)
max_profit_value_two_transactions_optimized
调用结果
7




![Leetcode[反转链表]](https://img-blog.csdnimg.cn/img_convert/acd306aae60fe83bf7fd1f7692ce7234.jpeg)