法线/凹凸贴图

• 如何让纹理产生更细节的效果，产生凹凸视觉感？
• 解决思路之一：镜面贴图(黑—白）（（diffuse贴图（rgba）），阻止部分表面被照的更亮，但这并不是一个好方案。我们需要模拟深度这样的细节的方式。而非反射效果。
• 是什么使表面被视为完全平坦的表面来照亮？答案是法线向量，第二个解决方案：
• 法线/凹凸贴图（偏蓝色调的纹理）：替代一个面上所有fragment为法线贴图采样，模拟凹凸感，细节获得了极大提升，开销却不大
• 纹理：存储颜色，深度值，模板值，法线向量……

基本概念

• 将法线向量的x、y、z元素储存到纹理中，代替颜色的r、g、b（红，绿，蓝大部分法线指向z轴，所以大部分都为蓝色）元素。
• 用纹理储存法线向量：法线向量的范围在-1到1之间，所以我们先要将其映射到0到1的范围（* 0.5 + 0.5;）：将法线向量变换为像这样的RGB颜色元素，我们就能保存在2D纹理中
• 注意，我们真正使用的法线贴图，是上下颠倒的，OpenGL读取的纹理的y（或V）坐标和纹理通常被创建的方式相反
• 从法线贴图采样的法线颜色从0到1重新映射回-1到1（* 2.0 - 1.0），便能将RGB颜色重新处理成法线

当我们旋转实体，

• 光照看起来完全不对（普通的normal可以*model变换到世界坐标），原因：法线贴图里面的所有法线向量依旧是指向正z方向的
• 为什么要有切线空间？我们也可以针对每个变换，新建特定的法线贴图，但那太麻烦了，需要任意的变换法线朝向，可以复用的法线贴图

  

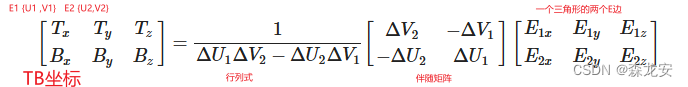
• 切线空间（tangent space）局部坐标系统xyz：
• TBN向量：切线空间的3个向量：tangent切线（右->三角形面）、bitangent副切线（前->三角形面），normal法线（上->法向量）
• 对于一个quad有2个三角形，需要求每个三角形的TBN，每个三角形的每个顶点的TBN都是一样的，有了这个图中的转换公式，就可以求出TB了
• 求TB单位向量：
• 已知顶点坐标（求边E）和纹理坐标（求差U与T方向相同，V与𝐵方向相同），边向量E = 向量1 UT + 向量2VB （向量加法），分解为矩阵xyz3个分量，
• 平滑：
• 通常三角形和三角形之间都会共享顶点。这种情况下开发者通常将每个顶点的法线和切线/副切线等顶点属性平均化，以获得更加柔和的效果。

在glsl中创建mat3 TBN，如何使用它？

• TBN矩阵：切线空间转成世界或视图空间下，从法线贴图采样法线，映射回-1到1，*TBN变换到世界空间
• TBN逆矩阵：世界或视图空间下转成切线空间中
• 注意，这里用到置换函数transpose，而非求逆函数inverse，对于正交矩阵（每个轴既是单位向量同时相互垂直）的一大属性是一个正交矩阵的置换矩阵与它的逆矩阵相等。因为逆矩阵的求得比求置换开销大；结果却是一样的。
• 第二种方法看似要做的更多，为何还第二种方法呢？
• uniform变量（对本shader属于全局的，唯一的，所以每次每个片段运行都是一致的），完全可以在vertex去计算，顶点着色器通常比像素着色器运行的少。这是一个极佳的优化。对于法线每个顶点运行fragment shader都是不同的，采样的都是不一致的，所以必须放在fragment shader中

为模型应用法线贴图

• 图中：可以看到应用了Normal_Texture->TBN后的model，显示的更加立体，凹凸感。
• assimp库当ReadFile（）调用aiProcess_CalcTangentSpace来加载场景scene时，Assimp会为每个加载的顶点计算出柔和的切线和副切线向量
• 通过mesh->mTangents[i].获取切线空间
• loadMaterialTextures时需要aiTextureType_NORMAL加载法线贴图
• //
• 格拉姆-施密特正交化： (不必花费太多性能开销的情况下稍稍提升画质表现)
• 更大的网格上计算切线向量的时候，它们往往有很大数量的共享顶点,当法向贴图应用到这些表面时将切线向量平均化时通常能获得更好更平滑的结果。就是TBN向量可能会不能互相垂直，
• 重正交化：T = normalize(T - dot(T, N) * N)

矩阵：

• 矩阵乘法：A(mx) * B(yn) = C(mn),注意：xy必须相等，才可以相乘
• 行列式determinant：计算方法（（基本算法，其余还包括：代数余子式，等价转化法，逆序数法……）
  • 对角线法：斜对角线（左下右上）每条相乘后相加  - 斜对角线（左上右下）每条相乘后相加 
  • 作用：应用于求逆矩阵的过程
• 转置transpose A^T：横读竖写
• 伴随矩阵A*：
  • 分量aij的余子式Mij：对于矩阵A，将i行j列划去后，剩余的分量按照原顺序排列得到的n-1阶矩阵，所确定的行列式
  • 分量aij的代数余子式Aij：符号（-1^i+j) * Mij
  • A的伴随矩阵A*:由各分量aij的代数余子式Aij构成
  • 计算过程：
    • 首先求解每个分量的Mij
    • 再计算符号*Mij
  • 应用：线性方程组：把每个系数写为矩阵中的对应分量……
  • 作用：应用于求逆矩阵的过程
• 逆矩阵inverse A^-1：
  • 和倒数原理一样，x * 1/x = 1； A * A^-1（因为矩阵不能被除） = 单位矩阵(对角线上的数字都是1，其他地方都是0)
  • 如何计算一个矩阵的逆矩阵A^-1？（基本算法，其余还包括初等变换……）
    • 待定系数法：新建矩阵X，对应分量写成等式 == 单位矩阵的对应分量，求系数，即逆矩阵
    • 伴随矩阵：  伴随矩阵  / 行列式 （float） (或 * 1/行列式）
  • 普通除法：已知a * x = b,求x，x = b / a == b * (1/a) ->应用于矩阵
  • 矩阵：A * X = B，我们可以通过 （B/A->）B * A^-1，求出X矩阵（相当于除法的作用）