摘要 计算机的错误计算(二十二)阐明:对于结果应该为 0的算式,即使增加计算精度,也得不出0. 针对 ,本节给出一种解决方案。
计算机的错误计算(十九)展示了计算机对 的错误计算:本应该为 0的算式的结果不为0; 计算机的错误计算(二十二)说明:即使增加计算精度,也得不出0;计算机的错误计算(二十)与(七)指出,错误结果主要是由 exp(x) 函数的错误计算所引起,并且其结果中有约 3位错误数字。
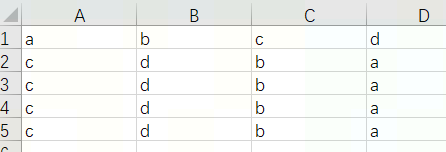
既然知道错误数字是 3位,那么先去掉它们,再相减,就得出了0.
请看下面在数学软件 Maple 下的计算过程:

假设有效位数为16位。那么,首先在 16+3=19位下计算减数,然后获得其 16位的值(舍弃后 3位),再在 16位下做减法。这样就得到了正确结果0.
当然,这种计算方法只有在可任意设置精度的环境下,才能得以实施。 如果仅有有限的几个精度,那不太行。另外,不要小瞧这种小儿科的计算方法,有时,不得不用它。
再者,若算式比较复杂,那么这种方法未必奏效。
对于复杂一点的算式,如何获得其准确值,是一个极极极具挑战性的难题(您想想,一元二次方程的那么简单的求根公式的计算都属于挑战性的难题,参见计算机的错误计算(四))。这也正是这些文字系列存在的必要性。











![[VN2020 公开赛]strangeCpp](https://i-blog.csdnimg.cn/direct/b0d70ef3625e4bc190ec2134fe972e0b.png)
