目录

Saturated Regression Model

Regression as Variance Weighted Average

---

Saturated Regression Model

还记得我在本章开头强调回归和条件平均值之间的相似性吗？我向你展示了使用二元干预进行回归与比较干预组和对照组的平均值是完全一样的。现在，由于虚拟变量是二进制列，因此相似之处同样适用于此。如果你把条件随机实验数据交给一个不像你一样精通回归的人，他们的第一反应可能是简单地按信用分数 credit_score1_buckets 对数据进行分割，然后分别估计每组的效果：

 def regress(df, t, y):return smf.ols(f"{y}~{t}", data=df).fit().params[t]effect_by_group = (risk_data_rnd.groupby("credit_score1_buckets").apply(regress, y="default", t="credit_limit"))effect_by_group

这将得出各组的效果，这意味着您还必须决定如何对它们进行平均。一个自然的选择是加权平均，其中的权重是每个组的大小：

 group_size = risk_data_rnd.groupby("credit_score1_buckets").size()ate = (effect_by_group * group_size).sum() / group_size.sum()

当然，您也可以通过运行所谓的饱和模型来进行完全相同的回归。您可以将虚拟变量与干预进行交互，从而得到每个虚拟变量定义组的效应。在本例中，由于去除了第一个虚拟组，与 credit_limit 相关的参数实际上代表了被省略的虚拟组 sb_100 的效果。它与上文针对信用评分 1_bucketsearlier 组 0 至 200 的估计值完全相同：-0.000071：

 model = smf.ols("default ~ credit_limit * C(credit_score1_buckets)",data=risk_data_rnd).fit()model.summary().tables[1]

交互参数的解释与第一组（省略）的效果有关。因此，如果将与 credit_limit 相关的参数与其他交互项相加，就可以看到通过回归估算出的各组效应。这与估计每个组的影响完全相同： 

  (model.params[model.params.index.str.contains("credit_limit:")]+ model.params["credit_limit"]).round(9)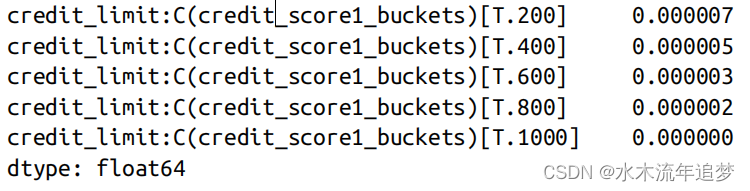

按组别绘制该模型的预测图还会显示，现在就好像是在为每个组别拟合单独的回归。每条线不仅截距不同，斜率也不同。此外，在其他条件相同的情况下，饱和模型的参数（自由度）更多，这也意味着方差更大。如果您看下面的图，就会发现一条斜率为负的线，这在这种情况下是不合理的。不过，这个斜率在统计学上并不显著。这可能只是由于该组样本较少而产生的噪音： 

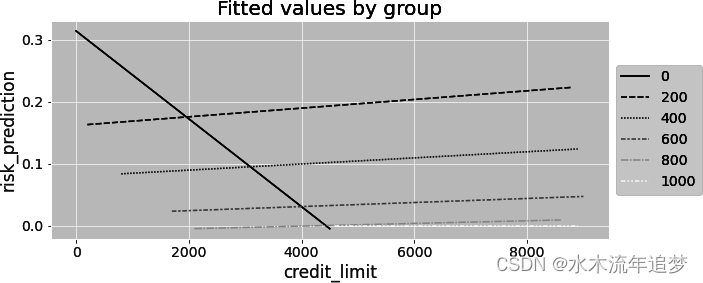
Regression as Variance Weighted Average

但是，如果饱和回归和按组别计算效应的结果完全相同，那么你可能会问自己一个非常重要的问题。如果运行 default ~ credit_limit + C(credit_score1_buckets)模型，且不包含交互项，则会得到单一效应：只有一个斜率参数。重要的是，如果你回头看，这个效应估计值与你通过估计每个组的效应并用组大小作为权重求平均值得到的效应估计值是不同的。因此，回归是以某种方式将不同组别的效应结合起来。而它的方法并不是样本量加权平均。那么它是什么呢？

要回答这个问题，最好的办法还是使用一些非常说明问题的模拟数据。在这里，让我们模拟两个不同小组的数据。第 1 组的人数为 1000 人，平均干预效果为 1；第 2 组的人数为 500 人，平均干预效果为 2。此外，第 1 组的干预标准差为 1，第 2 组的干预标准差为 2：

 np.random.seed(123)# std(t)=1t1 = np.random.normal(0, 1, size=1000)df1 = pd.DataFrame(dict(t=t1,y=1*t1, # ATE of 1g=1, ))# std(t)=2t2 = np.random.normal(0, 2, size=500)df2 = pd.DataFrame(dict(t=t2,y=2*t2, # ATE of 2g=2,))df = pd.concat([df1, df2])df.head()

如果你分别估计每一组的效果，并以组大小为权重取结果平均值，你得到的ATE约为1.33,1 * 1000 + 2 * 500 /1500：

effect_by_group = df.groupby("g").apply(regress, y="y", t="t")ate = (effect_by_group *df.groupby("g").size()).sum() / df.groupby("g").size().sum()ate1.333333333333333

但是，如果在控制组别的情况下对 y 对 t 进行回归，结果就大不相同了。现在，综合效应更接近于第 2 组的效应，尽管第 2 组的样本只有第 1 组的一半：

 model = smf.ols("y ~ t + C(g)", data=df).fit()model.paramsIntercept 0.024758C(g)[T.2] 0.019860t 1.625775dtype: float64

其原因在于回归并不是通过使用样本量作为权重来合并组间效应。相反，它使用的权重与各组干预的方差成正比。回归法更倾向于治疗方法差异较大的组。这初看起来可能很奇怪，但仔细想想，就很有道理了。如果干预方法在组内变化不大，你怎么能确定其效果呢？如果治疗方法变化很大，它对干预结果的影响就会更加明显。

总而言之，如果你有多个组，而每个组内的干预治疗都是随机的，那么条件性原则就说明，效果是每个组内效果的加权平均值：

根据方法的不同，您将有不同的权重。通过回归，，但您也可以选择手动加权组效应使用样本量作为权重：