一、PID控制器的设计

1.PID控制原理图：

PID控制其结构框图如下图所示：

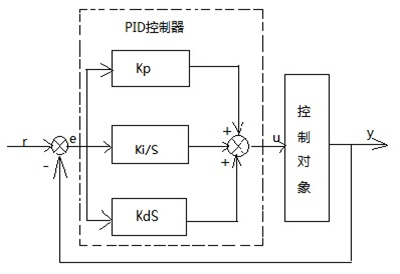
图1：PID控制器结构框图

2.PID控制器传递函数的一般表达式

PID控制器传递函数的一般表达形式为：

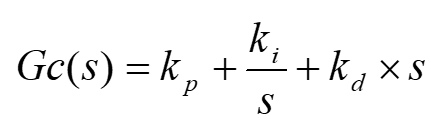
其中kp为比例增益；ki为积分增益；kd为微分增益。

调整PID参数，以满足系统要求，从而使被控对象有更优良的动态响应和静态响应。

比例环节：根据偏差量成比例的调节系统控制量，以此产生控制作用，减少偏差。比例系数的作用是增加系统响应的速度，比例系数越大，系统响应越快，但系统容易产生超调，比例系数过小，会影响系统调节的精度，系统响应时间变长，系统的动态响应变差。

积分环节：用于消除静差，提高系统的无差度，积分时间常数决定着积分环节作用的强度，但是积分作用过强的话会影响系统的稳定性。

微分环节：根据偏差量的变化趋势来调节系统控制量，在偏差信号发生较大变化之前，提早引入一个校正信号，起到加快系统动作速度，减少调节时间的作用，调节微分参数需要注意微分作用太强可能会引起系统振荡。

二、模糊PID控制器的设计

1．模糊控制原理图

模糊控制器结构框图如下图所示：

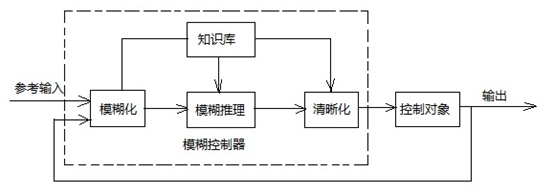
图3：模糊控制器结构框图

上面为模糊控制器的原理图，实际上模糊控制器的输出并非真正的控制信号，而是作为PID的参数。所以完整的模糊PID控制器框图应该需要包含PID控制的部分，如下图所示：

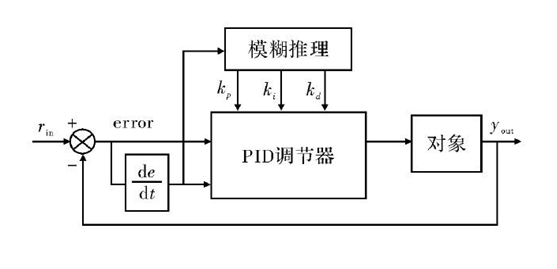
其中模糊推理部分即上面的模糊控制器，PID调节器才是真正起作用的控制器，而模糊控制器的作用是在线实时调整PID参数。

2．模糊控制器传递函数一般表达形式

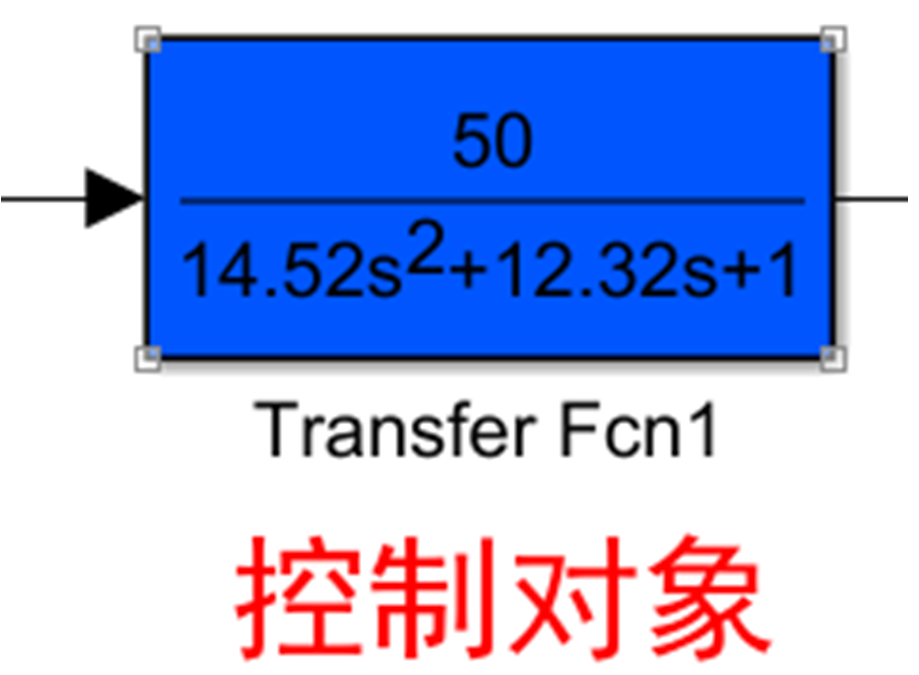
一个典型工业过程通常可以等效为二阶系统加上一个非线性环节（如纯滞后），给出如下经典控制对象传递函数的一般形式：

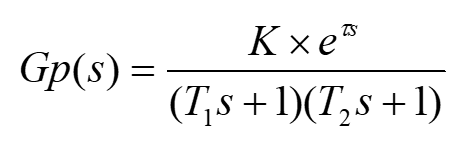
其中模糊控制规则是模糊控制器的核心，是设计控制系统的主要内容。

一个基本模糊控制器主要有三个功能：

（1）模糊化：把精确量（如偏差e和偏差变化ec）转化为相应的模糊量（E、EC）；

（2）模糊推理：按总结的语言规则（模糊控制规划表）进行模糊推理；

（3）模糊判决：把推理结果（U）从模糊量转化为可以用于实际控制的精确量（u）。

模糊规则是由一系列的模糊条件语句组成的，即由许多模糊蕴含关系构成。这些条件语句是推理的出发点和得到的正确结论的根据和基础。每条模糊条件语句都给出模糊蕴含关系，即一条控制规则。若有n条规则，就把它们表达的n个模糊蕴含关系(i=l，2，⋯，n)做并运算，构成系统总的模糊蕴含关系：

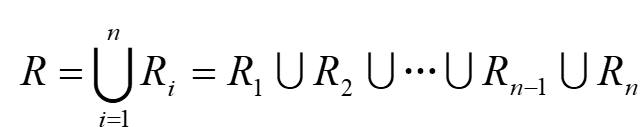
三、系统仿真

本文采用的传递函数为：

用Simulink工具建立由PID控制器组成的系统仿真模型如下图所示，其中比例增益Kp取值0.04，积分增益取值0.03，微分增益取值1.2。选用的输入是单位阶跃信号。

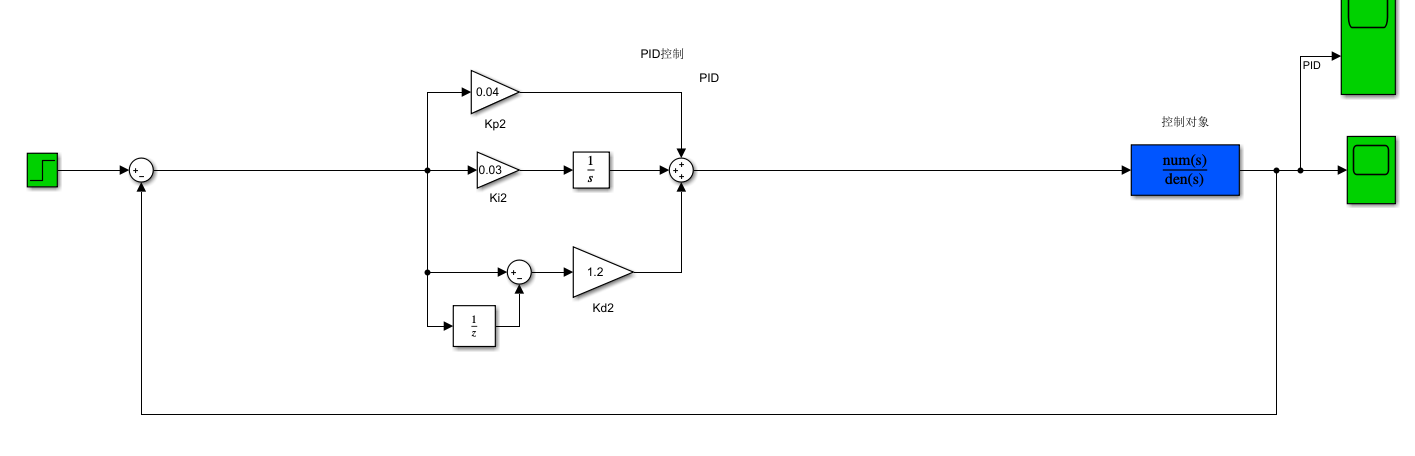
图4：Simulink的PID控制器仿真图

设计模糊PID控制器的主要步骤为：

1. 选择偏差e、偏差变化ec和输出的模糊语言变量为E、EC和Kp,Ki,Kd。根据e、ec和PID参数实际的基本论域，设定E、EC都为[-3,3]，Kp为[-0.3,0.3]，Ki为[-0.06,0.06]，Kd为[-3,3]。模糊控制器前后的GAIN模块为比例因子，可将输出输出转换到论域范围。

2. 选取E、EC和PID参数的各语言变量值：正大为PB，正中为PM，正小为PS，为零为E，负小为NS，负中为NM，负大为NB，它们各自在论域上的模糊子集隶属度函数均为三角形。

3. 选择一种模糊判决方法，将控制量由模糊量变为精确量，这个过程叫做“去模糊化”，这里采用的是“面积平分法”。

用Simulink工具建立由模糊控制器组成的系统仿真模型如下图所示：

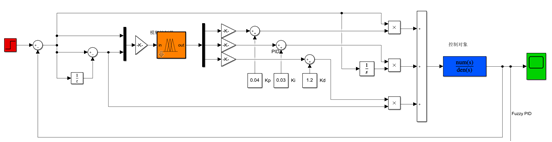
图5：Simulink的模糊PID控制器仿真图

 语言值的隶属函数选择三角形的隶属度函数如下面三幅图所示：

（1）E的隶属度函数：

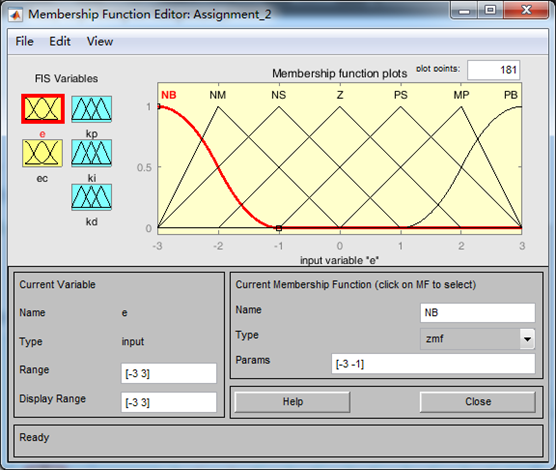
（2）EC的隶属度函数：

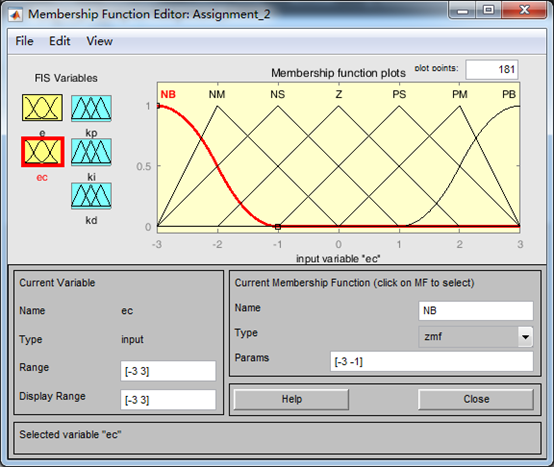
（3）PID参数（即Kp,Ki,Kd）的隶属度函数

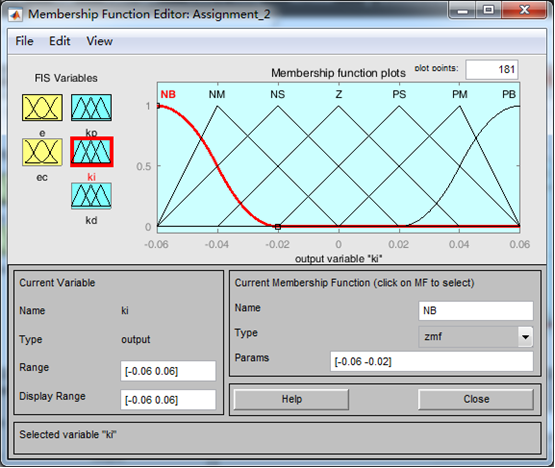
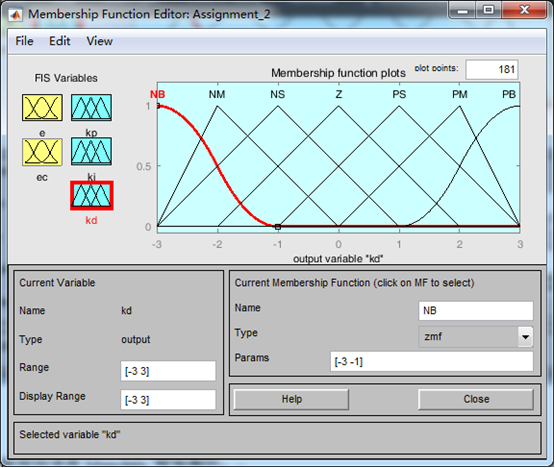
控制规则选用Mamdain 控制规则；

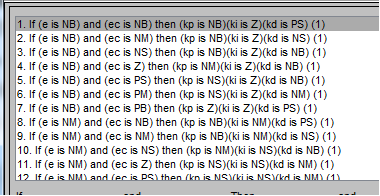
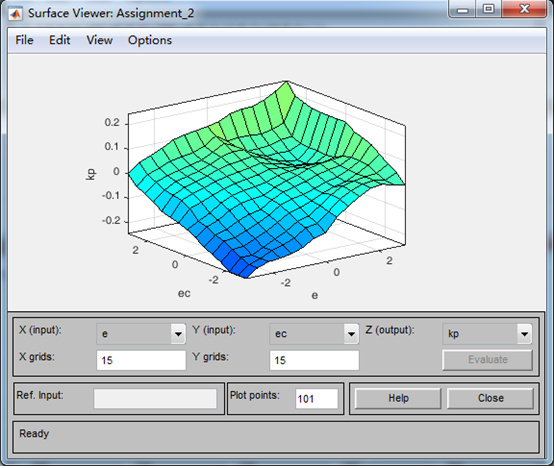
 将规则输入到编辑器中（如图8所示）一共有7×7=49条规则，输入后可以在编辑器中的Rule Viewer（如图9所示）和Surface Viewe（如图10所示）r中查看对具体输入的模糊推理及输出情况,输入各种不同的数据,查看模糊推理情况及输出数据。也可以用于检查，看自己输入的规则和有没有错误。

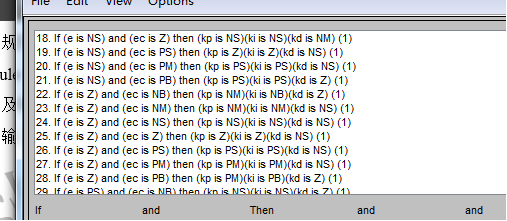
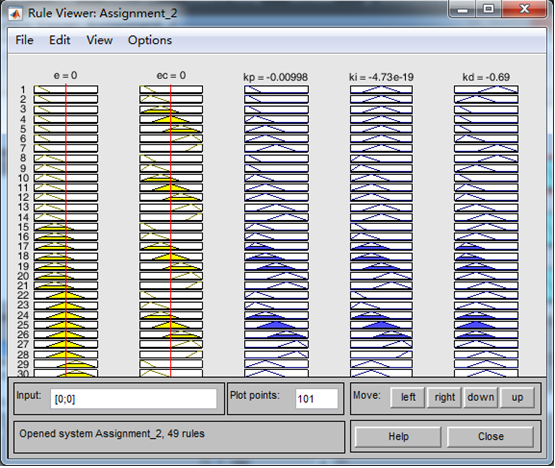
编辑器中的Surface Viewer：

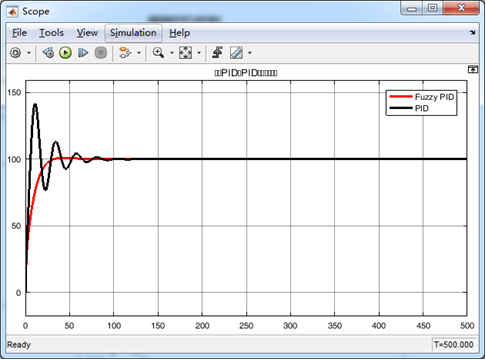
实验得到的结果图形如下所示：

四、下载链接：