机器学习（五） -- 监督学习（6） --逻辑回归

系列文章目录及链接

上篇：机器学习（五） -- 监督学习（5） -- 线性回归2
下篇：机器学习（五） -- 监督学习（7） --SVM1

前言

tips：标题前有“***”的内容为补充内容，是给好奇心重的宝宝看的，可自行跳过。文章内容被“文章内容”删除线标记的，也可以自行跳过。“！！！”一般需要特别注意或者容易出错的地方。

本系列文章是作者边学习边总结的，内容有不对的地方还请多多指正，同时本系列文章会不断完善，每篇文章不定时会有修改。

由于作者时间不算富裕，有些内容的《算法实现》部分暂未完善，以后有时间再来补充。见谅！

文中为方便理解，会将接口在用到的时候才导入，实际中应在文件开始统一导入。

一、通俗理解及定义

1、什么叫逻辑回归（What）

逻辑回归=线性回归+sigmoid函数

逻辑回归（Logistic Regression）简单来讲，就是找到一条直线将一个二分类数据划分开。

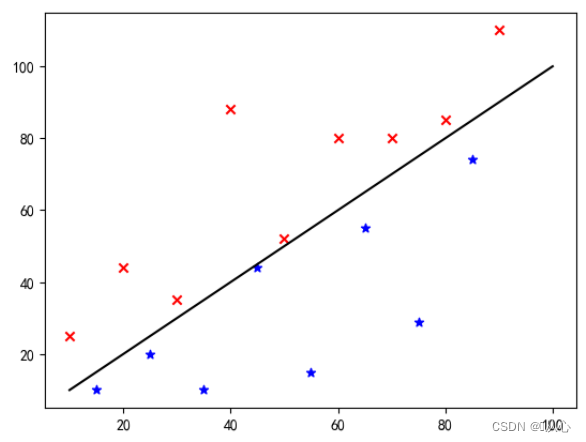
2、逻辑回归的目的（Why）

解决二分类问题，通过属于某个类别的概率值来判断是否属于某个类别，并且这个类别默认标记为1(正例)，另外的一个类别会标记为0(反例)。

3、如何找到这条线（How）

其实这和线性回归步骤类似，其中差别在于“检查模型拟合效果”和“调整模型位置角度”使用的方法有所不同。

随机画一条直线，作为初始的直线
检查一下它的拟合效果，
如果不是最好的（达到阈值），就调整直线位置和角度
重复第2、3步，直到最好效果（到达设定的阈值），最终就是我们想要的模型。

需要用一个函数（sigmoid函数），对于输入的数据都将其映射到0-1之间，并且如果函数值大于0.5，就判定为1，否则属于0。这样就可以转换为概率表示。

二、原理理解及公式

1、感知机

1.1、问题描述

以图片分类为例，将图片分为纵向和横向

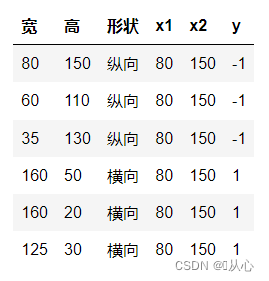
把这些数据通过图上展示就是这样，为了将图中不同颜色（不同类别）的点分开，我们画这样一条线。这次分类的目的就是为了找到这样一条线。

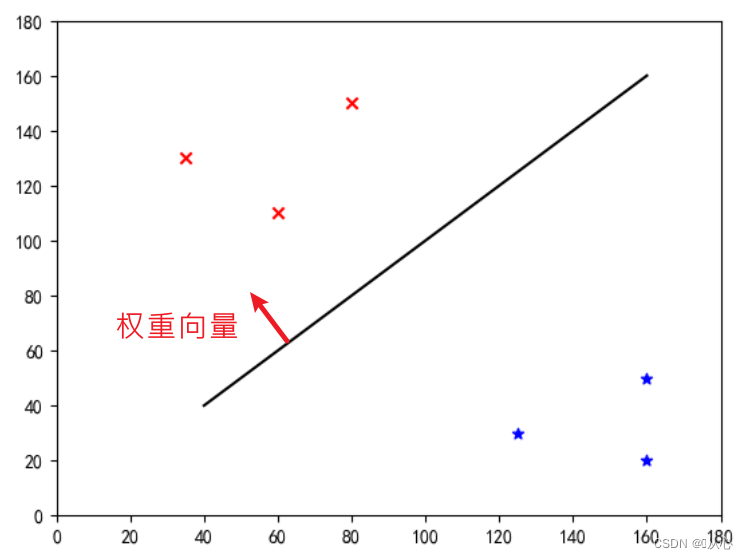
这是一条“使权重向量成为法线向量的直线”（让权重向量与直线垂直）

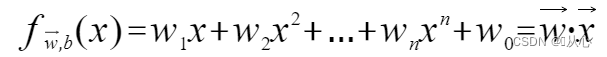
w即为权重向量；使其成为法线向量的的直线，即使

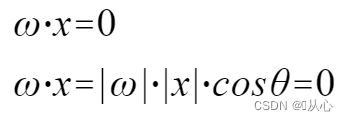
1.2、感知机模型

接受多个值后将每个值与各自权重相乘，最后输出总和的模型。

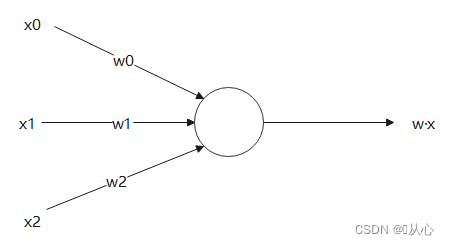
1.3、判别函数

内积是衡量向量之间相似程度的指标，结果为正说明相似，为0则垂直，为负则说明不相似。

用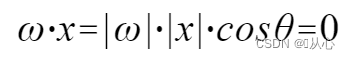更好理解，因为|w|与|x|都为正数，所以决定内积符号的是cosθ，即小于90度为相似，大于90度为不相似，即

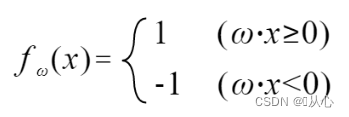
1.4、参数估计（权重更新表达式）

若与原标签值相等，则权重向量不更新，若与原标签值不等，则用向量相加为权重向量更新。

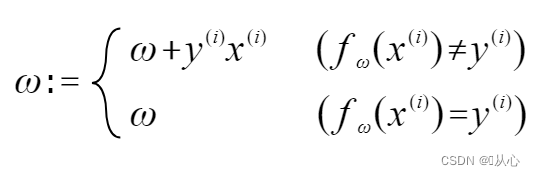
如图所示，若与原标签不等，则

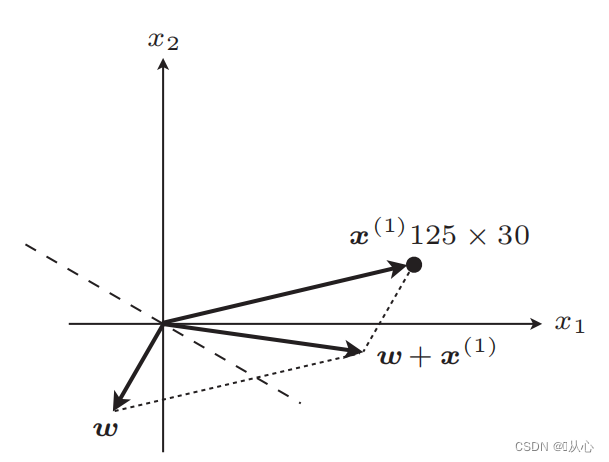
更新后直线

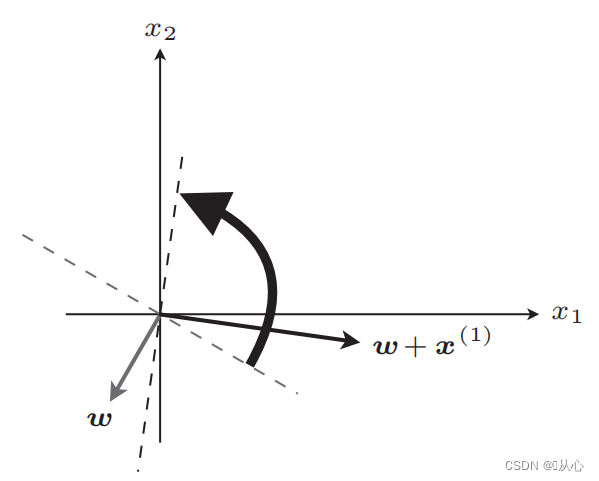
更新后，相等

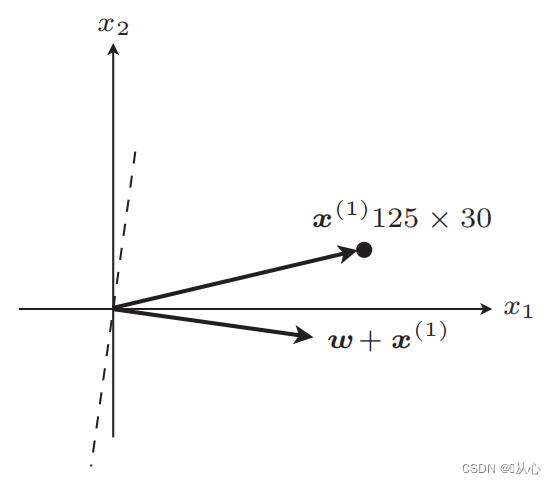
步骤：先随机确定一条直线（即随机确定一个权重向量w），内积代入一个真实值数据x，通过判别函数得到一个值（1或-1），若与原标签值相等，则权重向量不更新，若与原标签值不等，则用向量相加为权重向量更新。

！！！注意：感知机只能解决线性可分问题
线性可分：可以使用直线分类的情况
线性不可分：不能用直线分类

2、sigmoid函数

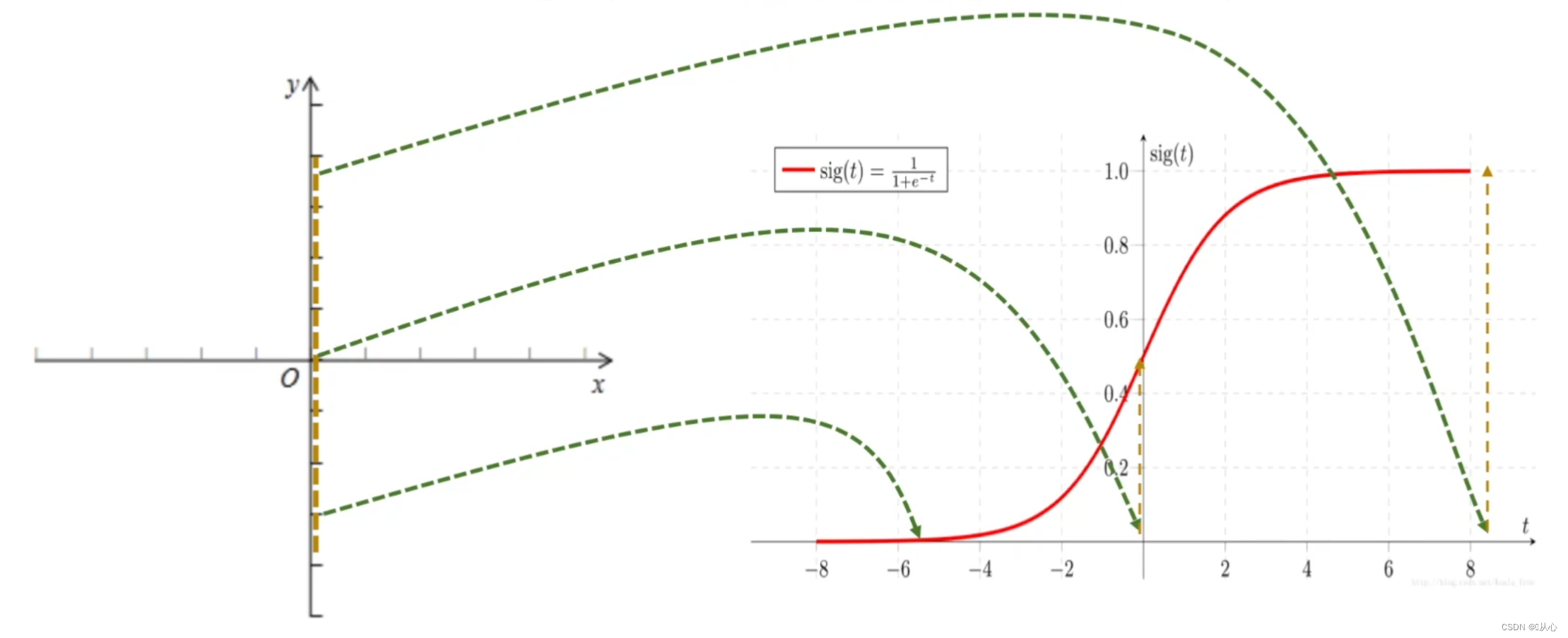
黑色为sigmoid函数，红色为阶跃函数（不连续）

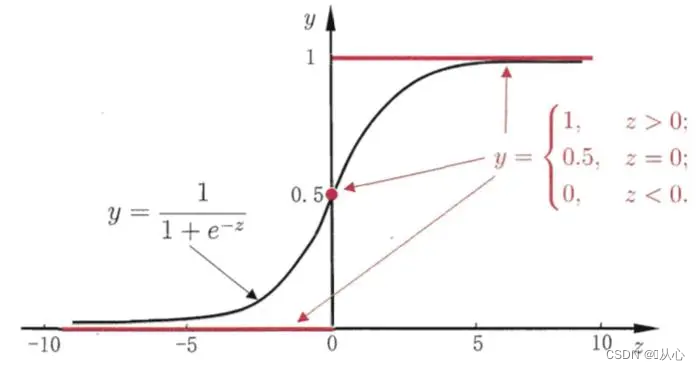
作用：逻辑回归的输入就是一个线性回归的结果，我们在线性回归中可以得到一个预测值，Sigmoid 函数将任意的输入映射到了[0,1]区间，这样就完成了由值到概率的转换，也就是分类任务。

3、逻辑回归

3.1、模型定义

逻辑回归=线性回归+sigmoid函数

线性回归：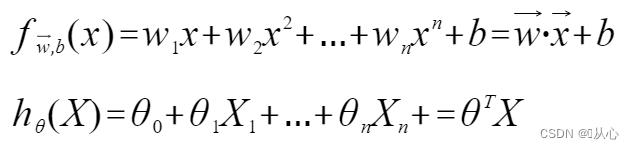

sigmoid函数：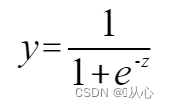

逻辑回归：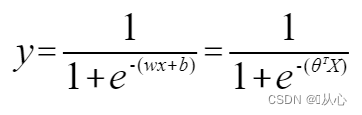

为了让y表示标签，改为：

做概率使用：

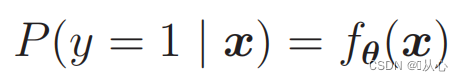
3.2、判别函数

即可以通过概率来区分类别

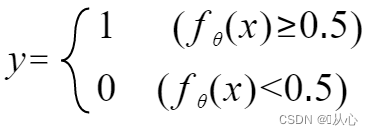
3.3、决策边界

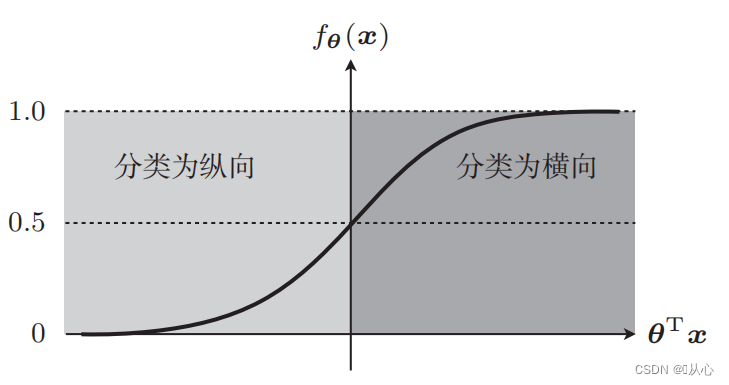
可以改写为如下形式：

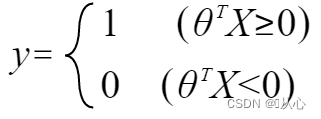
当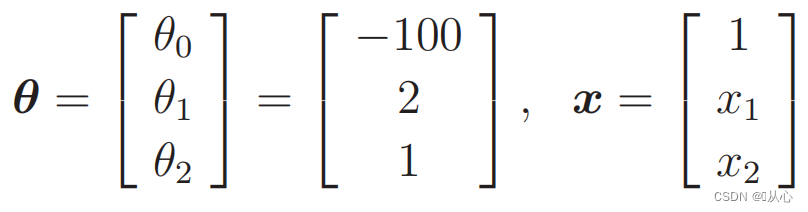

代入数据：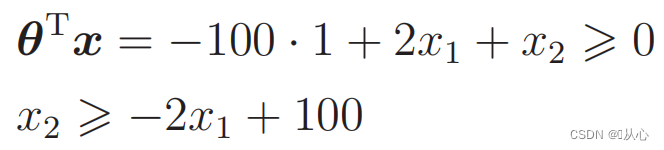

既有这样的图

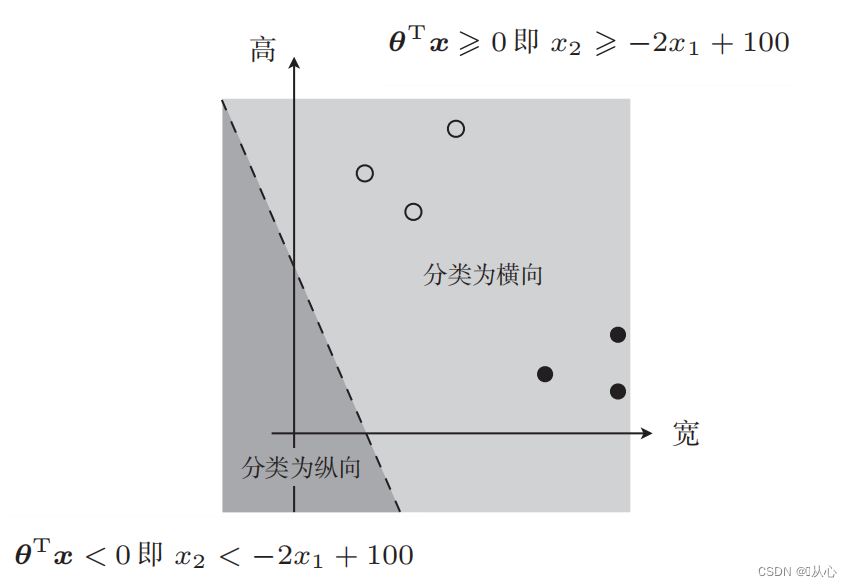这样用于数据分类的直线就是决策边界

3.4、目标函数（对数似然函数）

我们希望是这样的：
当y=1时，P(y=1|x)是最大的
当y=0时，P(y=0|x)是最大的

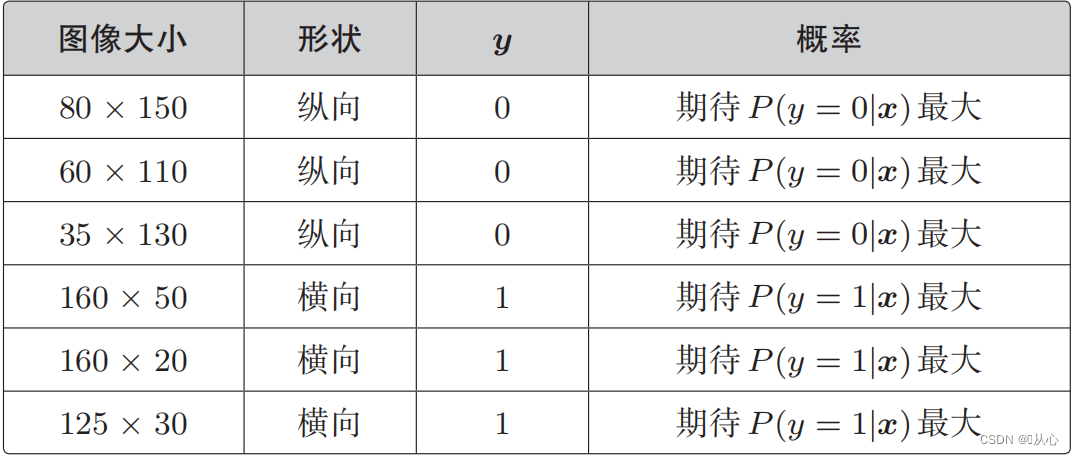
似然函数（联合概率）：这里是概率我们希望它最大化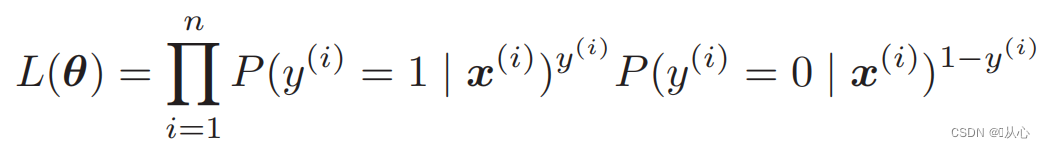

对数似然函数：直接对似然函数进行微分比较困难，需要先取对数

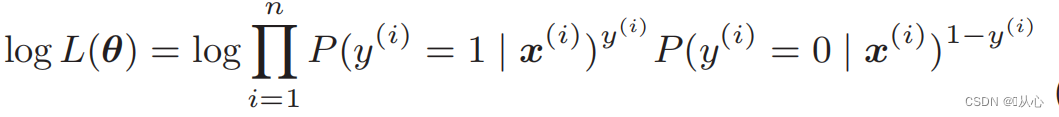
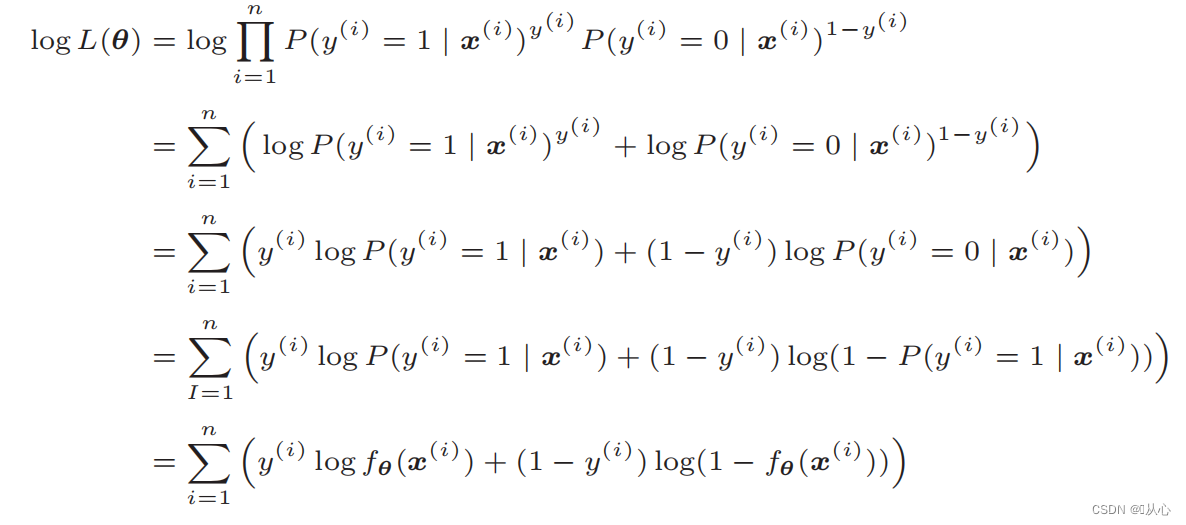
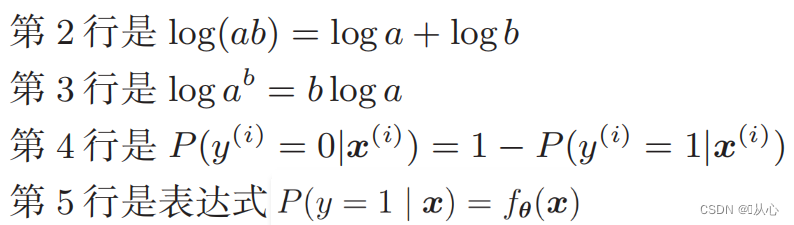
变形后即为：

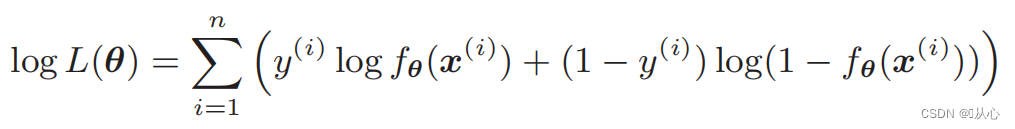
3.4、参数估计（梯度下降）

似然函数的微分：

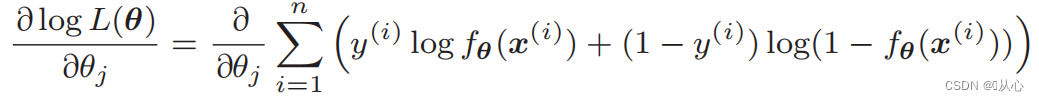
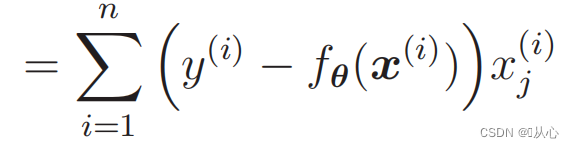
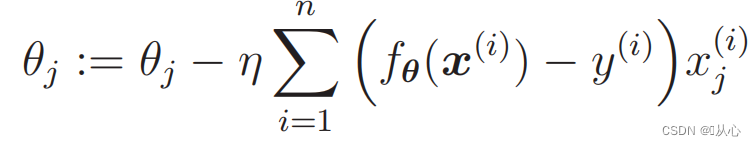
3、优缺点

3.1、优点：

1. 实现简单：逻辑回归是一种简单的算法，容易理解和实现。
2. 计算效率高：逻辑回归的计算量相对较小，适用于大规模数据集。
3. 可解释性强：逻辑回归输出结果是概率值，可以直观地解释模型的输出。

3.2、缺点：

1. 线性可分性要求：逻辑回归是一种线性模型，对于非线性可分的问题表现较差。
2. 特征相关性问题：逻辑回归对输入特征之间的相关性较为敏感，当特征之间存在较强相关性时，可能导致模型的性能下降。
3. 过拟合问题：当样本特征过多或样本数量较少时，逻辑回归容易出现过拟合的问题。

三、**算法实现

1、获取数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib notebook# 读取数据
train=pd.read_csv('csv/images2.csv')
train_x=train.iloc[:,0:2]
train_y=train.iloc[:,2]
# print(train_x)
# print(train_y)# 绘图
plt.figure()
plt.plot(train_x[train_y ==1].iloc[:,0],train_x[train_y ==1].iloc[:,1],'o')
plt.plot(train_x[train_y == 0].iloc[:,0],train_x[train_y == 0].iloc[:,1],'x')
plt.axis('scaled')
# plt.axis([0,500,0,500])
plt.show()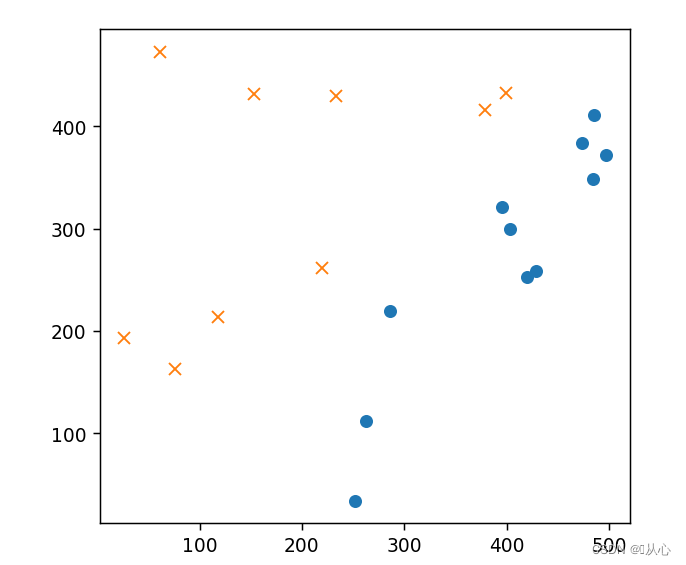

2、数据处理

# 初始化参数
theta=np.random.randn(3)# 标准化
mu = train_x.mean(axis=0)
sigma = train_x.std(axis=0)
# print(mu,sigma)def standardize(x):return (x - mu) / sigmatrain_z = standardize(train_x)
# print(train_z)# 增加 x0
def to_matrix(x):x0 = np.ones([x.shape[0], 1])return np.hstack([x0, x])X = to_matrix(train_z)# 绘图
plt.figure()
plt.plot(train_z[train_y ==1].iloc[:,0],train_z[train_y ==1].iloc[:,1],'o')
plt.plot(train_z[train_y == 0].iloc[:,0],train_z[train_y == 0].iloc[:,1],'x')
plt.axis('scaled')
# plt.axis([0,500,0,500])
plt.show()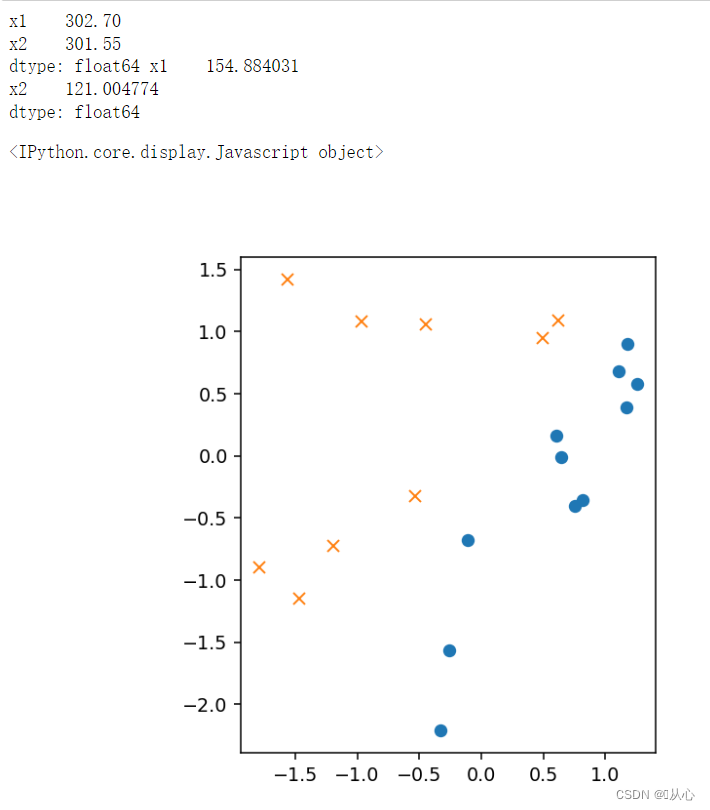

3.sigmoid函数和判别函数

# sigmoid 函数
def f(x):return 1 / (1 + np.exp(-np.dot(x, theta)))# 分类函数
def classify(x):return (f(x) >= 0.5).astype(np.int)

4.参数设置与训练

# 学习率
ETA = 1e-3# 重复次数
epoch = 5000# 更新次数
count = 0
print(f(X))# 重复学习
for _ in range(epoch):theta = theta - ETA * np.dot(f(X) - train_y, X)# 日志输出count += 1print('第 {} 次 : theta = {}'.format(count, theta))

5.绘图确认

# 绘图确认
plt.figure()
x0 = np.linspace(-2, 2, 100)
plt.plot(train_z[train_y ==1].iloc[:,0],train_z[train_y ==1].iloc[:,1],'o')
plt.plot(train_z[train_y == 0].iloc[:,0],train_z[train_y == 0].iloc[:,1],'x')
plt.plot(x0, -(theta[0] + theta[1] * x0) / theta[2], linestyle='dashed')
plt.show()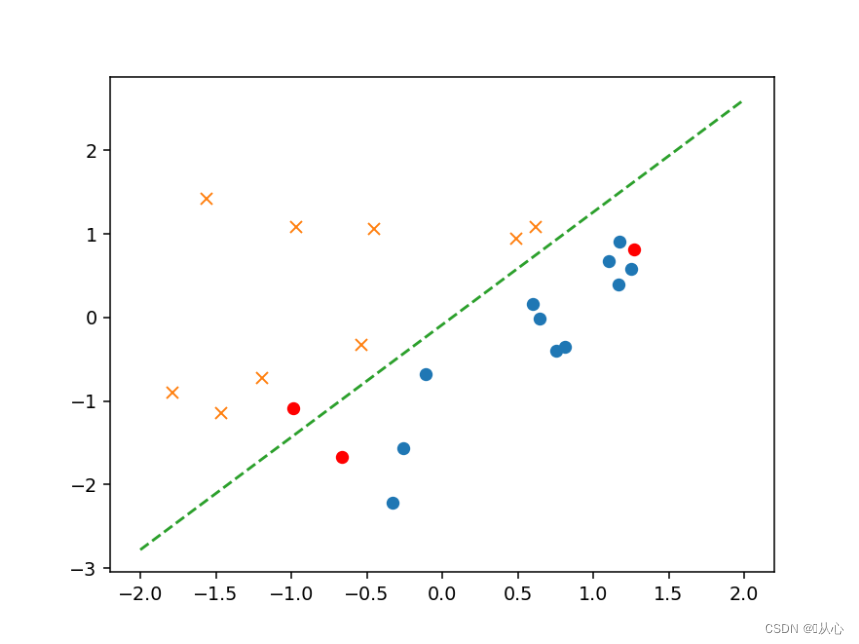

6.验证

# 验证
text=[[200,100],[500,400],[150,170]]
tt=pd.DataFrame(text,columns=['x1','x2'])
# text=pd.DataFrame({'x1':[200,400,150],'x2':[100,50,170]})
x=to_matrix(standardize(tt))
print(x)
a=f(x)
print(a)b=classify(x)
print(b)plt.plot(x[:,1],x[:,2],'ro')

四、接口实现

1、乳腺癌数据集介绍

1.1、API

from sklearn.datasets import load_breast_cancer

1.2、基本信息

# 键
print("乳腺癌数据集的键：",breast_cancer.keys())# 特征值名字、目标值名字
print("乳腺癌数据集的特征数据形状：",breast_cancer.data.shape)
print("乳腺癌数据集的目标数据形状：",breast_cancer.target.shape)print("乳腺癌数据集的特征值名字：",breast_cancer.feature_names)
print("乳腺癌数据集的目标值名字：",breast_cancer.target_names)# print("乳腺癌数据集的特征值：",breast_cancer.data)
# print("乳腺癌数据集的目标值：",breast_cancer.target)# 返回值
# print("乳腺癌数据集的返回值：\n", breast_cancer)
# 返回值类型是bunch--是一个字典类型# 描述
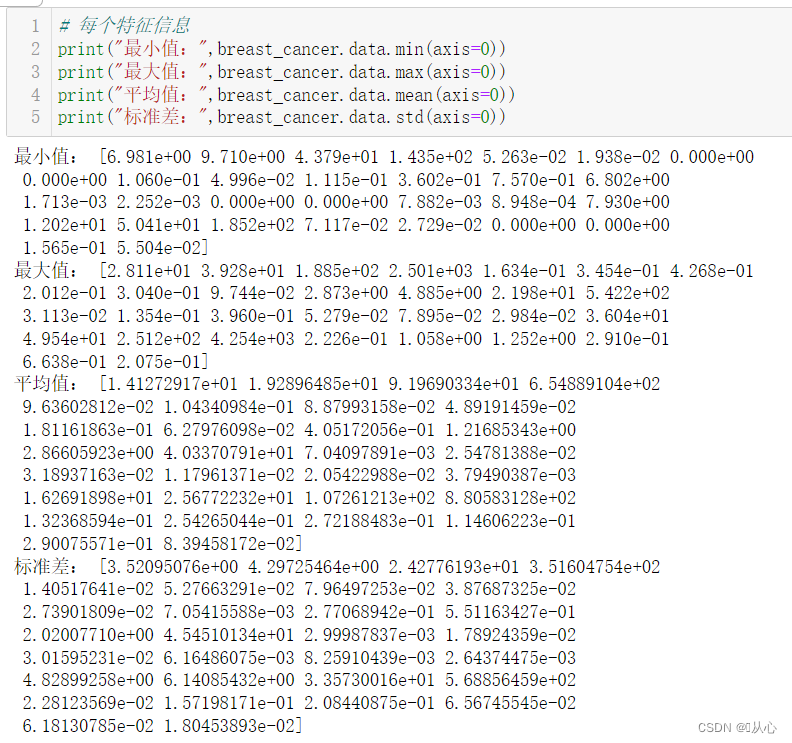
# print("乳腺癌数据集的描述：",breast_cancer.DESCR)# 每个特征信息
print("最小值：",breast_cancer.data.min(axis=0))
print("最大值：",breast_cancer.data.max(axis=0))
print("平均值：",breast_cancer.data.mean(axis=0))
print("标准差：",breast_cancer.data.std(axis=0))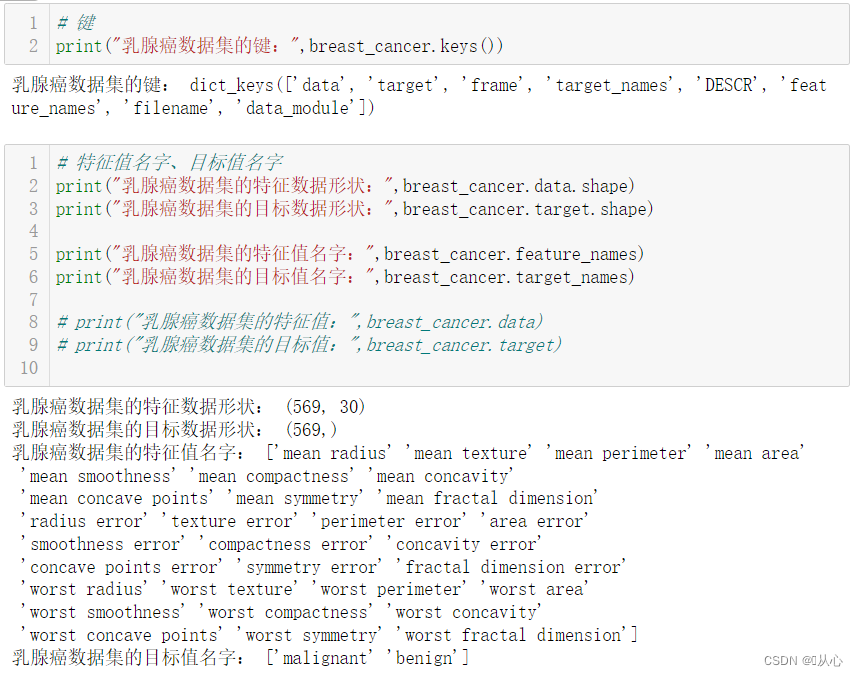

# 取其中间两列特征
x=breast_cancer.data[0:569,0:2]
y=breast_cancer.target[0:569]samples_0 = x[y==0, :]
samples_1 = x[y==1, :]# 实现可视化
plt.figure()
plt.scatter(samples_0[:,0],samples_0[:,1],marker='o',color='r')
plt.scatter(samples_1[:,0],samples_1[:,1],marker='x',color='y')
plt.xlabel('mean radius')
plt.ylabel('mean texture')
plt.show()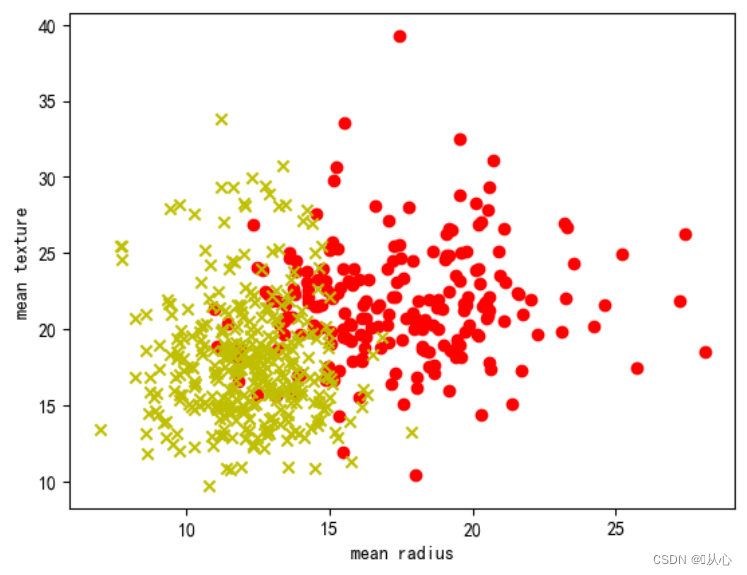

# 绘制每个特征直方图，显示特征值的分布情况。
for i, feature_name in enumerate(breast_cancer.feature_names):plt.figure(figsize=(6, 4))sns.histplot(breast_cancer.data[:, i], kde=True)plt.xlabel(feature_name)plt.ylabel("数量")plt.title("{}直方图".format(feature_name))plt.show()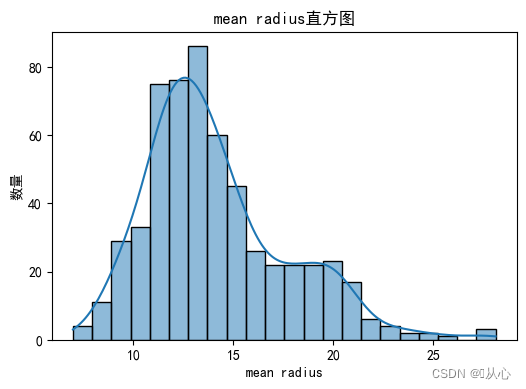

# 绘制箱线图，展示每个特征最小值、第一四分位数、中位数、第三四分位数和最大值概括。
plt.figure(figsize=(10, 6))
sns.boxplot(data=breast_cancer.data, orient="v")
plt.xticks(range(len(breast_cancer.feature_names)), breast_cancer.feature_names, rotation=90)
plt.xlabel("特征")
plt.ylabel("值")
plt.title("特征箱线图")
plt.show()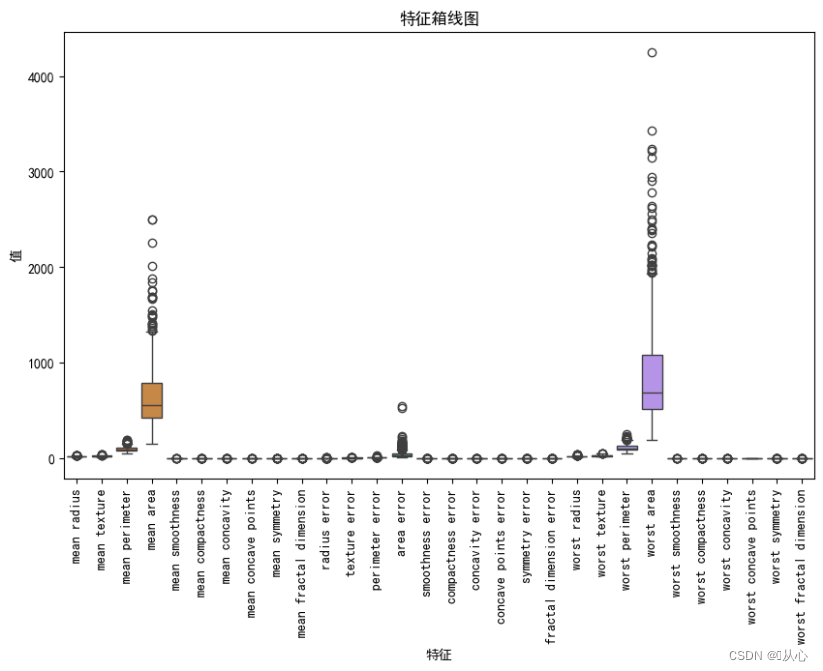

1.3、缺失值与异常值

# 创建DataFrame对象
df = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)# 检测缺失值
print("缺失值数量：")
print(df.isnull().sum())# 检测异常值
print("异常值统计信息：")
print(df.describe())
# 使用.describe()方法获取数据集的统计信息，包括计数、均值、标准差、最小值、25%分位数、中位数、75%分位数和最大值。

1.4、相关性

# 创建DataFrame对象
df = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)# 计算相关系数
correlation_matrix = df.corr()# 可视化相关系数热力图
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm")
plt.title("Correlation Heatmap")
plt.show()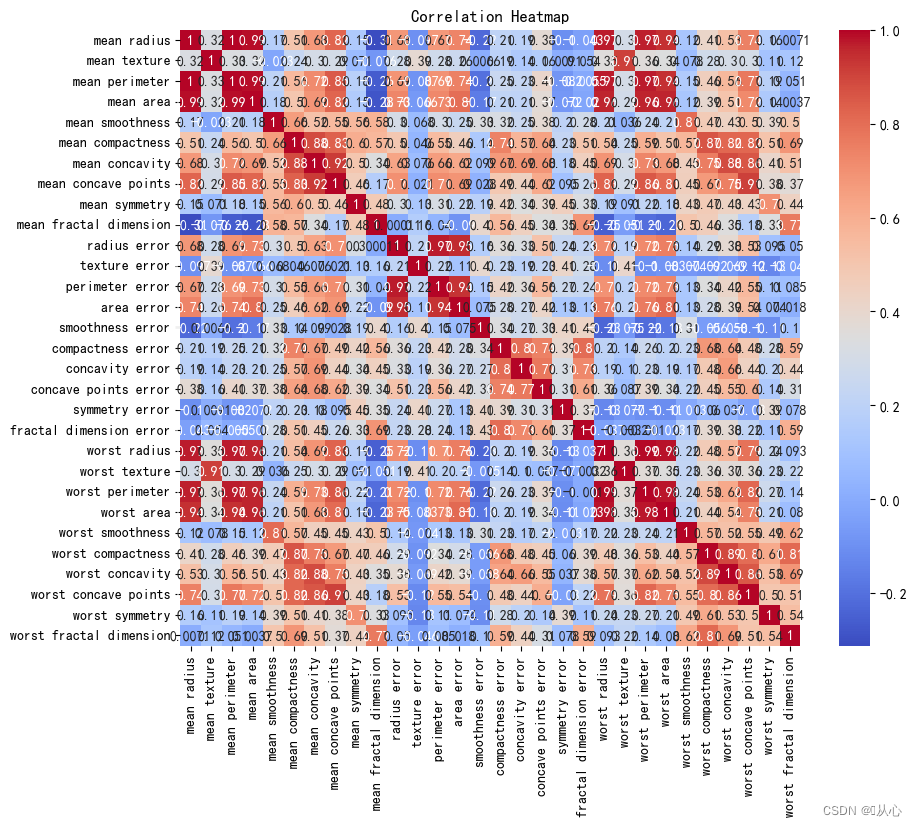

2、API

sklearn.linear_model.LogisticRegression导入：
from sklearn.linear_model import LogisticRegression语法：
LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)solver可选参数:{'liblinear', 'sag', 'saga','newton-cg', 'lbfgs'}，默认: 'liblinear'；用于优化问题的算法。对于小数据集来说，“liblinear”是个不错的选择，而“sag”和'saga'对于大型数据集会更快。对于多类问题，只有'newton-cg'， 'sag'， 'saga'和'lbfgs'可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。penalty：正则化的种类C：正则化力度

2、流程

2.1、获取数据

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegression# 获取数据
breast_cancer = load_breast_cancer()

2.2、数据预处理

# 划分数据集
x_train,x_test,y_train,y_test = train_test_split(breast_cancer.data, breast_cancer.target, test_size=0.2, random_state=1473)

2.3、特征工程

2.4、模型训练

# 实例化学习器
lr = LogisticRegression(max_iter=10000)# 模型训练
lr.fit(x_train, y_train)print("建立的逻辑回归模型为：\n", lr)

2.5、模型评估

# 用模型计算测试值，得到预测值
y_pred = lr.predict(x_test)
print('预测前20个结果为：\n', y_pred[:20])# 求出预测结果的准确率和混淆矩阵
from sklearn.metrics import accuracy_score, confusion_matrix,precision_score,recall_score
print("预测结果准确率为：", accuracy_score(y_test, y_pred))
print("预测结果混淆矩阵为：\n", confusion_matrix(y_test, y_pred))print("预测结果查准率为：", precision_score(y_test, y_pred))
print("预测结果召回率为：", recall_score(y_test, y_pred))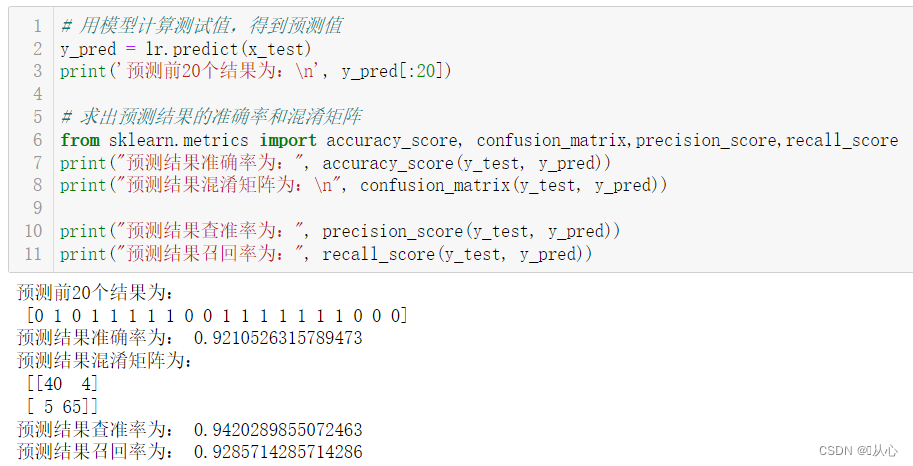

from sklearn.metrics import roc_curve,roc_auc_score,aucfpr,tpr,thresholds=roc_curve(y_test,y_pred)plt.plot(fpr, tpr)
plt.axis("square")
plt.xlabel("假正例率/False positive rate")
plt.ylabel("正正例率/True positive rate")
plt.title("ROC curve")
plt.show()print("AUC指标为：",roc_auc_score(y_test,y_pred))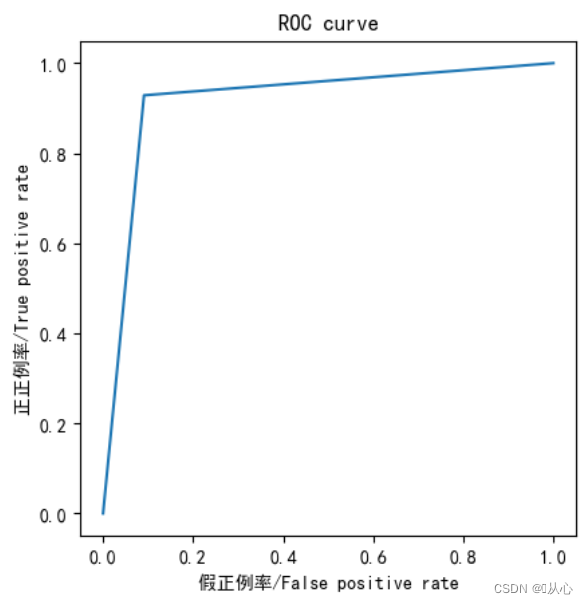

# 求出预测取值和真实取值一致的数目 
num_accu = np.sum(y_test == y_pred)
print('预测对的结果数目为：', num_accu)
print('预测错的结果数目为：', y_test.shape[0]-num_accu)
print('预测结果准确率为：', num_accu/y_test.shape[0])