第八章 贪心算法 part02
贪心 局部最优解推出全局最优 ,而且想不到反例,那么就试一试贪心
将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解
只要想清楚 局部最优 是什么,如果推导出全局最优,其实就够了。
贪心没有套路,说白了就是常识性推导加上举反例。
122.买卖股票的最佳时机II
本题解法很巧妙,**本题大家可以先自己思考一下然后再看题解,会有惊喜! **
https://programmercarl.com/0122.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BAII.html
55. 跳跃游戏
本题如果没接触过,很难想到,所以不要自己憋时间太久,读题思考一会,没思路立刻看题解
https://programmercarl.com/0055.%E8%B7%B3%E8%B7%83%E6%B8%B8%E6%88%8F.html
45.跳跃游戏II
本题同样不容易想出来。贪心就是这样,有的时候 会感觉简单到离谱,有时候,难的不行,主要是不容易想到。
https://programmercarl.com/0045.%E8%B7%B3%E8%B7%83%E6%B8%B8%E6%88%8FII.html
1005.K次取反后最大化的数组和
本题简单一些,估计大家不用想着贪心 ,用自己直觉也会有思路。
https://programmercarl.com/1005.K%E6%AC%A1%E5%8F%96%E5%8F%8D%E5%90%8E%E6%9C%80%E5%A4%A7%E5%8C%96%E7%9A%84%E6%95%B0%E7%BB%84%E5%92%8C.html
122.买卖股票的最佳时机II
题目链接
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/description/
解题思路
如果想到其实最终利润是可以分解的,那么本题就很容易了!
如何分解呢?
假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。
相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
此时就是把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑!
只收集正利润就是贪心所贪的地方
局部最优:收集每天的正利润,全局最优:求得最大利润。
局部最优可以推出全局最优,找不出反例,试一试贪心!
code
class Solution {public int maxProfit(int[] prices) {if(prices==null || prices.length<1){return 0;}int result=0;//i=1 至少第二天才会有利润for(int i=1;i<prices.length;i++){if(prices[i]>prices[i-1]){result+=prices[i]-prices[i-1];}}return result;}
}
55. 跳跃游戏
题目链接
https://leetcode.cn/problems/jump-game/description/
解题思路
只能是接触各种类型的题目锻炼自己的贪心思维!
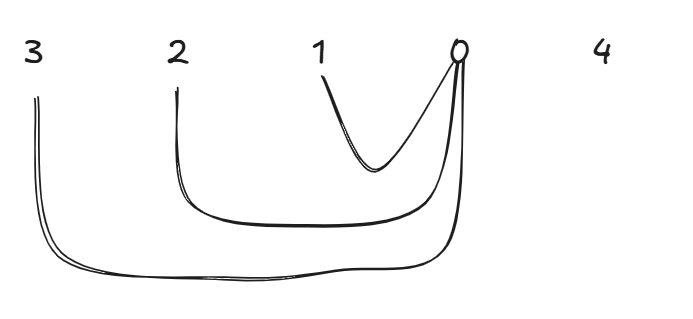
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
局部最优推出全局最优,找不出反例,试试贪心!而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。
如果 cover 大于等于了终点下标,直接 return true 就可以了。
code
class Solution {//贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。public boolean canJump(int[] nums) {int cover=0;for(int i=0;i<=cover;i++){cover=Math.max(i+nums[i],cover);//计算当前i位置的覆盖范围,去前一个和当前的最大覆盖范围。if(cover>=nums.length-1){//可覆盖的范围大于数组最后一个下标return true;}}return false;}
}
return false
return true
45.跳跃游戏II
题目链接
https://leetcode.cn/problems/jump-game-ii/description/
解题思路
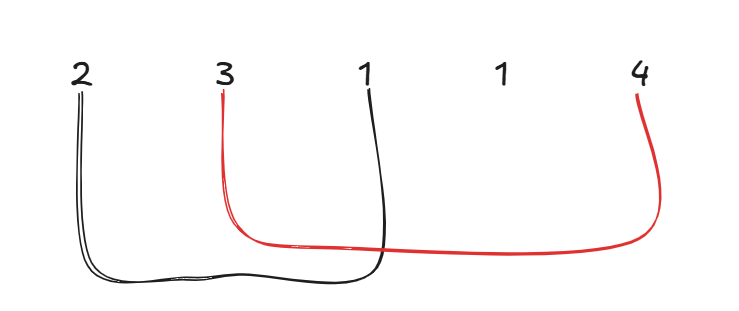
贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最少步数。
所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最少步数!
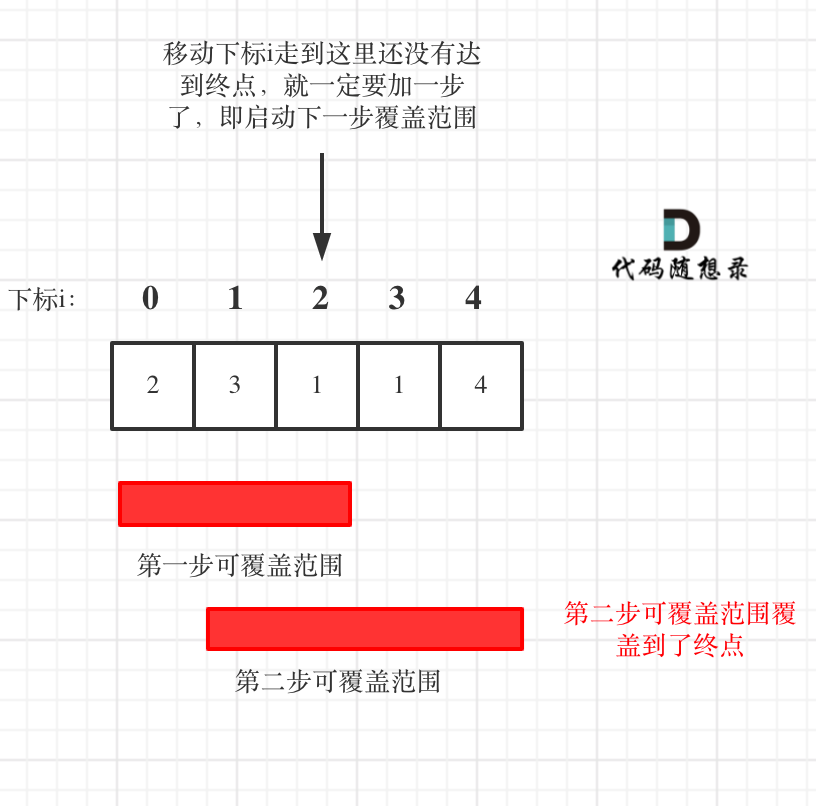
这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖。
如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
code
class Solution {public int jump(int[] nums) {//特殊处理,只有一个元素,只需要走0步,return 0if(nums.length==1){return 0;}int curDistance=0;int nextDistance=0;int ans=0;for(int i=0;i<nums.length;i++){//nextDistance 记录最大覆盖范围nextDistance=Math.max(nums[i]+i,nextDistance);//当i=0时候记录第一步 然后当i遍历到第一步走完时,计算下是否符合,以此类推if(i==curDistance){ans++;curDistance=nextDistance;//预备下一步,nextDistance 是在 curDistance遍历过程中记录可走的最大距离if(curDistance>=nums.length-1) break;}}return ans;}
}
图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!
1005.K次取反后最大化的数组和
题目链接
https://leetcode.cn/problems/maximize-sum-of-array-after-k-negations/description/
解题思路
贪心的思路,局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。
那么如果将负数都转变为正数了,K依然大于0,此时的问题是一个有序正整数序列,如何转变K次正负,让 数组和 达到最大。
那么又是一个贪心:局部最优:只找数值最小的正整数进行反转,当前数值和可以达到最大,全局最优:整个 数组和 达到最大第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
第二步:从前向后遍历,遇到负数将其变为正数,同时K–
第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
第四步:求和
code
class Solution {public int largestSumAfterKNegations(int[] nums, int k) {//1.排序按绝对值从大到小排序nums= Arrays.stream(nums).boxed().sorted((o1, o2) -> Math.abs(o2) - Math.abs(o1)).mapToInt(a -> a).toArray();for(int i=0;i<nums.length;i++){//k大于0 反转负数if(nums[i]<0&&k>0){nums[i]=-nums[i];k--;}}//如果k依然大于0,此时数组都是正数了,反转最后一个最小的元素即可//k是偶数不用反转,奇数反转if(k%2==1) nums[nums.length-1]=-nums[nums.length-1];return Arrays.stream(nums).sum();}
}


















