翻译: 可视化深度学习反向传播原理一

在这里插入图片描述
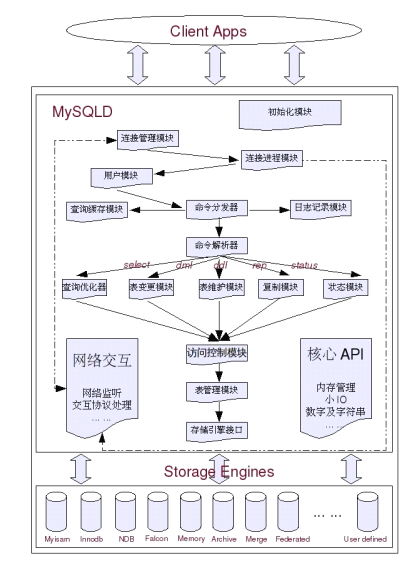
本期我们来讲反向传播也就是神经网络学习的核心算法稍微回顾一下我们之前讲到哪里之后

首先我要撇开公式不提直观地过一遍这个算法到底在做什么
在这里插入图片描述

然后如果你们有人想认真看里头的数学下一期影片我会解释这一切背后的微积分如果你看了前两期影片或者你已经有足够背景知识直接空降来这一期影片的话你一定知道神经网络是什么以及它如何前馈信息的
在这里插入图片描述

这里我们考虑的经典例子就是手写数字识别数字的像素值被输入到网络第一层的784个神经元里
这里我展示的是有2层16个神经元隐含层 10个神经元的输出层代表网络最终给出的选择
在这里插入图片描述

我也假设你们已经理解了上期说到的梯度下降法理解了所谓学习就是指我们要找到特定的权重偏置从而使一个代价函数最小化
在这里插入图片描述

稍许提醒一下计算一个训练样本的代价你需要求出网络的输出与期待的输出之间每一项的差的平方和
在这里插入图片描述

然后对于成千上万个训练样本都这么算一遍最后取平均这就得到了整个网络的代价值
在这里插入图片描述

如果你嫌这还不够复杂的话上集内容也讲到了
我们要求的是代价函数的负梯度
在这里插入图片描述

它告诉你如何改变所有连线上的权重偏置才好让代价下降得最快
在这里插入图片描述

反向传播算法正是用来求这个复杂到爆的梯度的

在这里插入图片描述

我希望大家能够把上集中提到的一点牢牢记住毕竟13000维的梯度向量说它是难以想象都不为过
在这里插入图片描述

所以这里大家请记住另一套思路梯度向量每一项的大小是在告诉大家代价函数对于每个参数有多敏感比如说你走了一段我讲的过程计算了负梯度对应这条线上这个权重的一项等于3.2，而对应这条边上的一项等于0.1
在这里插入图片描述

你可以这么来理解第一个权重对代价函数的值有32倍的影响力如果你稍微改变一下第一个权重它对代价值造成的变化
在这里插入图片描述

就是改变第二个权重同等大小下的32倍
在这里插入图片描述

就我个人而言我刚开始学习反向传播的时候我觉得最容易搞混的部分就是各种符号和上标下标不过一旦你厘清了算法的思路算法的每一步其实都挺直观的其实就是把许许多多微小的调整一层进一层地进行下去而已所以开始讲解时我将完全抛弃所有的符号
在这里插入图片描述

给大家一步步解释每一个训练样本会对权重偏置的调整造成怎样的影响因为代价函数牵扯到对成千上万个训练样本的代价取平均值
在这里插入图片描述

所以我们调整每一步梯度下降用的权重偏置也会基于所有的训练样本原理上是这么说
在这里插入图片描述

但为了计算效率之后咱们会讨个巧从而不必每一步都非得要计算所有的训练样本
在这里插入图片描述

还需要说明一点我们现在只关注一个训练样本就这张2 这一个训练样本会对调整权重和偏置造成怎样的影响呢？
在这里插入图片描述

现在假设网络还没有完全训练好那么输出层的激活值看起来就很随机也许就会出现0.5、0.8、0.2 等等等等
在这里插入图片描述

我们并不能直接改动这些激活值只能改变权重和偏置值
在这里插入图片描述

但记住我们想要输出层出现怎样的变动还是很有用的
在这里插入图片描述

因为我们希望图像最终的分类结果是2 我们希望第三个输出值变大其他数值变小并且变动的大小应该与现在值和目标值之间的差呈正比并且变动的大小应该与现在值和目标值之间的差呈正比
在这里插入图片描述

举个例子增加数字“2”神经元的激活值
就应该比减少数字“8”神经元的激活值来得重要因为后者已经很接近它的目标了
在这里插入图片描述

那好我们更进一步就来关注下这一个神经元我们要让这里面的激活值变大还记得这个激活值是把前一层所有激活值的加权和加上一个偏置再通过sigmoid ReLU之类的挤压函数最后算出来的吧所以要增加这个激活值我们有三条大路可走一增加偏置二增加权重或者三改变上一层的激活值先来看如何调整权重各个权重它们的影响力各不相同
在这里插入图片描述