目录

1.树的知识总览

2.树的基本概念

        i.部分名词

        ii.结点间的关系

        iii.属性

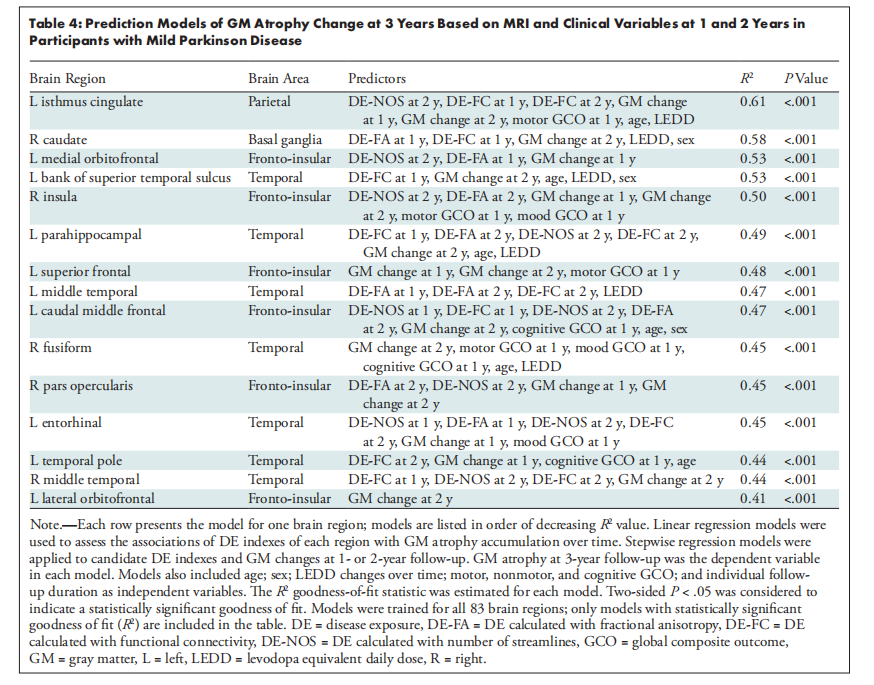
3.树的常考性质

        i.结点数

        ii.度为m的树 与 m叉树 的区别（m>0）

        iii.树的第 i 层的结点数（i>=1）  ​编辑

        iiii. 高度为h的m叉树的结点数

        iiiii.高度为h、度为m的树的结点数

        iiiiii.具有n个结点的m叉树的最小高度

---

1.树的知识总览

2.树的基本概念

        i.部分名词

        空树：结点数为0的树。

        非空树：

        · 有且仅有一个根节点的树。

        · 没有后继的结点称为“叶子结点”。

        · 有后继的称为“分支结点”。

        · 没有前驱的结点称为“根结点”，且除根节点外，每个结点有且仅有一个前驱。

        子树：当n>1（n为树的结点数目）时，根节点外的其余结点可分为m个互不相交的集合，其中的每个集合本身又是一棵树，称为根节点的子树。

        有序树：在逻辑上，树中结点的各子树，从左到右是有次序的，不可以改变位置，如下文的家谱图。

        无序树：各子树，从左到右无次序，位置可以随意互换。

        森林：由m棵互不相交的树组成的集合。

        

        ii.结点间的关系

        · 祖先结点： 从“你”（某个非根结点）到“爷爷”（根节点），路径上经过的所有结点（包括根节点）都是“你”的祖先结点。

        · 子孙结点：一个节点向下延申出一切（直接后继、间接后继）都是他的子孙节点，如“爷爷”向下延申到最低端的所有结点都是“爷爷”的“子孙”，如“你”的“子孙”就是K，L。

        · 父节点：显而易见。

        · 孩子结点：“你”就是“父亲”的孩子结点。

        · 兄弟结点：F 就是“你”的兄弟结点。

        · 堂兄弟结点：G 就是“你”的堂兄弟结点。

        · 结点之间的路径：只能从上往下，即树里的边其实是有方向的，方向由根节点的方向沿边指向叶子结点。

        · 路径长度：经过了几条边。（路径上，边的数目）

        iii.属性

        结点的层次（深度）：从上往下数，根节点是第一层。

        结点的高度：从下往上数，各分支的叶子结点不一定在同一高度（也不一定在同一层）。

        树的高度（深度）：总共的层数（最高高度）。

        结点的度：有几个孩子（有几个分支，如上文的爷爷有三个孩子，即三度）。

        树的度：各结点中的最大度。

3.树的常考性质

        i.结点数

        结点数 = 总度数 + 1

        ii.度为m的树 与 m叉树 的区别（m>0）

        度为m的树：其中的结点的度数最多为m，至少且必须有一个结点度数为m。此树不可为空。

        m叉树：其中的结点的度数最多为m，各节点的度数可以没有达到m的。所以，此树可以为空。

        iii.树的第 i 层的结点数（i>=1）  

        iiii. 高度为h的m叉树的结点数

        注：至少有h个结点，每一个高度都只有一个结点。 

        iiiii.高度为h、度为m的树的结点数

        至少有 h+m-1 个结点

        iiiiii.具有n个结点的m叉树的最小高度