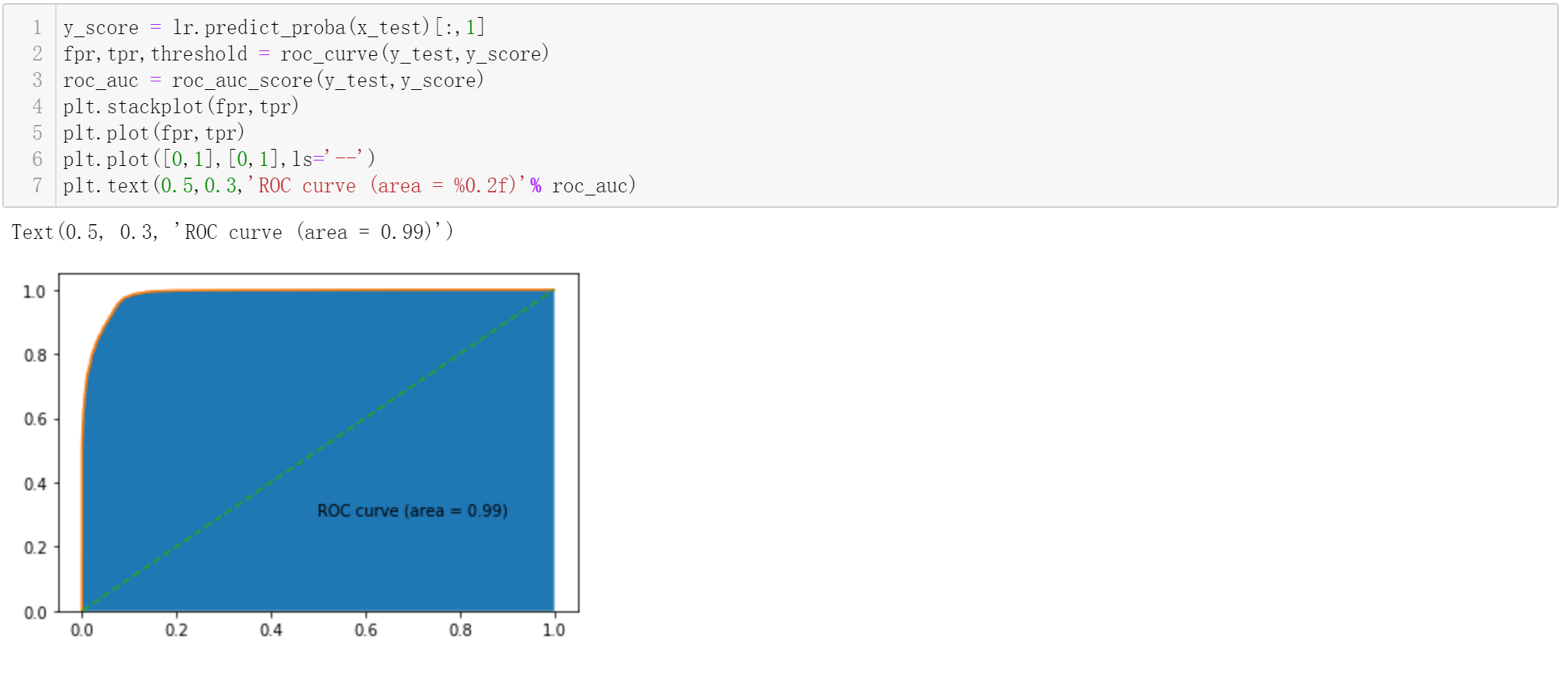
信息量

以前我也一直只是知道信息量的计算公式，也有想过为什么会是这样，但是因为要学的东西太多了，就没怎么深究，直到看了“交叉熵”如何做损失函数？打包理解“信息量”、“比特”、“熵”、“KL散度”、“交叉熵”王木头的视频，才有了比较值观且深刻的理解了。

接下来看这么一幅图：

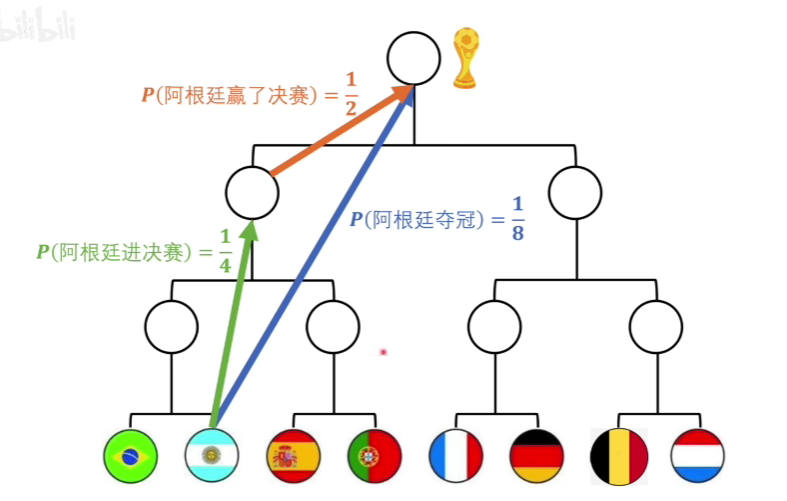
如何衡量信息量呢

我们看图可以发现，阿根廷进入决赛+阿根廷赢了决赛 = 阿根廷夺冠
这二者再说一件事情，理应信息量一样大，这应该比较好理解。

那么我们就能够推出信息量的定义了

因为需要满足上面的式子，我们容易看出，式子里得带着log

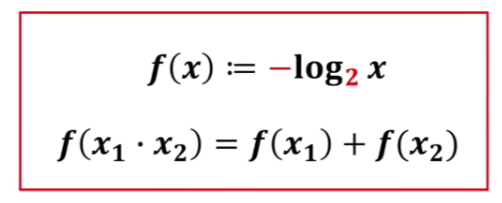
这里以2为底，可以用比特来作为计算出的信息量的单位。
这里取个-因为概率都是<1的，计算出来的都是负数，因为原来概率小的事情发生了，给我们直观的感受应该是信息量越大，因此取个-来迎合我们的感受。

信息量衡量的是一个事件从原来的不确定到确定，他的难度有多大，信息量越大，说明难度就越高。

熵

前面说到信息量是衡量一个事件从不确定到确定的花费，那么熵就是高一级，衡量一个系统从不确定到确定的花费，就称之为熵了。
下面再看这么一幅图：

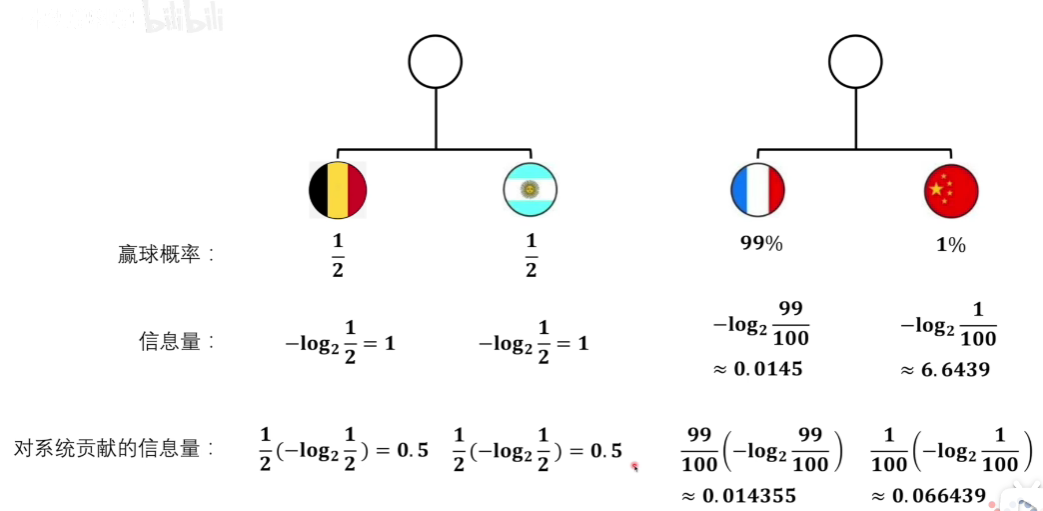
左右两边分别看成一个系统。
我们可以发现左边系统的熵=1
右边系统的熵=0.08左右
这说明左边系统从不确定到确定的难度远高于右边的系统。
这样符合我们直观的感受，两个势均力敌的人区分胜负，在没看到结局之前，谁也不敢妄下定论，说明从不确定到确定的难度会很大。

那么规范一下，我们系统熵的定义可以写成如下形式：

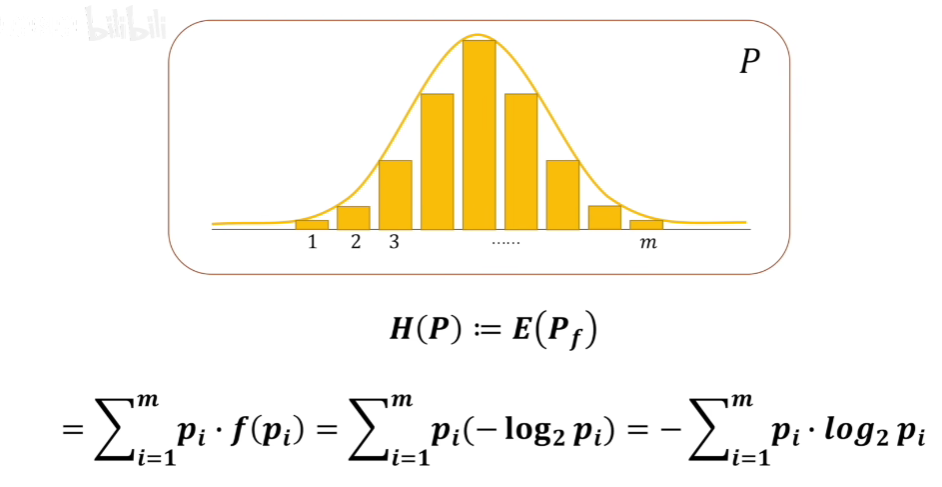
这样我们便得到了信息熵的定义，数学建模里客观评价中的熵权法中的信息熵的方式就是基于此，因为是根据数据中信息确定性程度（信息量包含的大小）来衡量权重。

KL散度（相对熵）

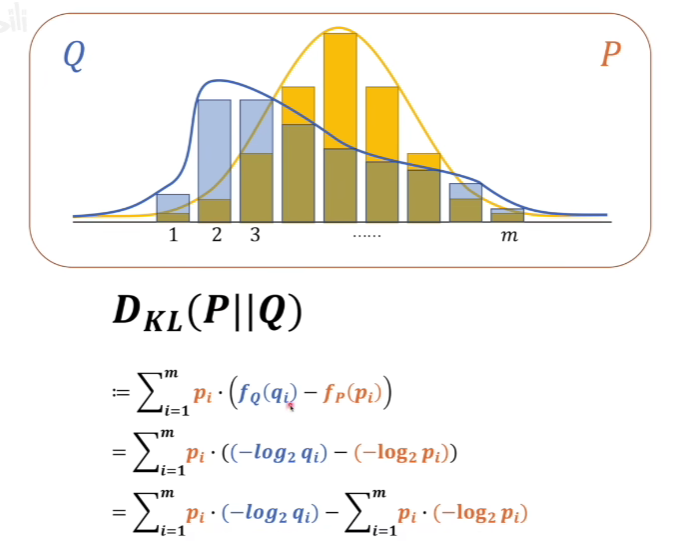
其中

分别代表两个概率系统的信息量。

这里的KL散度式子是以P为基准去考虑Q变成P的分布相差有多少信息量。

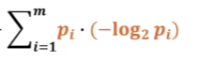
这一部分很容易看出，是P系统的信息熵。

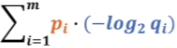
这一部分就是交叉熵了，可以用H(P，Q)来表达。

当KL散度=0时，说明两个概率分布情况时一样的。

根据：

可以说明，这里KL散度一定是大于等于0的

因此，如果我希望Q和P越接近，就是需要寻找交叉熵的最小值就行了，因为后面的式子是恒定的（因为以P为基准了，可以认为P相当于真实值，那么我需要的就是调整Q去接近P）。

对于连续性随机变量也可以定义KL散度：

交叉熵

通过KL散度的推导，我们发现，当以P为基准的时候，计算Q拟合P分布的差距其实就是考虑交叉熵最小即可。
那么放到神经网络中，当P为真实样本标签，Q为预测值的时候，我们就可以通过交叉熵来计算损失，从而进行反向传播，训练模型，从而使得预测值的Q与P的分布越来越近，从而达到比较好的一个效果。

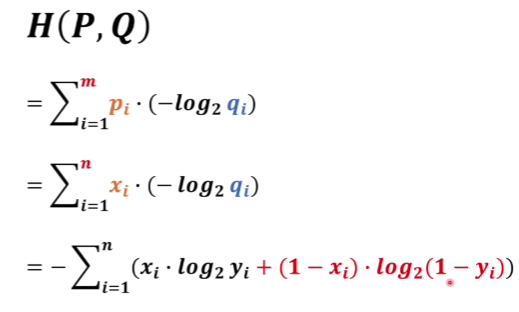
将KL散度推出交叉熵进行展开，我们可以发现就比较熟悉了。
假设x_i表示预测值，y_i表示预测值x_i正确的概率
那么1-x_i表示预测出来不是x_i，1-y_i表示预测出来不是x_i的概率

这也就是我们分类问题中经常使用的交叉熵损失函数了。

参考

KL散度超详细讲解
“交叉熵”如何做损失函数？打包理解“信息量”、“比特”、“熵”、“KL散度”、“交叉熵”