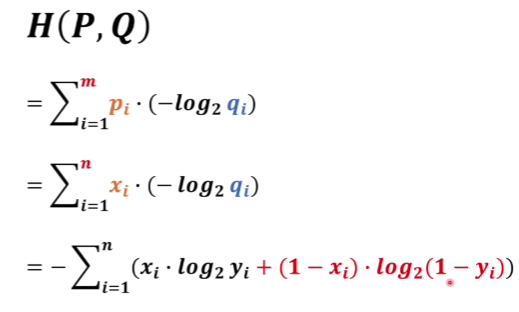2019-07-13
https://blog.csdn.net/landstream/article/details/82383503
https://blog.csdn.net/pipisorry/article/details/51695283
https://www.zhihu.com/question/41252833
https://cloud.tencent.com/developer/article/1397504
按顺序查看更容易理解
0、背景
在信息论中,熵是接收的每条消息中包含的信息的平均量,又被称为信息熵、信源熵、平均自信息量。这里, 消息代表来自分布或数据流中的事件、样本或特征。在信息世界,熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。
和热力学熵的联系:在1948年,克劳德·艾尔伍德·香农将热力学的熵,引入到信息论,因此它又被称为香农熵。物理学家和化学家对一个系统自发地从初始状态向前演进过程中,遵循热力学第二定律而发生的熵的变化更感兴趣。在传统热力学中,熵被定义为对系统的宏观测定,并没有涉及概率分布,而概率分布是信息熵的核心定义。
1、自信息
我们定义一个事件x = x 的自信息(self-information): I(x)=−logP(x)
自信息只处理单个的输出。
2、香农熵(对于离散变量)
我们可以用香农熵(Shannon entropy)来对整个概率分布中的不确定性总量进行量化:
H(x)=EX−P[I(x)]=−EX−P[logP(x)]
信息熵公式的来源
信息:信息量可以被看成在学习 x 的值的时候的“惊讶程度”。如果有人告诉我们一个相当不可能的事件发生了,我们收到的信息要多于我们被告知某个很可能发生的事件发生时收到的信息,如果我们知道某件事情一定会发生,那么我们就不会接收到信息。于是,我们对于信息内容的度量将依赖于概率分布 p(x) ,因此我们想要寻找一个函数 h(x) ,它是概率 p(x) 的单调递减函数,表达了信息的内容。 h(·) 的形式可以这样寻找:如果我们有两个不相关的事件 x 和 y ,那么我们观察到两个事件同时发生时获得的信息应该等于观察到事件各自发生时获得的信息之和,即 h(x, y) = h(x) + h(y) {采用概率分布的对数作为信息的量度的原因是其可加性。例如,投掷一次硬币提供了1 Sh的信息,而掷 m 次就为 m 位。更一般地,你需要用 log2(n) 位来表示一个可以取 n 个值的变量。}。两个不相关事件是统计独立的,因此 p(x, y) = p(x)p(y) 。根据这两个关系,很容易看出 h(x) 一定与 p(x) 的对数有关,满足这两个条件的函数肯定是负对数形式。因此,我们有
h(x) = − log 2 p(x)
负号确保了信息一定是正数或者是零。注意,低概率事件 x 对应于高的信息量。
假设一个发送者想传输一个随机变量的值给接收者。这个过程中,他们传输的平均信息量通可以通过求上式关于概率分布 p(x) 的期望得到。即事件的概率分布和每个事件的信息量构成了一个随机变量,这个随机变量的均值(即期望)就是这个分布产生的信息量的平均值(即熵)。
熵的定义:

熵可以理解为不确定性的量度(或者说是多样性diversity的度量),因为越随机的信源的熵越大。熵可以被视为描述一个随机变量的不确定性的数量。一个随机变量的熵越大,它的不确定性越大。那么,正确估计其值的可能性就越小。越不确定的随机变量越需要大的信息量用以确定其值。
熵的单位
单位取决于定义用到对数的底。当b = 2,熵的单位是bit;当b = e,熵的单位是nat;而当b = 10,熵的单位是 Hart。
熵的取值范围
从定义式,我们可以看出,虽然信息熵经常被称为负熵,但是其取值恒为正,这是因为pi恒小于1。不过,由于信息的接受就是不肯定性的消除,即熵的消除(此处的熵取“热力学熵”中“熵”的含义),所以信息熵才常被人称作负熵。熵的取值范围为[0~lgK]。
在概率归一化的限制下,使用拉格朗日乘数法可以找到熵的最大值。因此,我们要最大化
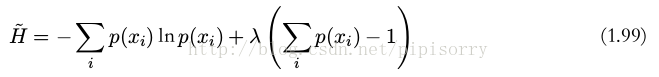
可以证明,当所有的 p(x i ) 都相等,且值为 p(x i ) = 1/M 时,熵取得最大值(当且仅当X的分布是均匀分布时右边的等号成立。即当X服从均匀分布时,熵最大)。其中, M 是状态 x i 的总数。此时对应的熵值为 H = ln M 。这个结果也可以通过 Jensen 不等式推导出来。
熵的特性
- 连续性
- 对称性
- 极值性
- 可加性
- 进一步性质
微分熵(对于连续变量)
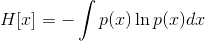
交叉熵(cross entropy)
如果一个随机变量 X ~ p(x),q(x)为用于近似 p(x)的概率分布,那么,随机变量 X 和模型 q 之间的交叉熵定义为:
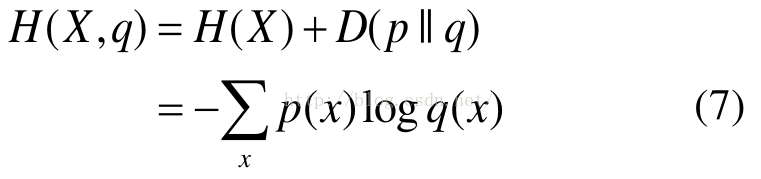
交叉熵的概念用以衡量估计模型与真实概率分布之间的差异
即 p(x)是未知的真实分布,q(x)=估计模型,知其分布用来近似真实分布,我们需要q(x)尽可能地接近p(x),这就是交叉熵最小化
当q(x)=p(x)时,交叉熵=信息熵
相对熵(relative entropy, 或称 Kullback-Leiblerdivergence, KL 距离)
考虑某个未知的分布 p(x) ,假定我们已经使用一个近似的分布 q(x) 对它进行了建模。如果我们使用 q(x) 来建立一个编码体系,用来把 x 的值传给接收者,那么,由于我们使用了 q(x) 而不是真实分布 p(x) ,因此在具体化 x 的值(假定我们选择了一个高效的编码系统)时,我们需要一些附加的信息。我们需要的平均的附加信息量(单位是 nat )为
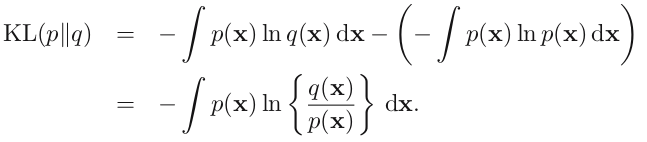
同时,从这可以看出,只有p(x)的积分是一个定值,所以比较不相似度时也可以去掉第二项,就发现第一项其实就是交叉熵!交叉熵实际上是更广泛的相对熵的特殊情形

可以把 Kullback-Leibler 散度(KL 散度之所以不说距离,是因为不满足对称性和三角形法则)。看做两个分布 p(x) 和 q(x) 之间不相似程度的度量。相对熵常被用以衡量两个随机分布的差距。当两个随机分布相同时,其相对熵为0。当两个随机分布的差别增加时,其相对熵也增加。当q=p时,该度量的结果是0,而其它度量的结果为正值。直观上,它度量了使用q而不是p的压缩损失(以二进制)的程度。

假设数据通过未知分布 p(x) 生成,我们想要对 p(x) 建模。我们可以试着使用一些参数分布 q(x | θ) 来近似这个分布。 q(x | θ) 由可调节的参数 θ 控制(例如一个多元高斯分布)。一种确定 θ 的方式是最小化 p(x) 和 q(x | θ) 之间关于 θ 的 Kullback-Leibler 散度。我们不能直接这么做,因为我们不知道 p(x) 。但是,假设我们已经观察到了服从分布 p(x) 的有限数量的训练点 x n ,其中 n = 1, . . . , N 。那么,关于 p(x) 的期望就可以通过这些点的有限加和,使用公式(1.35)来近似,即
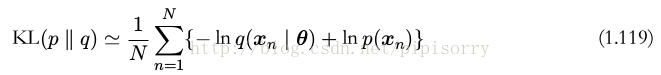
公式(1.119)右侧的第二项与 θ 无关,第一项是使用训练集估计的分布 q(x | θ) 下的 θ 的负对数似然函数。因此我们看到,最小化 Kullback-Leibler 散度等价于最大化似然函数。
相对熵=交叉熵-信息熵