图论------Bellman-Ford算法求单源最短路径的优化

前情回顾：

画图分析：

具体代码：

前情回顾：

大家是否还记得我们之前讲过的Bellman-Ford算法，如果忘记的话可以点击链接去复习一下：图论------贝尔曼-福德（Bellman-Ford）算法-CSDN博客

当时我们是通过画图打表格来讲解的，但是最后代码输出的结果和我给的数据略有差距，这是因为我们是想要将这个数据当作无向图的数据来处理的，但是当时我给到的代码是用来处理有向图的，那我们该怎么办，将u,v,w数据扩展两倍反向再次储存一次边吗？实际上没必要，我们要做的就是多添加两行代码。

画图分析：

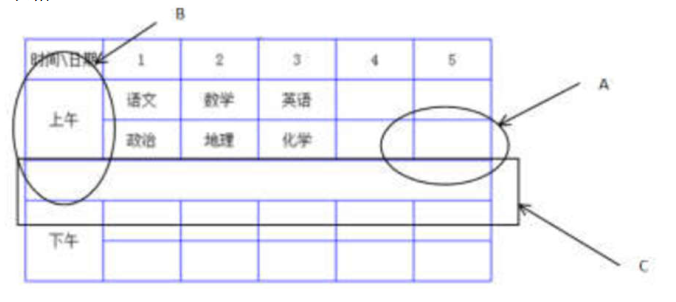
首先大家请看下图：

我们能看到图中存在 2 4 3这一条数据，那么代码运行时一定会有:

if( dic[ 4 ] > dic[ 2 ] + 3) 这一条，显然不成立，因为 dic[ 2 ] = 8，所以无法成立，无法优化1 到 4 的值，然后我们再来看 1 到 2 能不能优化，发现 dic[ 2 ] = dic[ 1 ] + 8无法优化，如果通过 2 4 3这条边能不能优化1 到 2的值呢？我们发现好像不可以哎，因为在之前的代码中的视角，这是个有向图，可惜，如果是无向图就好了，我们会想该怎么调整代码让代码将数据当作无向图处理呢？比如

2 4 3 也可以当作 4 2 3 处理。

当然是可以的，接下来我要讲的东西有点抽象：

大家想一想，在之前代码的认知中w[ i ]是不是有向的，那是因为u[ i ] -->v[ i ]这条边我们只使用了一次，以 2 4 3 这条数据为例：

第一次使用是判断是否 dic[ 4 ] > dic[ 2 ] + 3 意思是 1 到 4 能不能通过 1 -> 2 -> 4来更新，那么如何第二次将2 -> 4 这条边当作 4 -> 2 来使用呢？就是if(dic[ 2 ] > dic[ 4 ] +3)，意思是是否能通过 1 -> 4 -> 2来更新 1到 2的值，如果每条边都那么处理两次，相当于将该图当作无向图处理，因为每条边都正反处理了两次。

具体代码：

#include<stdio.h>
int main(void)
{
   int u[10], v[10], w[10];
   int n, m, inf = 99999999;
   int dic[10] = { 0 };

   scanf("%d%d", &n, &m);
   for (int i = 1; i <= m; i++)
       scanf("%d%d%d", &u[i], &v[i], &w[i]);

for (int i = 2; i <= n; i++)
dic[i] = inf;

   for (int k = 1; k <= n - 1; k++)
       for (int i = 1; i <= m; i++)
           if (dic[v[i]] > dic[u[i]] + w[i])
               dic[v[i]] = dic[u[i]] + w[i];
           else if (dic[u[i]] > dic[v[i]] + w[i])
               dic[u[i]] = dic[v[i]] + w[i];

for (int i = 1; i <= n; i++)
printf("%d ", dic[i]);
}

那么如果所有的路径都已经优化完成了怎么样退出循环呢？

#include<stdio.h>

int main(void)

{

int u[10], v[10], w[10];

int n, m, inf = 99999999;

int dic[10] = { 0 };

scanf("%d%d", &n, &m);

for (int i = 1; i <= m; i++)

scanf("%d%d%d", &u[i], &v[i], &w[i]);

for (int i = 2; i <= n; i++)