title: 希尔排序
date: 2024-7-25 10:48:15 +0800
categories:
- 排序算法
tags: - 排序
- 算法
- 希尔排序
description: 1959年Shell发明,是简单插入排序的改进版。是一种高效的排序算法,通过分组和逐步缩减增量,使得数组在接近有序的情况下进行最终排序,从而提高效率。
math: true
希尔排序
希尔排序(Shell Sort)是一种基于插入排序的排序算法,通过优化插入排序中的比较和移动操作,实现更高效的排序。希尔排序通过将数组分成若干子序列分别进行插入排序,使得数据项的步长逐渐减少,最终进行一次普通的插入排序。本文将详细介绍希尔排序的原理、步骤、示例、复杂度分析及其Java代码实现。
希尔排序的原理
- 分组:将待排序数组按某个增量分组,对每组分别进行插入排序。
- 缩减增量:逐步缩减增量,重复上述分组和排序过程。
- 最终排序:当增量缩减为1时,对整个数组进行一次普通的插入排序。
希尔排序通过多次分组和排序,使得数组在接近有序的情况下进行最终排序,从而提高效率。
希尔排序的步骤
- 选择初始增量:选择一个较大的初始增量(一般为数组长度的一半)。
- 分组并插入排序:按当前增量将数组分组,对每组分别进行插入排序。
- 缩减增量:将增量减半,重复分组和排序过程。
- 最终排序:当增量缩减为1时,对整个数组进行一次插入排序。
图示
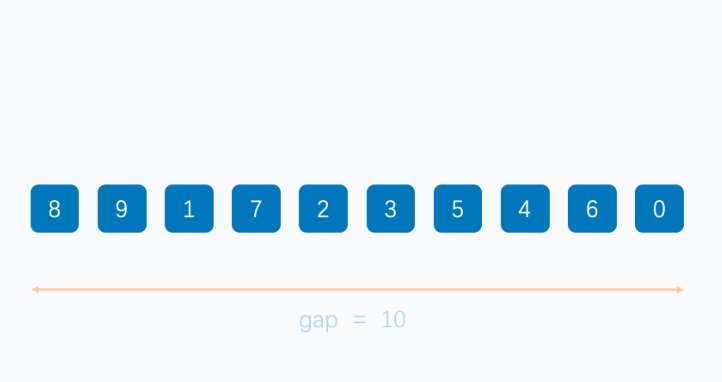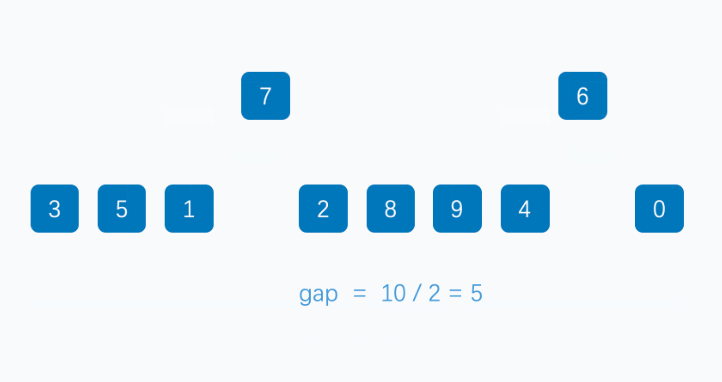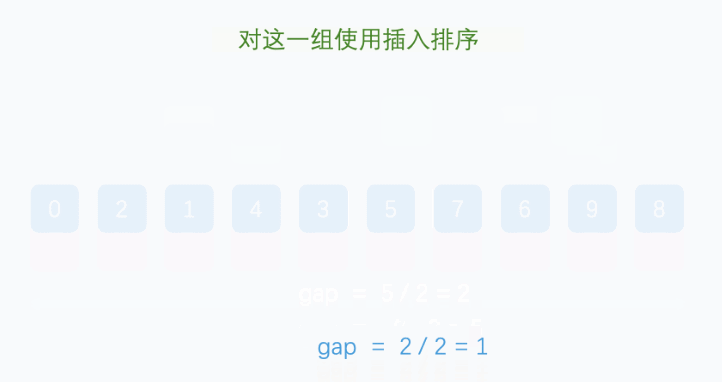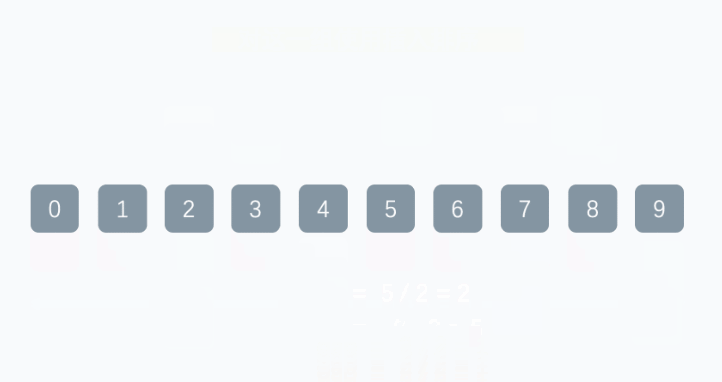
示例

步长
-
Shell 的原始序列: N 2 \frac{N}{2} 2N, N 4 \frac{N}{4} 4N , …, 1 (重复除以 2);
-
Hibbard 增量: 1, 3, 7, …, 2 k − 1 2^k-1 2k−1 ;
-
Knuth 增量: 1, 4, 13, …, ( 3 k − 1 ) 2 \frac{(3^k-1)}{2} 2(3k−1) ;
-
Sedgewick 增量: 1, 5, 19, 41, 109, …
它是通过将两个序列的元素交织得到的:1, 19, 109, 505, 2161,……, 9 ( 4 k – 2 k ) + 1 9(4^k–2^k)+1 9(4k–2k)+1, k = 0, 1, 2, 3,…
5, 41, 209, 929, 3905,…… 2 k + 2 ( 2 k + 2 – 3 ) + 1 2^{k+2}(2^{k+2}–3)+1 2k+2(2k+2–3)+1, k = 0, 1, 2, 3, …
复杂度分析
步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序,最终算法以步长为1进行排序。当步长为1时,算法变为普通插入排序,这就保证了数据一定会被排序。
Donald Shell最初建议步长选择为 n 2 \frac {n}{2} 2n并且对步长取半直到步长达到1。虽然这样取可以比 O ( n 2 ) O(n^{2}) O(n2)类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。
| 步长序列 | 最坏情况下复杂度 |
|---|---|
| n 2 i \frac {n}{2^{i}} 2in | O ( n 2 ) O(n^{2}) O(n2) |
| 2 k − 1 2^{k}-1 2k−1 | O ( n 3 2 ) O(n^{\frac {3}{2}}) O(n23) |
| 2 i 3 j 2^{i}3^{j} 2i3j | O ( n log 2 n ) O(n\log ^{2}n) O(nlog2n) |
已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,…)。“比较在希尔排序中是最主要的操作,而不是交换。”用这样步长序列的希尔排序比插入排序要快,甚至在小数组中比快速排序和堆排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
另一个在大数组中表现优异的步长序列是斐波那契数列除去0和1将剩余的数以黄金分割比的两倍的幂进行运算得到的数列:(1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713,…)
时间复杂度
- 最佳情况: O ( n log 2 n ) O(n \log^2 n) O(nlog2n)
- 最坏情况: O ( n 2 ) O(n^2) O(n2)
- 平均情况: O ( n 1.3 ) O(n^{1.3}) O(n1.3)。
空间复杂度
- 空间复杂度: O ( 1 ) O(1) O(1)。
希尔排序的代码实现(Java)
public class ShellSort {// 主排序函数public static void shellSort(int[] arr) {int n = arr.length;// 选择初始增量for (int gap = n / 2; gap > 0; gap /= 2) {// 按增量进行插入排序for (int i = gap; i < n; i++) {int temp = arr[i];int j;// 插入排序for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}}}// 主函数public static void main(String[] args) {int[] arr = {38, 27, 43, 3, 9, 82, 10};System.out.println("Given Array:");for (int num : arr) {System.out.print(num + " ");}System.out.println();// 调用希尔排序函数shellSort(arr);System.out.println("\nSorted Array:");for (int num : arr) {System.out.print(num + " ");}System.out.println();}
}