以老虎机为例介绍各算法
import numpy as np#每个老虎机的中奖概率,0-1之间均匀分布
probs = np.random.uniform(size=10)#生成一个数组,其中的元素是从均匀分布(也称为矩形分布)中随机抽取的。均匀分布意味着每个数出现的概率是相同的。#记录每个老虎机的返回值
rewards = [[1]for _ in range(10)] #初始化为1probs,rewards
import random
#贪婪算法的改进,递减的贪婪算法
def choose_one():#求出现在已经玩了多少次played_count = sum([len(i) for i in rewards])#随机选择的概率逐渐下降if random.random()<1/played_count:return random.randint(0,9)#计算每个老虎机的奖励平均rewards_mean = [np.mean(i) for i in rewards]#选择期望奖励估计值最大的拉杆return np.argmax(rewards_mean)
choose_one()def try_and_play():i = choose_one()#玩老虎机,得到结果reward = 0if random.random()<probs[i]:reward = 1#记录玩的结果rewards[i].append(reward)try_and_play()
rewards
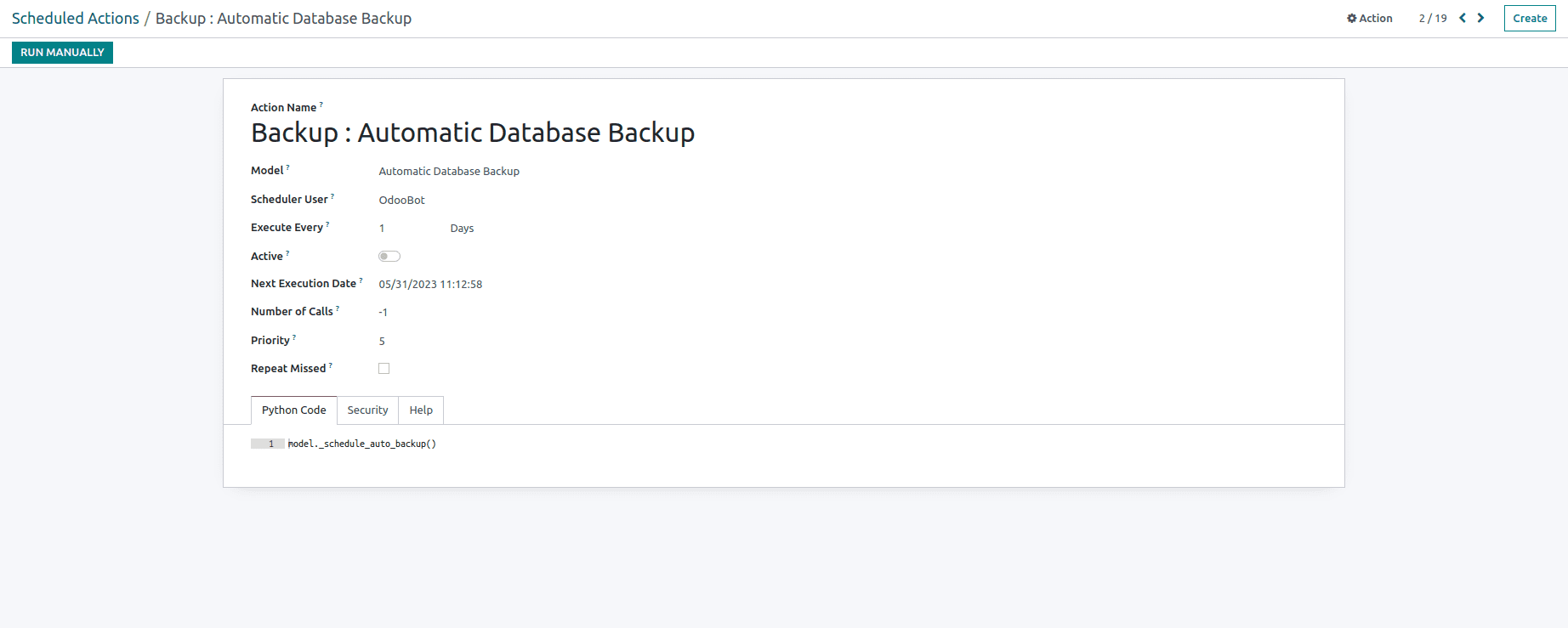
def get_result():#玩N次for _ in range(5000):try_and_play()#期望的最好结果target = probs.max()*5000#实际玩出的结果result = sum([sum(i) for i in rewards])return target,resultget_result()#前面是拿老虎机中奖概率最高的那台玩5000次出来的结果(理想上的最好)![]()
上置信界算法UCB算法,多探索玩的少的机器
上置信界(Upper Confidence Bound, UCB)是一种用于决策过程中评估和比较不同选择的方法,特别是在面对不确定性时。UCB 通常与多臂老虎机问题(Multi-Armed Bandit Problem)相关,这是一种用以描述在不确定性下如何做出最优选择的理论框架

import random #随机选择的概率递减的贪婪算法
def choose_one():#求出每个老虎机各玩了多少次played_count = [len(i) for i in rewards]played_count = np.array(played_count)#求出上置信界#分子是总共玩了多少次,取根号后让他的增长速度变慢#分母是每台老虎机玩的次数,乘2让他的增长速度变快#随着玩的次数增加,分母会很快超过分子的增长速度,导致分数越来越小#具体到每一台老虎机,则是玩的次数越多,分数就越小,也就是ucb的加权越小#所以ucb衡量了每一台老虎机的不确定性,不确定性越大,探索的价值越大fenzi = played_count.sum()**0.5fenmu = played_count*2ucb = fenzi/fenmu#ucb本身取根号#大于1的数会被缩小,小于1的数会被放大,这样保持ucb恒定在一定的数值范围内ucb = ucb**0.5#计算每个老虎机奖励平均rewards_mean = [np.mean(i) for i in rewards]rewards_mean = np.array(rewards_mean)#ucb和期望求和ucb+=rewards_meanreturn ucb.argmax()def try_and_play():i = choose_one()#玩老虎机,得到结果reward = 0if random.random()<probs[i]:reward = 1#记录玩的结果rewards[i].append(reward)try_and_play()
def get_result():#玩N次for _ in range(5000):try_and_play()#期望的最好结果target = probs.max()*5000#实际玩出的结果result = sum([sum(i) for i in rewards])return target,resultget_result()#前面是拿老虎机中奖概率最高的那台玩5000次出来的结果(理想上的最好)
汤普森采样法
汤普森采样(Thompson Sampling)是一种用于解决多臂老虎机问题(Multi-Armed Bandit Problem)的贝叶斯启发式方法。它是一种概率性的方法,通过随机选择最佳选项来平衡探索(exploration)和利用(exploitation)之间的权衡。以下是汤普森采样的一些关键特点:
-
贝叶斯方法:汤普森采样基于贝叶斯定理,通过假设奖励分布的先验知识,并根据观察到的数据更新这个分布。
-
随机性:与确定性的贪婪策略不同,汤普森采样在每次选择时都引入随机性,这有助于探索不太熟悉的选项。
-
探索与利用:汤普森采样自然地结合了探索(尝试新的或较少选择的选项)和利用(选择当前看起来最佳的选项)。
-
实现步骤:
- 对每个选项,根据其历史数据定义一个概率分布(通常是Beta分布或Beta二项分布)。
- 在每次选择时,从每个选项的概率分布中抽取一个样本。
- 选择具有最高样本值的选项进行探索。
-
适用场景:汤普森采样适用于奖励分布未知且需要不断学习的场景。
-
数学表达:如果假设奖励是从一个Beta分布中抽取的,那么在选择了n次之后,其中w次获得成功,Beta分布的参数将更新为
(α = w + 1, β = n - w + 1)。
#beta分布测试,你正在生成一个具有参数 α=1 和 β=1 的 Beta 分布的随机数。当 α=1 且 β=1 时,Beta 分布退化为均匀分布,这意味着生成的随机数将在 [0, 1] 区间内几乎均匀地分布。
print('当数字小的时候,beta分布的概率有很大的随机性')
for _ in range(5):print(np.random.beta(1,1))
print('当数字大时,beta分布逐渐稳定')
for _ in range(5):print(np.random.beta(1e5,1e5))
import random
def choose_one():#求出每个老虎机出1的次数+1count_1 = [sum(i)+1 for i in rewards]#求出每个老虎机出0的次数+1count_0 = [sum(1-np.array(i))+1 for i in rewards]#按照beta分布计算奖励分布,这可以认为是每一台老虎机中奖的概率beta = np.random.beta(count_1,count_0)return beta.argmax()choose_one()def try_and_play():i = choose_one()#玩老虎机,得到结果reward = 0if random.random()<probs[i]:reward = 1#记录玩的结果rewards[i].append(reward)try_and_play()
def get_result():#玩N次for _ in range(5000):try_and_play()#期望的最好结果target = probs.max()*5000#实际玩出的结果result = sum([sum(i) for i in rewards])return target,resultget_result()#前面是拿老虎机中奖概率最高的那台玩5000次出来的结果(理想上的最好)(4965.406675195595, 4971)


![[Linux][OS][信号的保存和处理]](https://img-blog.csdnimg.cn/img_convert/65df0a3f703881d478d3227e5bbccd6e.jpeg)