A Tutorial to SAT Solving 约束求解基础与应用4.10
1. SAT的概念
Propositional Satisfiability (SAT):Given a propositional formula φ, test whether there is an assignment to the variables that makes φ true.
公式组成:
- 布尔变量x literal:a Boolean variable 𝑥 (positive literal) or its
- negation ¬𝑥 (negative literal)
- clause:literals的析取disjunction(V)、CNF合取范式
Every propositional formulas can be converted into CNF efficiently.
MaxSAT:When the formula is not satisfiable, we concern about satisfying as many clauses as possible -> Maximum Satisfiability
当公式不可满足时,我们关心的是尽可能多地满足子句 -> 最大可满足性

MaxSAT的变体:
weighted maxsat:每个子句都关联一个权重,目标:最大化满足子句的总权重
partial maxsat:包含hard clauses(必须满足的子句)和soft clauses(尽可能多满足),目标:满足所有硬从句和尽可能多的软从句。
weighted partial maxsat:每个soft clause关联一个权重,目标:满足所有的hard子句和最大化软子句的总权重
*Example:*MaxClique Problem
求解问题的关键时对问题进行编码,用SAT思路编码。
2. Solvers 求解器
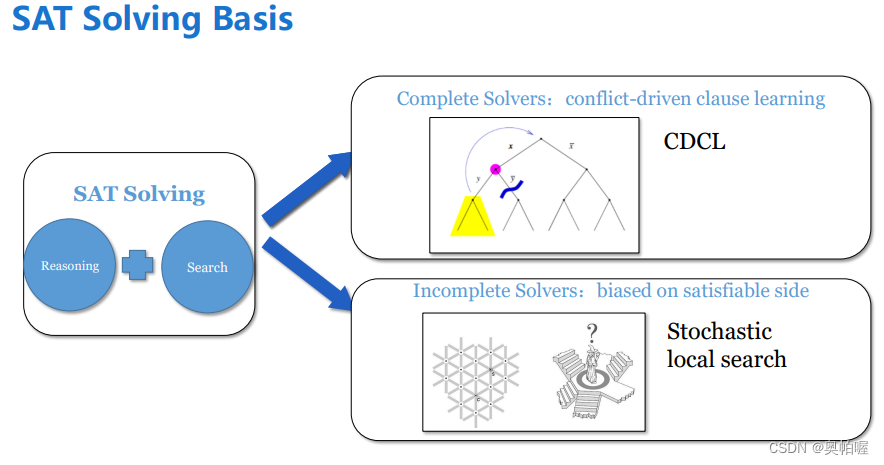
求解SAT两大思路:推理reasoning和搜索search。求解器又分为完备的和不完备的。
SAT Solving Basis
- Resolution 归结:可以消除变量
由CVx和非xVD可以得到CVD,变量x消失
找到变量的正出现和负出现,做归结 - Unit Propagation 单元传播
Unit Clause:子句中只有一个变量或者,如果一个子句里面,其它字母都导出"假",只剩一个字母了,这个子句叫单元子句,这个子句必须设置为真
传播的过程是一步步递进的,一个字母指定为T,会导致其他子句成为单元子句,就可以推出其他字母的真值。
DPLL Algorithm
Chronological backtracking + UP + Decision heuristics时间顺序回溯+单元传播+决策启发式
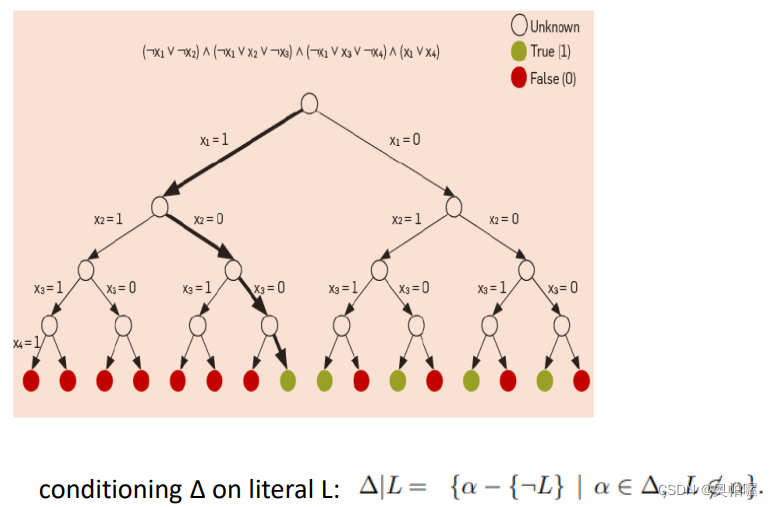
原始结点是一个公式,对一个变量取真值,就可以对公式化简,变成一个子公式,如果x1取1,那么最后一个子句x1x4满足,非x1也可以化掉;最后只要一条路径可以通道叶子节点,公式就成立。不可满足的话,就需要搜索整个空间。
example: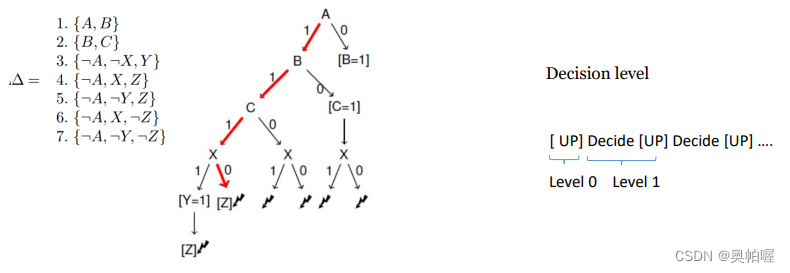
类似于深度优先搜索,只要遇到冲突,就回溯到上一层。先做单元传播,之后选一个分支即decide决策,算法需要decide哪个分支,有可能没有UP,所以有括号。UP和Decide迭代进行。
Decision level:由Decide开启,之后是UP,两者在一层。
Lazy data structure for UP
UP很耗时间,先判断单元子句,改进:
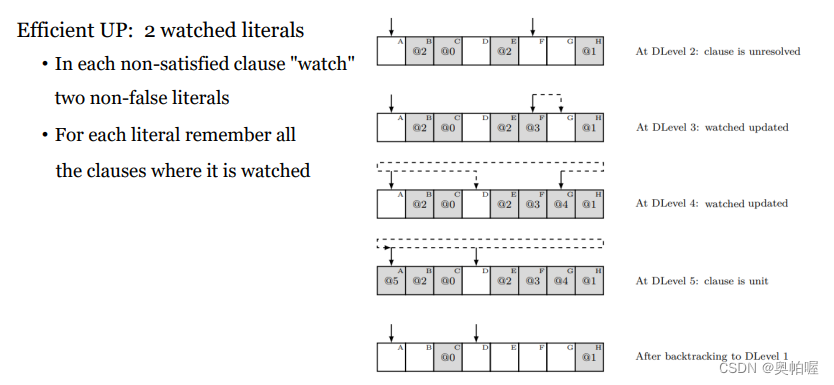
每个clause设置两个变量为watched literal,随着赋值迭代,若其中一个变量被赋值了,就找新的未被赋值的变量,直到只剩下一个watched literal,也就是只有一个变量未被赋值,那这个clause就是单元子句了。
VSIDS Branching heuristics分支启发式
• Branching heuristics are used for deciding which variable to use when branching.
• Solvers prefer the variable which may cause conflicts faster.
• Variable State Independent Decaying Sum (VSIDS) [MoskewiczMadiganZhaoZhangMalik’01]
• Compute score for each variable, select variable with highest score
• Initial variable score is number of literal occurrences.
• For a new conflict clause 𝑐: score of all variables in 𝑐 is incremented.
• Periodically, divide all scores by a constant. // forgetting previous effects
回溯搜索是一个比较连续型的搜索,近期之内经常发生冲突的话,可以预测将来也会发生冲突,类似操作系统中程序连续性行为。
• Most popular: the exponential variant in MiniSAT (EVSIDS)
• The scores of some variables are 𝑏𝑢𝑚𝑝𝑒𝑑 with 𝑖𝑛𝑐, and 𝑖𝑛𝑐 decays after each conflict.
• Initialize 𝑠𝑐𝑜𝑟𝑒 to 0, the bump score 𝑖𝑛𝑐 default to 1.
• 𝑖𝑛𝑐 multiply 1/𝑑𝑒𝑐𝑎𝑦 after each conflict, 𝑑𝑒𝑐𝑎𝑦 initialized to 0.8, increased by 0.01 every [5k] conflicts, the maximum of 𝑑𝑒𝑐𝑎𝑦 is 0.95.
• The score of variables in conflict clause 𝑐 are bumped with 𝑖𝑛𝑐
Backjumping回跳多层
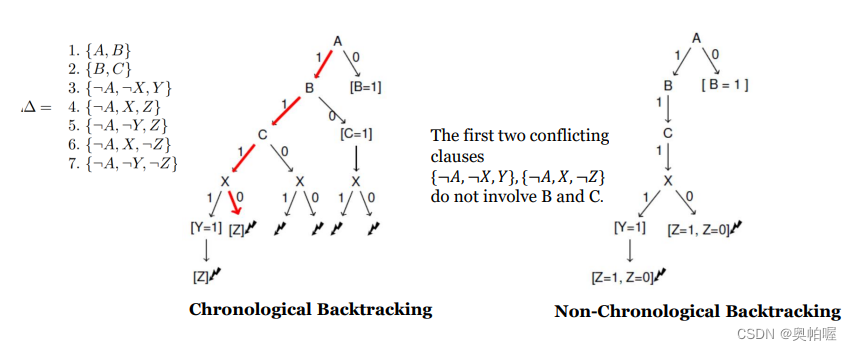
如果回溯到B或者C层是没用的,应该直接回跳到A层。
回跳只是找到了冲突的变量,如果可以继续分析出冲突的原因,就可以省略更多的搜索空间
CDCL: Conflict Driven Clause Learning子句学习**

Implication Graph有向无环图