以前看地球物理教材的时候，经常碰到和卷积和傅里叶变换，一看到卷积或者反卷积就头大，直接跳过去，至于傅里叶变换，由于有高数的基础，明白它是将时域变换成频率域的公式。最近要用matlab对时域信号进行频谱分析，说人话就是将采集的重力或磁力数据傅里叶变换成频率数据，然后对其分析，看数据是否有滤波。

 

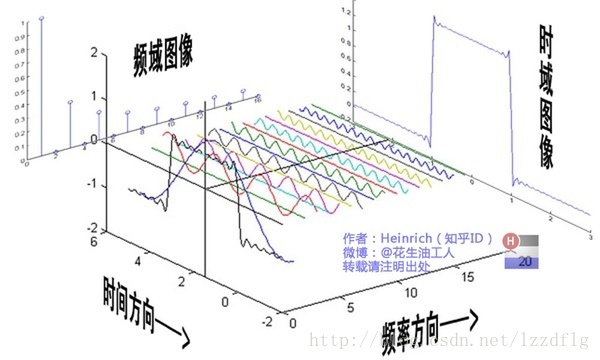
因为卷积重要的应用领域就是信号处理，卷积定理将时间域或空间域中的卷积运算等价为频率域的相乘运算，利用傅里叶等快速算法，实现有效的计算，节省运算代价，所以，硬着头皮看了一些相关的教程和解释。

根据百度百科，卷积、旋积或褶积(Convolution)是通过两个函数f和g生成第三个函数的一种数学运算，其本质是一种特殊的积分变换，表征函数f与g经过翻转和平移的重叠部分函数值乘积对重叠长度的积分。卷积是一种线性运算（加法和数量乘法），满足交换律、结合律、分配律等。

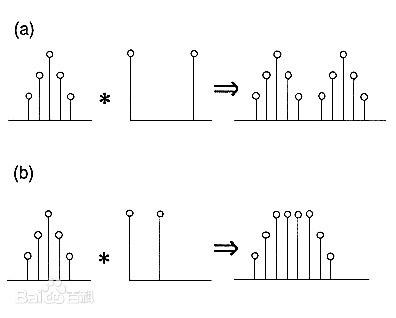
那么卷积究竟是个啥，个人感觉与滤波的意思差不多，如果按照滤波理解，卷积就显得通俗易懂。下面这张图表面说的是卷积和滤波的区别，但实际上更说明它俩原理相通。

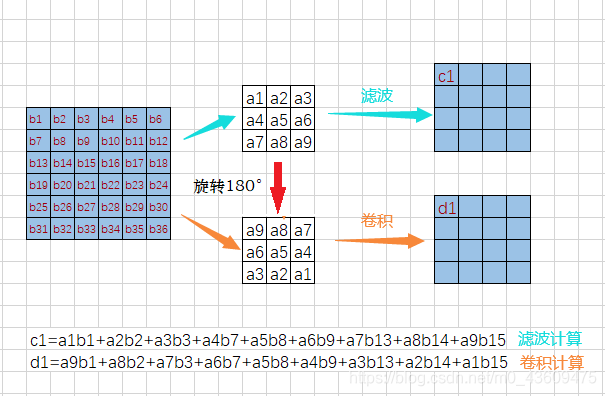
再说一个卷积应用比较多的领域，就是地震勘探。在地震勘探中，在地表激发点激发的地震子波(seismic wavelet)向地下传播，当遇到地下波阻抗界面时，一部分能量就会作为反射地震波向上反射回地表，被地面的传感器接收，随着地震波不断向下传播、反射、接收,就会记录一系列时间延迟的地震波(大地滤波后的地震子波)，称为地震记录（时域信号）。

如果假设地下介质为古皮奥(Goupilaud)的水平层状介质模型，子波为雷克(Ricker)子波，地震记录可以看作是由震源子波与地下反射率函数、多次反射、仪器等诸多因素的相卷积的过程，令x(t)、w(t)和n(t)分别表示地震记录、地震子波及杂波，卷积过程数学模型描述为

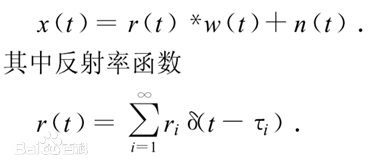
反卷积算法就是求反射函数w(t)，可用来消除二次波。

不过，说了这么多，可能对我们运用matlab进行信号处理没什么用。下面进入正题。

时域数据：磁力仪的静态和动态采集数据

信号分析工具：Matlab2014a的Signal Analysis

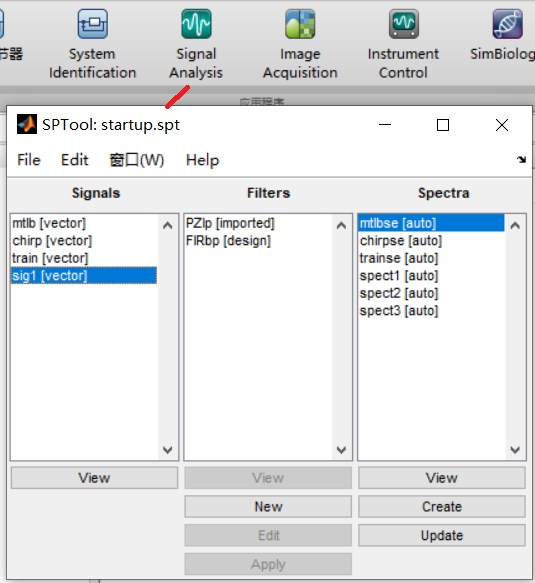
打开G882的静态数据（时域信号），频率10Hz（1秒采集10个数），时长大约12小时。

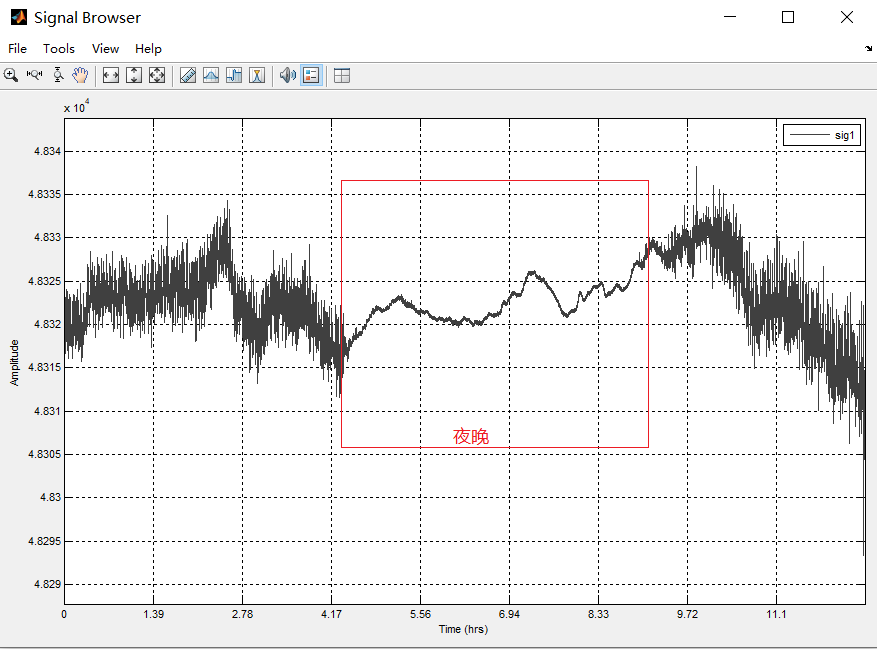
再看这段数据的功率谱。说老实话，看不懂，看不出来有没有滤波。据有经验的老师说，这个可能做了一个<3Hz的低通滤波（保留小于3Hz的数据）。

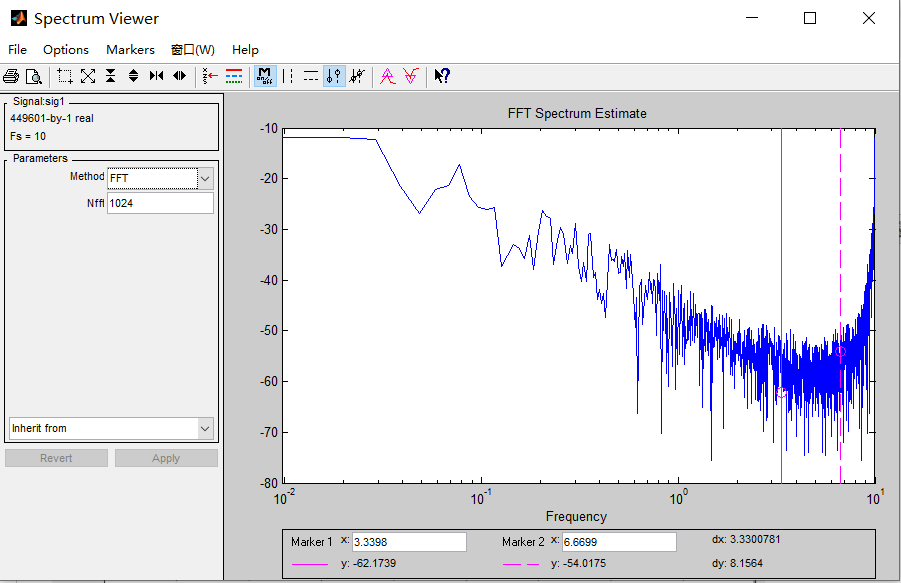
打开G882的动态数据（时域信号），频率10Hz（1秒采集10个数），时长大约0.5小时。

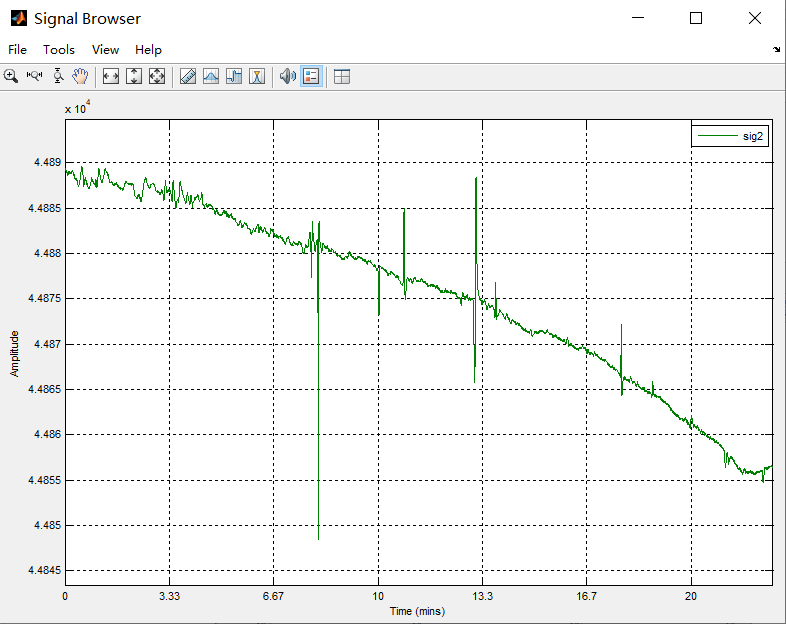
再看这段数据的功率谱。静态数据和动态数据的频谱不一样，不一样地方主要在红圈内。据有经验的老师说，这个可能做了一个3Hz~5Hz的带阻滤波或陷波（过滤3Hz~5Hz的数据）。

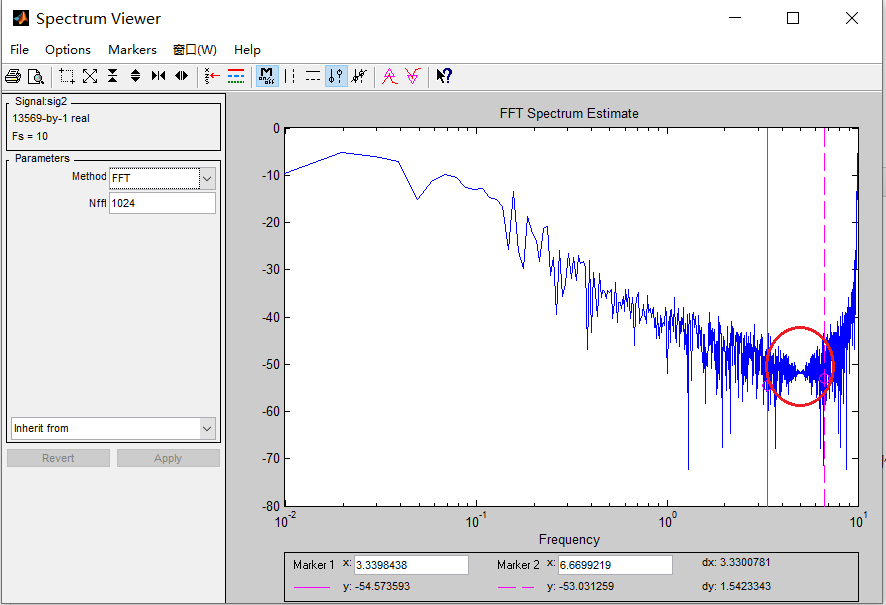
参考文献

https://www.bilibili.com/video/BV15V4y1x7ge/?vd_source=6f9f0ad1eef623c5a58999f0093952a1

https://www.bilibili.com/video/BV1Vd4y1e7pj/?spm_id_from=333.880.my_history.page.click&vd_source=6f9f0ad1eef623c5a58999f0093952a1

https://blog.csdn.net/chief_cf/article/details/78691950

https://blog.csdn.net/daduzimama/article/details/80182108

https://blog.csdn.net/sy243772901/article/details/124112288

https://blog.csdn.net/Simon223/article/details/119894882

https://www.cnblogs.com/allen-blog/articles/17492628.html

https://blog.csdn.net/m0_43609475/article/details/112447397

https://baike.baidu.com/item/%E5%8D%B7%E7%A7%AF/9411006

https://blog.csdn.net/lzzdflg/article/details/78254381