股票买卖题型详解

股票买卖题型

买卖股票最佳时机

在这里插入图片描述

第一题贪心算法应该快很多就不讲。此类问题思路大致一致

在这里插入图片描述

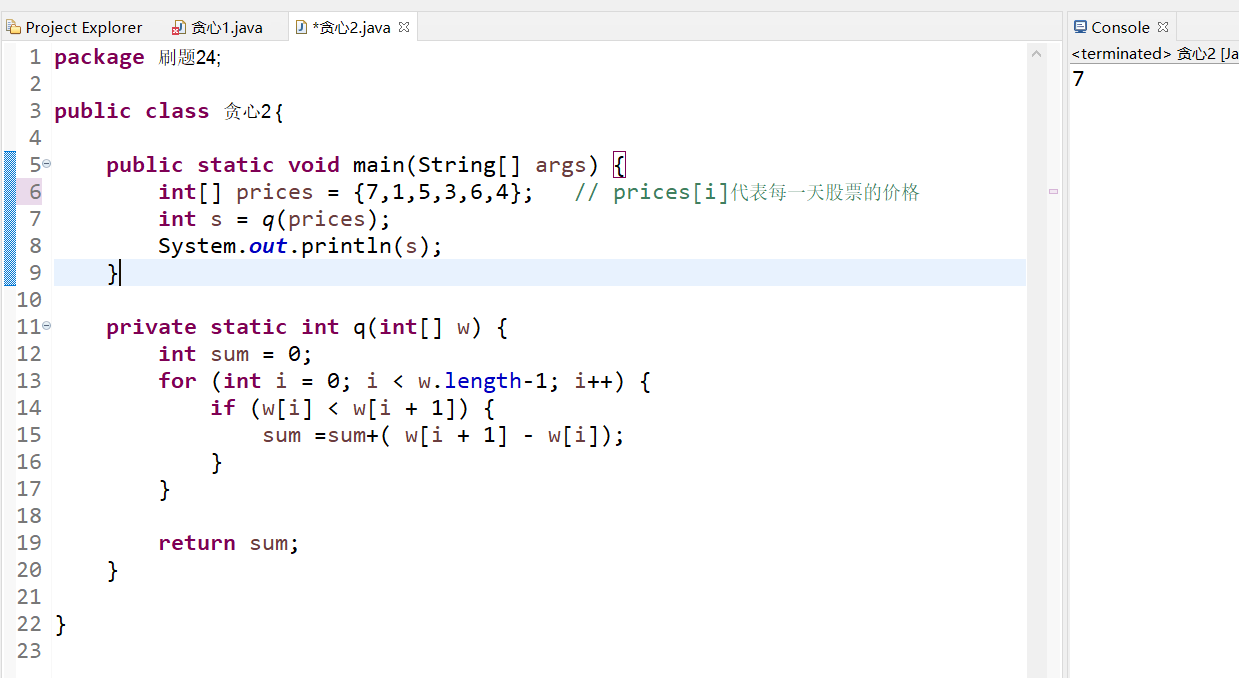
第二题也可用贪心做 ans =max(ans, ans+prices[i]-prices[i-1]);

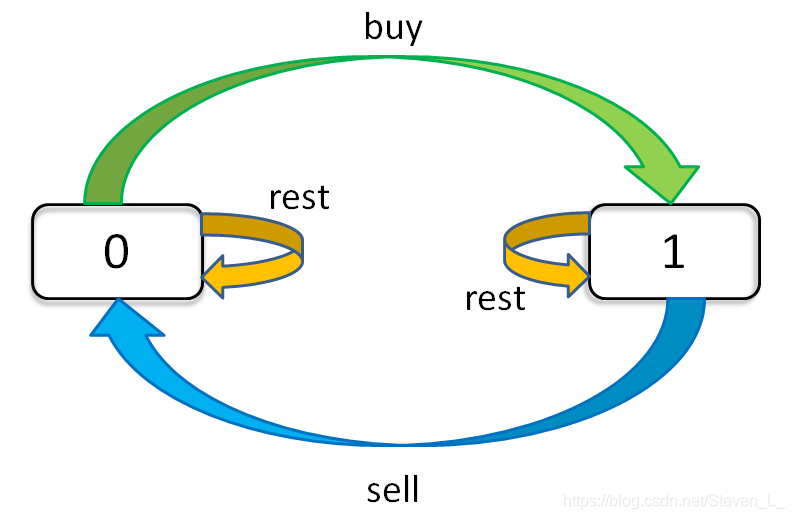
分析： 共有两个属性值， 未持有 和持有股票

定义 f[ i ] [ 2 ] f[ i ] [ 0 ]表示第i 天的未持有股票的最大收益。分为卖股票和保持之前状态，所以
$f [i] [0] = m a x (f [i - 1] [0], f [i - 1] [1] + p r i c e s [i])$
f[ i ] [ 1 ] 表示第 i 天的持有股票的最大收益。分为购买股票和继续持有之前的股票，所以
$f [i] [1] = m a x (f [i - 1] [1], f [i - 1] [0] - p r i c e s [i])$

public  int maxProfit(int[] prices) {int n = prices.length;if(n < 2 ) return 0;int f[][]= new int[n+1][2];f[0][0] = 0;f[0][1] = -prices[0];for(int i  =1 ;  i < n ; ++i){f[i][0] = Math.max(f[i-1][0],f[i-1][1]+prices[i]);f[i][1] = Math.max(f[i-1][1],f[i-1][0]-prices[i]);}return f[n-1][0];}

优化： 发现 f[i] [0] || f[i] [1] 仅和前一天的状态有关，因此用滚动数组进行优化

定义一个最小花费ans[1] 替代 f[ i ] [ 1 ] , ans[0] 替代f[ i ] [ 0 ]

public  int maxProfit(int[] prices) {int n = prices.length;int f[]= new int[2];f[0] = 0;f[1] = -prices[0];for(int i  = 1 ;  i < n ; ++i){f[0] = Math.max(f[0],f[1]+prices[i]);f[1] = Math.max(f[1],f[0]-prices[i]);}return f[0];}

当进行限制交易次数：

在这里插入图片描述

沿用之前分析思路：

再增加一个维度第k次交易 即：f[ i ] [ 0|1 ] [ 0 | 1 ]

状态转移方程：

第一次交易未持有股票时最大收益：
$f [i] [0] [0] = m a x (f [i - 1] [0] [0], f [i - 1] [1] [0] + p r i c e s [i])$
第一次交易持有股票时最大收益（因为第一笔交易和第二笔交易不能同时进行，所以只需要记录第一次交易的购买最小值在进行计算收益即可）：
$f [i] [1] [0] = m a x (f [i - 1] [1] [0], - p r i c e s [i])$
第二次交易未持有股票时最大收益：
$f [i] [0] [1] = m a x (f [i - 1] [0] [1], f [i - 1] [1] [1] + p r i c e s [i])$
第一次交易持有股票时最大收益：
$f [i] [1] [1] = m a x (f [i - 1] [1] [1], f [i - 1] [0] [0] - p r i c e s [i])$

public int maxProfit(int[] prices) {int n = prices.length;int[][][] f = new int[n][2][2];f[0][1][0] = -prices[0];f[0][1][1] = -prices[0];for (int i = 1; i < n; ++i) {f[i][0][0] = Math.max(f[i-1][0][0],f[i-1][1][0]+prices[i]);f[i][1][0] = Math.max(f[i-1][1][0],-prices[i]);f[i][0][1] = Math.max(f[i-1][0][1],f[i-1][1][1]+prices[i]);f[i][1][1] = Math.max(f[i-1][1][1],f[i-1][0][0]-prices[i]);}return f[n-1][0][1];}

优化： 可以发现第i天的状态只与第i-1天的状态有关，因此可以考虑使用滚动数组进行优化空间

public int maxProfit(int[] prices) {int n = prices.length;int buy1 = -prices[0], sell1 = 0; //  第一次交易int buy2 = -prices[0], sell2 = 0; //  第二次交易for (int i = 1; i < n; ++i) {buy1 = Math.max(buy1, -prices[i]);sell1 = Math.max(sell1, buy1 + prices[i]);buy2 = Math.max(buy2, sell1 - prices[i]);sell2 = Math.max(sell2, buy2 + prices[i]);}return sell2;}

在这里插入图片描述

分析：与第三题相似，只不过再将交易维度从2变成了k维；

以下直接给出优化后的代码：

public int maxProfit(int k, int[] prices) {if(prices.length == 0 || k == 0) return 0;int dp[] = new int[k*2];for(int i = 0 ; i < 2*k ;i+=2){dp[i] = 0;dp[i+1] = -prices[0];}// 每一次的 持有股票定义为 m%2== 1 ， 未持有则为 m%2==0for(int i = 1;  i < prices.length;++i){dp[0] = Math.max(dp[0],dp[1]+prices[i]); // 第一次出售的收益dp[1] =Math.max(dp[1],-prices[i]); // 第一次持有所花的钱for(int j = 2 ; j < 2*k ;j+=2){dp[j] = Math.max(dp[j],dp[j+1]+prices[i]); // 第j次出售的收益dp[j+1] =Math.max(dp[j+1],dp[j-2]-prices[i]);// 持有第j次的股票}}return dp[2*k-2];}

含有冷冻期的买卖股票时机：

在这里插入图片描述

分析：状态转移方程

未持有股票：
$f [i] [0] = m a x (f [i - 1] [2], f [i - 1] [0])$
持有股票：
$f [i] [1] = m a x (f [i - 1] [1], f [i - 1] [0] - p r i c e s [i])$
冷冻期：
$f [i] [2] = f [i - 1] [0] + p r i c e s [i]$

public int maxProfit(int[] prices) {if (prices.length == 0) {return 0;}int n = prices.length;int[][] f = new int[n][3];f[0][1] = -prices[0];for (int i = 1; i < n; ++i) {f[i][0] = Math.max(f[i-1][2],f[i-1][0]);f[i][1] = Math.max(f[i-1][1],f[i-1][0]-prices[i]);f[i][2] = f[i-1][1]+prices[i];}return Math.max(f[n - 1][0], f[n - 1][2]);}

**优化：思路与前几题相似 **是用滚动数组进行空间优化

public int maxProfit(int[] prices) {if(prices.length==0)    return 0;int f1, f2 ,f3 , f4, f5, f6;   // f1 f6 :未持有  f2 f4: 冷冻期  f3 f5: 持有f1 = 0;f2 = 0;f3 = -prices[0];for(int i = 1; i < prices.length;++i){f4 = f3+prices[i];// -1 0  -1 2   0 2  4  f5 = Math.max(f1-prices[i],f3);f6 = Math.max(f2,f1);f2 = f4;f1 = f6;f3 = f5;}return Math.max(f1,f2);}