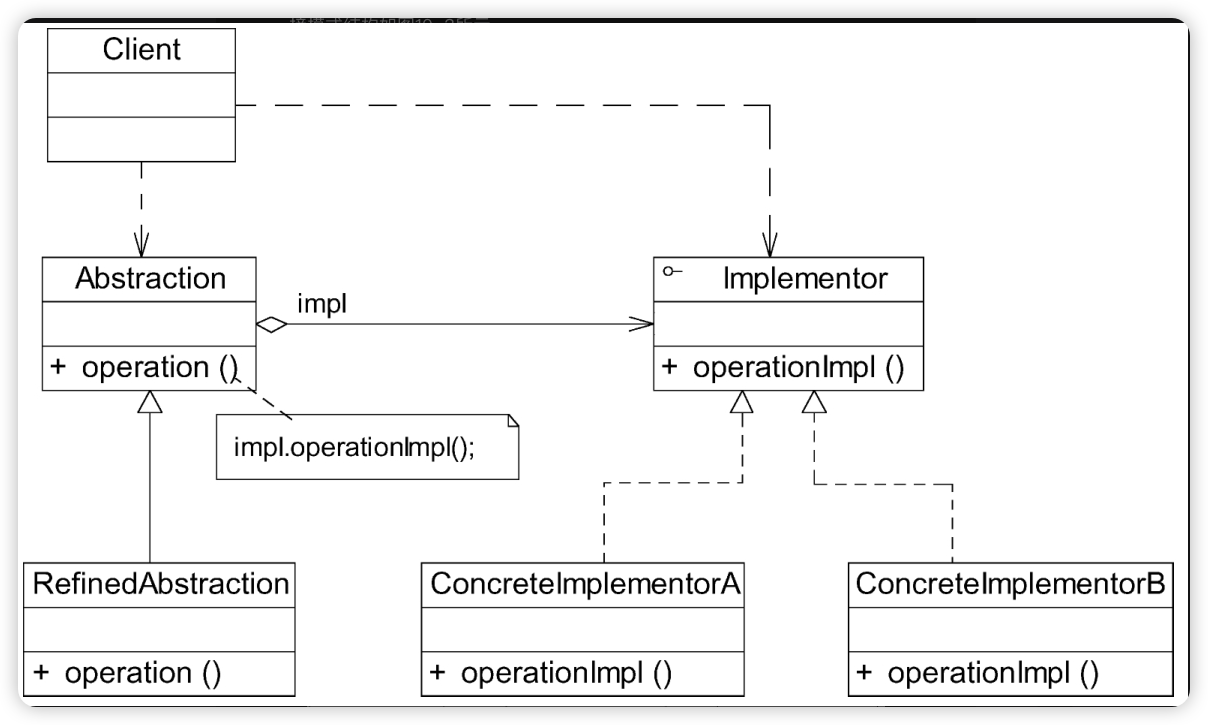
目录

语法

说明

示例

矩阵的条件数

1-范数条件数

---

        cond函数的功能是返回逆运算的条件数。

语法

C = cond(A)
C = cond(A,p)

说明

        C = cond(A) 返回 2-范数逆运算的条件数，等于 A 的最大奇异值与最小奇异值之比。

        C = cond(A,p) 返回 p-范数条件数，其中 p 可以是 1、2、Inf 或 'fro'。

示例

矩阵的条件数

        计算矩阵的条件数并检查逆运算的敏感度。创建一个 2×2 矩阵。

A = [4.1 2.8;9.7 6.6];

        计算 A 的 2-范数条件数。

C = cond(A)
C = 1.6230e+03

        由于 A 的条件数远大于 1，因此矩阵对逆运算非常敏感。计算 A 的逆矩阵，对 A 的第二行进行小小的改动，然后再次进行逆运算。

invA = inv(A)
invA = 2×2-66.0000   28.000097.0000  -41.0000A2 = [4.1    2.8; 9.671  6.608]
A2 = 2×24.1000    2.80009.6710    6.6080invA2 = inv(A2)
invA2 = 2×2472.0000 -200.0000-690.7857  292.8571

        结果表明，对A进行的小小改动可能完全改变逆运算的结果。

1-范数条件数

        计算矩阵的 1-范数条件数。创建一个 3×3 矩阵。

A = [1 0 -2;3 4  6;-1 5  7];

        计算 A 的 1-范数条件数。m×n 矩阵的 1-范数条件数的值为

其中 1-范数是矩阵的最大绝对列之和，由以下公式计算得出：

C = cond(A,1)
C = 18.0000

        对于此矩阵，条件数不是太大，因此矩阵对逆运算不是特别敏感。

逆运算的条件数

        矩阵和计算任务的条件数用于衡量解算过程中答案对输入数据变化和舍入误差的敏感程度。

        矩阵的逆运算的条件数用于测量线性方程组的解对数据错误的敏感程度。它指示矩阵求逆结果和线性方程解的精度。例如，一个方阵的 2-范数条件数是

        在这种情况下，大的条件数表示系数矩阵 A 中的微小变化会导致线性方程 Ax = b 和 xA = b 的输出 b 发生较大变化。极端情况是 A 因过于病态而成为奇异矩阵（无限条件数），此时它没有逆矩阵，而线性方程没有唯一解。

提示

• 与 cond 相比，rcond 作为估计矩阵条件的方法更高效，但不够稳定。

算法

cond 的算法分为三部分：

• 如果 p = 2，则 cond 使用由 svd 提供的奇异值分解来计算最大奇异值和最小奇异值之比。

• 如果 p = 1、Inf 或 'fro'，则 cond 使用输入矩阵及其逆矩阵的适当范数通过 norm(A,p) * norm(inv(A),p) 计算条件数。

• 如果输入矩阵是稀疏矩阵，cond 将忽略任何指定的 p 值并调用 condest。