【实验目的】
- 熟悉图数据结构的基本特征、构造方法
- 理解迪杰斯特拉算法、弗洛伊德算法寻找最小路径的原理
- 练习上述数据结构与算法的实现。
【实验原理】
- 图的创建与遍历算法
- 迪杰斯特拉算法从给定的一点出发,求该点到所有其他顶点的最短路径,我们将顶点集合G分成已经求出最短路径的点的集合She 尚未求出最短路径的点的集合(T=V-S)两部分,我们将T中的点按照距离递增的次序加到S中,并将最短距离记录到D中。
【实验内容】
-
问题描述:
创建一个至少有15个点的有向网表示的某个旅游景点的导游图。顶点代表景点,类型为字符串(例如,泰山导游图:“天地广场门”,“十八盘”,“冯玉祥墓”,“桃花峪门”,“中天门”,“南天门”,“玉皇顶”等),弧表示两个景点之间可以直达,弧上的权值表示两个景点之间的路程(公里数),弧上还有到达方法的信息(有步行和索道两种)。建立一个游客咨询系统。 -
基本要求 :
(1)创建图的存储结构;
(2)输入两个景点名,就可以得到从一个景点到达另一个景点的所有简单路径、相应路径的路程公里数、行走的方法(每一段是步行,还是坐索道);
(3)输入两个景点名,就可以得到其最短路径,即:路程最短的行进方法;如果两者无路径可通,就得出“两景点不可达的信息”。 -
重点、难点
重点:
(1)通过实验掌握图状结构数据的存储与表式;
(2)通过实验掌握对图的存储、遍历、运算等各种操作;
(3)深入理解图的特征及应用;
难点:
(1)任意两个景点所有路径的计算;
(2)最短路径的计算与算法设计。
【程序代码与运行结果】
BasicDefine.h
#pragma once
#include<stdlib.h>
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<string>
#define MAX 32767
#define INFINITY 32767
#define SPOTS_MAXNUM 30
using namespace std;typedef struct NUM
{int length;//路径长度int way;//表示通行方法
}Path;
typedef struct//旅游景点信息数据类型
{char name[30];//景点名int num;//景点编号
}Spot;typedef struct
{Spot spots[SPOTS_MAXNUM]; //旅游景点信息NUM pathMat[SPOTS_MAXNUM][SPOTS_MAXNUM]; //路径int vexnum, edgenum; //景点数目、路径数目
}Map;Map *CreateMap(Map *G); //创建地图
void Dijkstra(Map *G, int v0); //迪杰斯特拉算法寻找最短路径
int MatchNum(Map *G, char a[]); //根据景点名匹配其编号
void FindPath(Map *G, int i, int j, int k, int &a); //递归调用,寻找所有路线
void disppath(Map *G, int start, int end, int &a); //初始化相关数组,调用path函数
void ShowPath(int start, int end); //显示路径
void SearchAllpath(Map *G); //寻找所有路径
void SpotsList(Map *G); //显示所有景点
void Menu(); //用户界面
void Exit(); //退出界面interface.cpp
#include"BasicDefine.h"void SpotsList(Map *G)
{int i;cout << "〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓\n";cout << " 编号 景点名称 \n";for (i = 1; i <= G->vexnum; i++) {cout << " " << G->spots[i].num << " " << G->spots[i].name << endl;}cout << "〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓\n";
}void Menu()
{cout << endl;cout << "****\t1.查询任意两个景点间的最短路径\t****" << endl;cout << "****\t2.查询任意两个景点间的所有路径\t****" << endl;cout << "****\t3.退出系统 \t****" << endl;cout << "请选择:";
}void Exit()
{cout << " 〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓" << endl;cout << " □ □" << endl;cout << " □ 感谢您的使用! □" << endl;cout << " □ □" << endl;cout << " 〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓" << endl;
}main.cpp
#include"BasicDefine.h"Map *G;Map *CreateMap(Map *G) //创建地图
{int i, j, k, w, p;int max = 0;cout << "请输入旅游景点数目:";cin >> G->vexnum;for (i = 1; i < G->vexnum; i++) {max += i;}cout << "请输入路径数目";cout << "(注:路径数取值范围[" << G->vexnum - 1 << ", " << max << "]):" ;cin >> G->edgenum;cout << endl << "请依次输入景点的编号和名称,用空格隔开,如:1 安徽大学" << endl;for (i = 1; i <= G->vexnum; i++){cin >> G->spots[i].num >> G->spots[i].name;}cout << endl << "景点代号及名称输入完毕!" << endl;system("pause");system("cls");SpotsList(G);for (i = 1; i <= G->vexnum; i++)for (j = 1; j <= G->vexnum; j++)G->pathMat[i][j].length = INFINITY;//初始化邻接矩阵cout << "请依次输入两个景点的编号、它们的距离以及通行方式,用空格隔开" << endl;cout << "注意:距离单位为M,通行方式为0表示步行,1表示做索道" << endl;cout << "输入示例:1 4 9 0" << endl;for (k = 1; k <= G->edgenum; k++){cout << "第" << k << "条边:\t";cin >> i >> j >> w >> p;G->pathMat[i][j].length = w;G->pathMat[i][j].way = p;}return G;
}long int Dist[SPOTS_MAXNUM];
int p[SPOTS_MAXNUM][SPOTS_MAXNUM];void Dijkstra(Map *G, int v0) //迪杰斯特拉算法寻找最短路径
{int v, w, k, min, x, i;int path[SPOTS_MAXNUM];for (v = 1; v <= G->vexnum; v++){path[v] = 0;Dist[v] = G->pathMat[v0][v].length;//用Dist数组存储其路径for (w = 1; w <= G->vexnum; w++)p[v][w] = 0;if (Dist[v] < MAX){p[v][v0] = 1;p[v][v] = 1;}}Dist[v0] = 0; //vo到vo的路径长度为0path[v0] = 1; //vo到vo不用求路径for (i = 1; i <= G->vexnum; i++)//开始主循环。每次求得vo到某个顶点v的最短路径{min = INFINITY;for (w = 1; w <= G->vexnum; w++)if (!path[w])if (Dist[w] < min){v = w;min = Dist[w];}path[v] = 1;for (w = 1; w <= G->vexnum; w++)if (!path[w] && (min + G->pathMat[v][w].length < Dist[w])){Dist[w] = min + G->pathMat[v][w].length;for (x = 1; x <= G->vexnum; x++)p[w][x] = p[v][x];p[w][w] = 1;}}
}
int MatchNum(Map *G, char a[]) //根据景点名匹配其编号
{int i;for (i = 1; i <= G->vexnum; i++)if (strcmp(G->spots[i].name, a) == 0)break;if (i == (G->vexnum + 1))return -1;elsereturn G->spots[i].num;
}int visited[SPOTS_MAXNUM];
int v[SPOTS_MAXNUM];
void FindPath(Map *G, int i, int j, int k, int &a) //递归调用,寻找所有路线
{int s;if (v[k] == j){a++;cout << "第" << a << "条:";string ways;for (s = 1; s < k; s++) {ways = (G->pathMat[v[s]][v[s + 1]].way == 0) ? "步行" : "索道";cout << G->spots[v[s]].name << "-("<<G->pathMat[v[s]][v[s + 1]].length <<"m"<< ways << ")->";}cout << G->spots[v[s]].name << endl;}s = 1;while (s <= G->vexnum){if (s != i){if (G->pathMat[v[k]][s].length != MAX && visited[s] == 0){visited[s] = 1;v[k + 1] = s;FindPath(G, i, j, k + 1, a);visited[s] = 0;}}s++;}
}
void disppath(Map *G, int start, int end, int &a) //初始化visit数组,调用path函数
{ int k;v[1] = start;for (k = 1; k <= G->vexnum; k++)visited[start] = 0;FindPath(G, start, end, 1, a);
}void SearchAllpath(Map *G)
{//输入起点与终点,调用disppath函数寻找路径 int i, j; //i代表起点,j代表终点 char b[10], c[10];cout << "请输入起点景点名称:";cin >> b;i = MatchNum(G, b);getchar();if (i == -1){cout << "您输入的起点景点不存在!" << endl;return;}cout << "请输入终点景点名称:";cin >> c;j = MatchNum(G, c);getchar();if (j == -1){cout << "您输入的终点景点不存在!" << endl;return;}int a = 0;disppath(G, i, j, a);if (a == 0) {cout << "两景点不可达!" << endl;}else {cout << "共" << a << "条路径!" << endl;}
}void ShowPath(int start, int end) //显示路径
{int a, b, c, d, q = 0;a = end;if (a == start)cout << "起点与终点相同!" << endl;else if (Dist[a] >= INFINITY)cout << "两景点不可达!" << endl;else{cout << "\n从" << G->spots[start].name << "到" << G->spots[end].name << "的最短路径是";cout << "\t" << G->spots[start].name;d = start;for (c = 1; c <= SPOTS_MAXNUM; c++){here:p[a][start] = 0;string ways;for (b = 1; b <= SPOTS_MAXNUM; b++){if (G->pathMat[d][b].length < MAX&&p[a][b]){ways = (G->pathMat[d][b].way == 0) ? "步行" : "索道";cout << "--(" << G->pathMat[d][b].length << "m" << ways << ")-->" << G->spots[b].name;p[a][b] = 0;d = b;goto here;}}}cout << endl << "距离为" << Dist[a] << "m\n\n\t";}
}int main(void)
{int i;int v0, v1;G = (Map *)malloc(sizeof(Map)); //初始化变量G = CreateMap(G); //创建地图system("cls");Menu(); //显示交互界面cin >> i;while (1){switch (i){case 1: //查询任意两个景点间的最短路径system("cls");SpotsList(G);cout << "\n\n请选择起点景点:" ;cin >> v0;cout << "请选择终点景点:" ;cin >> v1;Dijkstra(G, v0);ShowPath(v0, v1);cout << "\n" << endl;system("pause"); system("cls");Menu();break;case 2: //查询任意两个景点间的所有路径system("cls");SpotsList(G);SearchAllpath(G);system("pause"); system("cls");SpotsList(G);Menu();break;case 3: //退出system("cls");Exit();return 0;default:cout << "请重新选择:" << endl;break;}cin >> i;}
}输入的景点信息为:
- 文典阁
- 博学北楼
- 博学南楼
- 笃行北楼
- 笃行南楼
- 行知楼
- 适之楼
- 艺术楼
- 体育馆
- 鸣磬广场
- 教学主楼
- 逸夫楼
- 问津楼
- 电化楼
- 眼镜湖
输入的路径信息为:
1 2 300 0
1 3 300 0
1 4 200 0
1 5 200 0
1 6 600 0
1 7 800 1
1 8 1200 1
1 9 1300 1
1 10 200 0
2 4 50 0
2 6 100 0
3 5 100 0
3 7 600 0
4 10 500 0
5 9 1600 1
5 10 600 0
6 8 400 0
6 9 1100 1
7 8 600 0
8 9 1400 1
10 12 9000 1
11 12 400 0
11 13 300 0
11 14 400 0
11 15 500 0
12 13 700 0
12 14 600 1
13 14 900 1
13 15 500 1
14 15 200 0
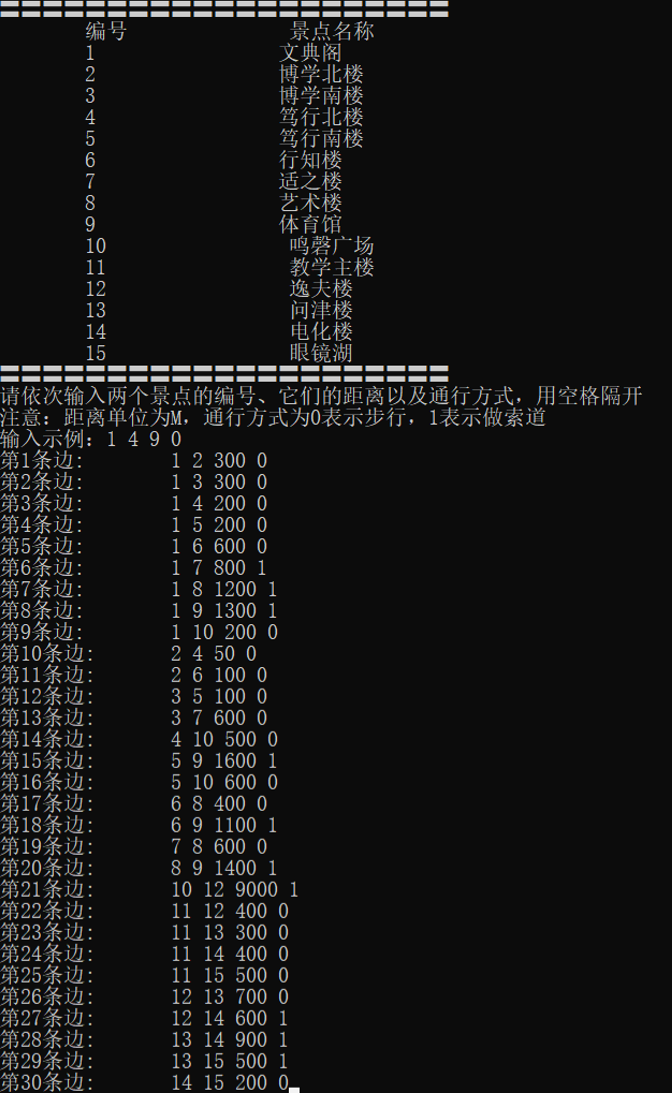
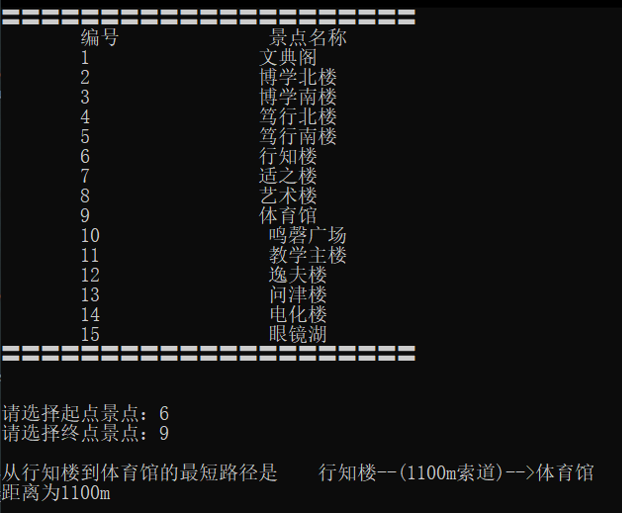
查询最短路径

从 行知楼 到 体育馆:
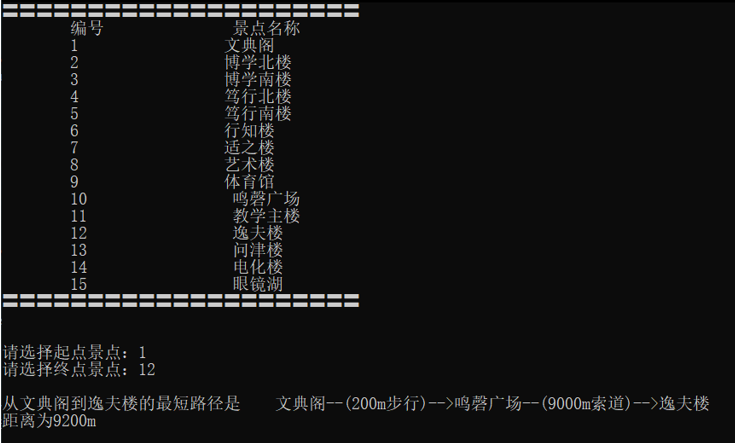
从 文典阁 到 逸夫楼
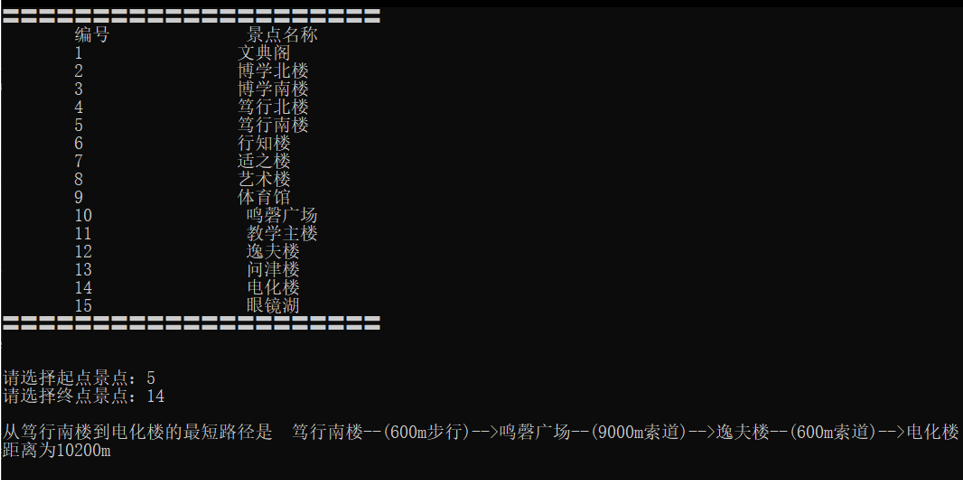
从 笃行南楼 到 电化楼
查询所有路径
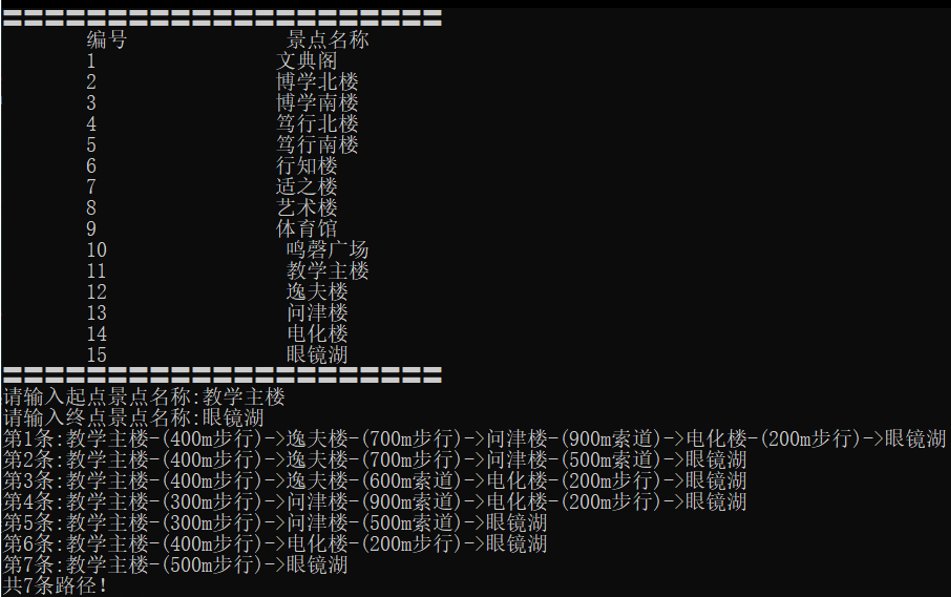
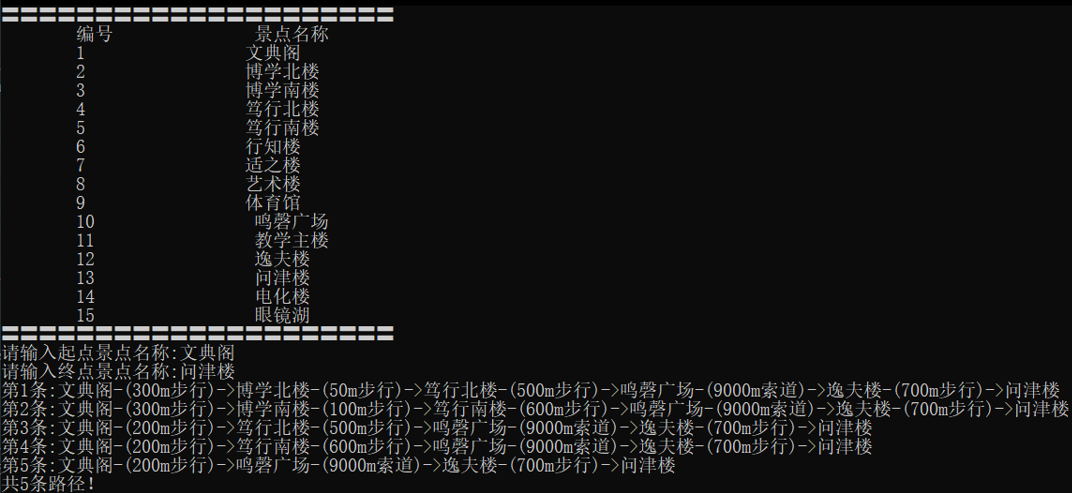
从 文典阁 到 问津楼
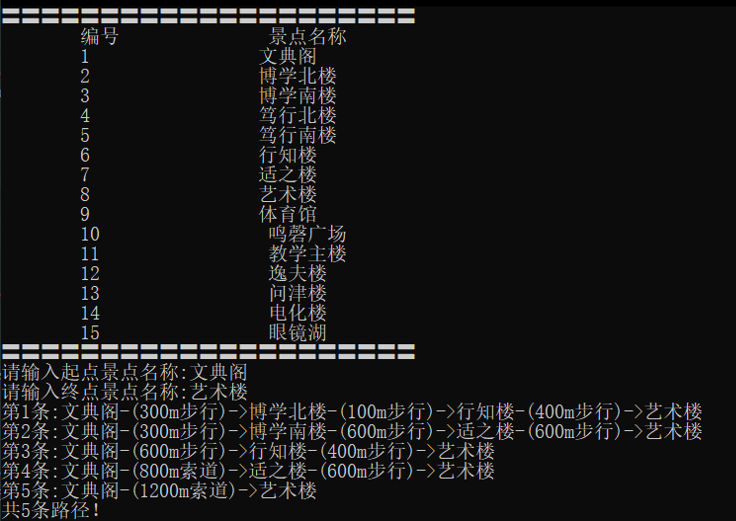
从 文典阁 到 艺术楼
从 教学主楼 到 眼镜湖