跟李沐学AI：循环神经网络RNN

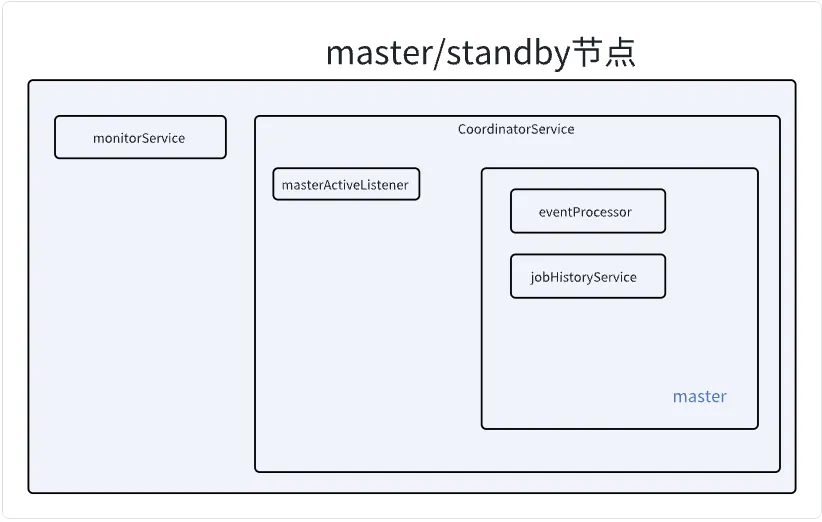
循环神经网络

循环神经网络（recurrent neural networks，RNNs）是具有隐状态的神经网络。RNN 具有隐状态（hidden state）的原因在于它需要一种机制来存储之前输入的信息，以便于处理当前输入时能够考虑之前的上下文。基于上节提到的潜变量自回归模型： $p(x_t\mid x_{t-1},\dots ,x_1)\approx p(x_t | h_{t-1})$ 。其中 $h_{t-1}$ 是隐状态（hidden state），也称为隐藏变量（hidden variable），它存储了到时间步t−1的序列信息。通常，我们可以基于当前输入 $x_t$ 和先前隐状态 $h_{t-1}$ 来计算时间步t处的任何时间的隐状态： $h_t=f(x_t,h_{t-1})$ 。在每一个时间步t，RNN 接收一个输入xt以及来自上一时间步的隐状态ht−1，并根据这两个信息计算出当前时间步的隐状态ht。隐状态可以看作网络对于之前所有输入的记忆表示，它包含了从序列开始到当前时间步所有信息的摘要。

循环神经网络的输出 $o_t$ 由 $h_t$ 决定， $h_t=f(W_{xh}x_t + W_{hh}h_{t-1}+b)$ 。

其中：ht是当前时间步t的隐状态，xt是当前时间步的输入，Wxh和Whh分别是从输入到隐状态和从隐状态到隐状态的权重矩阵，b是偏置项，f(⋅)是激活函数，例如tanh或ReLU等。

困惑度

困惑度（Perplexity, PP）用来衡量模型预测单词的能力，它反映了模型对未知数据的“困惑”程度。通常情况下，困惑度越低，说明模型对数据的拟合程度越好。困惑度计算公式如下：

在最好的情况下，模型总是完美地估计标签词元的概率为1。在这种情况下，模型的困惑度为1。

在最坏的情况下，模型总是预测标签词元的概率为0。在这种情况下，困惑度是正无穷大。

梯度裁剪

在循环神经网络（RNNs）中，梯度裁剪是一种常用于缓解梯度消失或梯度爆炸问题的技术。

在RNN中，梯度消失的问题尤为显著，因为它们的权重需要通过时间进行反向传播。在每一时间步中，梯度是通过链式法则计算的，这意味着当前时间步的梯度是由前一时间步的梯度乘以前一时间步的权重矩阵得到的。如果这个权重矩阵的特征值小于1，那么经过多次相乘之后，梯度就会逐渐减小至接近零。当这种情况发生时，网络就很难调整其权重来学习远距离的时间依赖性。这就是梯度消失。与梯度消失相反，梯度爆炸发生在梯度增长得非常快以至于变得过大，这可能导致权重参数的剧烈更新，使得模型难以收敛。

梯度裁剪的目的是通过限制梯度的大小来解决这些问题。具体来说，当计算出的梯度超过某个预定义的阈值时，可以按比例缩小梯度的值，使得它们不会过于庞大，从而避免梯度爆炸。这个过程可以通过两种常见的方式来实现：