Transformers 中的 Softmax 可以并行加速么?
面试题
Softmax 如何并行?
Softmax 计算公式
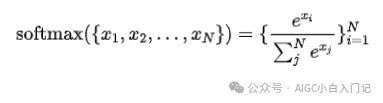
安全的 Softmax 运算
Softmax函数在深度学习中广泛应用于多分类问题的输出层,它通过指数化和归一化将一个实数向量转换为概率分布。然而,在实际计算中,Softmax函数可能会遇到数值溢出的问题,尤其是当输入值较大或者采用半精度(如FP16)进行计算时。
数值溢出分为上溢出和下溢出。上溢出发生在指数函数的参数非常大时,导致计算结果超过了浮点数的最大表示范围,结果可能变为无穷大(Inf)。下溢出则是指数函数的参数非常小,导致计算结果趋近于0,可能会被计算机舍入为0,这在Softmax函数的分母中尤其成问题,因为分母接近于0会导致最终结果不稳定。
为了解决这个问题,通常采用的一种方法是从每个输入值中减去向量中的最大值,即进行数值稳定化处理。这种方法可以减少指数函数的参数范围,从而避免上溢出。具体来说,对于输入向量 ,Softmax函数的计算公式可以修改为:
$\text{softmax}(x_i) = \frac{e^{x_i - \max(x)}}{\sum_{j=1}^{n} e^{x_j - \max(x)}}
$其中,是输入向量中的最大值。这样,减去最大值后,最大的指数参数不会超过0,从而避免了上溢出。同时,由于分母中至少有一项是1(当 是最大值时),这也避免了下溢出的问题。
此外,还可以使用LogSoftmax来进一步增强数值稳定性。LogSoftmax首先计算Softmax,然后取对数,这样可以将上溢出和下溢出的风险降到最低。
在实际应用中,深度学习框架如PyTorch和TensorFlow等,已经内置了数值稳定化的Softmax实现,可以直接使用而无需手动进行数值稳定化处理。例如,PyTorch中的nn.Softmax和nn.LogSoftmax模块就已经考虑了数值稳定性问题。
具体来说,可以采用以下方式来保证计算 softmax 时的数值稳定性
- step 1: 计算 x 的最大值 m
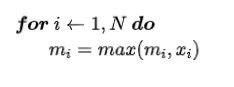
- step 2: 计算 softmax 分母
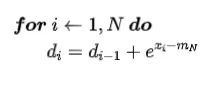
- step 3: 计算对应位置的 softmax
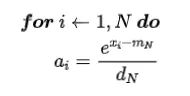
由此可见,若不采取任何优化措施,至少需要与GPU进行6次数据交换(包括3次数据写入和3次读取)。
如果我们对循环的每一步实施并行分割,还需额外承担如 reduce_sum 和 reduce_max 操作的通信开销。
我们能否通过整合某些操作来减少通信次数?根据以往在layernorm并行化中的实践经验,我们需要开发一种在线算法来实现这一目标。
Online Softmax
在 2018年 Maxim Milakov和Natalia Gimelshein 发表《Online normalizer calculation for softmax》,文章提出了一种称为“Online Softmax”的算法,该算法能够在单次遍历输入向量的过程中同时计算最大值和归一化项,从而将每个向量元素的内存访问次数从4次减少到3次。这种方法的灵感来自于数值稳定的方差计算在线算法。文章还提出了一种并行版本的在线归一化计算方法,以及一种将Softmax和TopK操作融合的方法,进一步提高了性能。
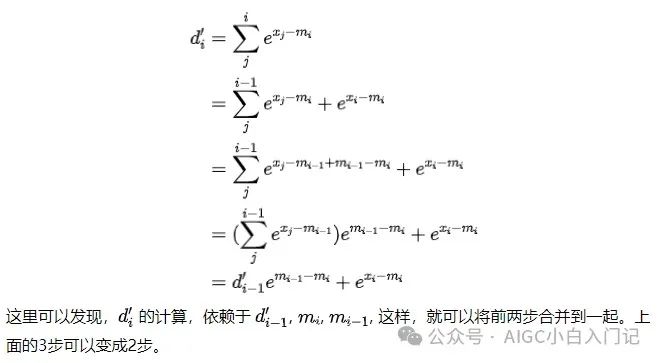
我们再来看一下第二步:
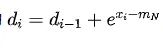
可以看出,如果能够去掉这个式子对 的依赖,那么就能对 softmax 进行并行加速。
假设
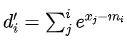
注:这里减去的全局最大值变成了当前最大值。这个式子有如下的性质
- 求解 x 的最大值 m, 和计算 softmax 的分母
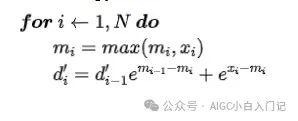
- 求对应位置的 softmax

我们是否能够进一步整合操作?似乎已经达到极限了,因为第二步的计算结果依赖于第一步的输出。
不过,我们可以利用GPU的共享内存来暂存中间数据,通过一个单一的kernel执行上述两个步骤,这样就可以减少与全局内存的交互次数,仅需进行一次数据写入和一次结果读取。
总结
总体而言,优化的关键在于两个主要策略:
- 通过融合前两个计算步骤,降低执行Reduce_max和Reduce_sum等操作的通信开销。
- 利用共享内存来存储临时数据,以减少对全局内存的访问成本。