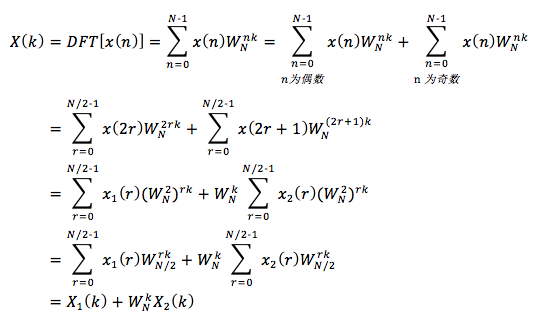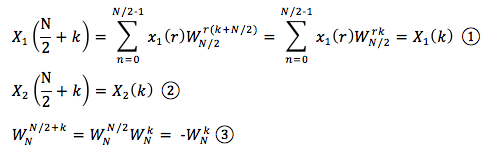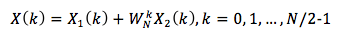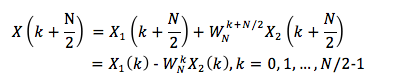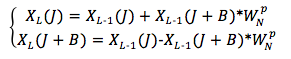FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。采样频率要大于信号频率的两倍。为了方便进行FFT运算,通常N取2的整数次方。
一、DFT
1.1 原理
定义(来自百科):离散傅里叶变换(Discrete Fourier Transform,缩写为DFT),是傅里叶变换在时域和频域上都呈离散的形式,将信号的时域采样变换为其DTFT的频域采样。在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT,也应当将其看作其周期延拓的变换。在实际应用中通常采用快速傅里叶变换计算DFT。
DFT的公式是:设x(n)为M点的有限长序列,即在0≤n≤M-1内有值,则定义x(n)的N点(N≥M。当N>M时,补N-M个零值点),离散傅里叶变化定义为

其中,为旋转因子(为方便编辑后续记作W(N, nk),特此说明),其计算公式为
,具有以下性质:
①周期性:W(N, nk) = W(N, (n+rN)k) = W(N, n(k+rN)),其中r问整数。
②共轭对称性:(W(N, nk))* = W(N, -nk)。
③可约性:W(N, nk) = W(mN, mnk),W(N, nk) = W(N/m, nk/m),其中m为整数,N/m为整数。
④特殊值:W(N, N/2) = -1; W(N, (k+N/2)) = -W(N, k);
W(N, (N-k)n) = W(N, (N-n)k) = W(N, -nk)。
所以,在计算旋转因子的过程中可以适当的使用特殊值来提高运算的效率。
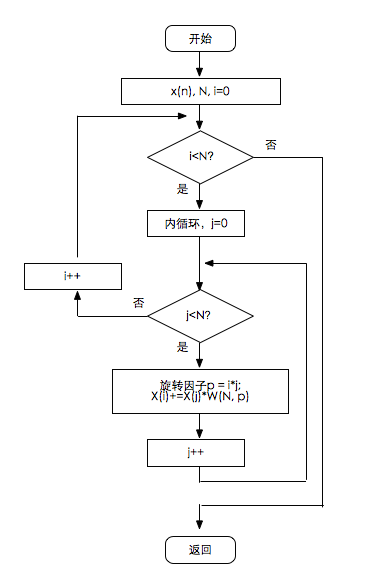
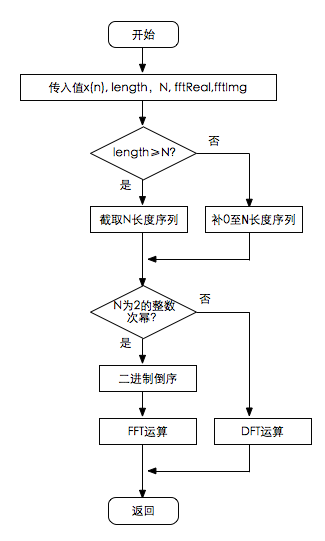
在计算DFT时,如果数据的点数够计算的点数,则截取计算点数长的数据进行DFT运算,否则将数据点个数补0至计算点个数,然后进行计算,举例如下(举例只是为了说明问题,没有按照编程语言的书写格式)。
比如:数据点数组为 dataArray = {1, 2, 3, 4,5},可以看出数据长度为5。
如果要求做4点DFT运算,则只需截取前4个数作为运算数组进行运算即可,即为{1, 2, 3, 4};
如果要求做8点DFT运算,则需在原数组后补三个0,使长度为8后再进行计算,计算数组为{1, 2, 3, 4,5,0,0,0}。
1.2 流程图
二、FFT
2.1 原理
设序列x(n)点数为N=2^L,L为整数。将N=2^L,先按照n的奇偶分为两组,
其中r = 0, 1, ..., N/2-1,x(2r) = x1(r),x(2r-1) = x2(r);
则可将DFT化为
由上式可以看出一个N点的DFT可以分为两个N/2点的DFT,按照上式右组合成N点DFT。但是这里的x1(r)、x2(r)以及X1(k)、X2(k)都是N/2点的序列,即r,k满足r,k=0, 1, ..., N/2-1。而X(k)却有N点,上式计算的只是X(k)的前半项数的结果,因此还需要计算后半项的值。
将①②③代入(式1),就可将X(k)表达为前后两部分:
前半部分,X(k),当k=0, 1, ..., N/2-1
后半部分,X(k),当k=N/2, ..., N-1
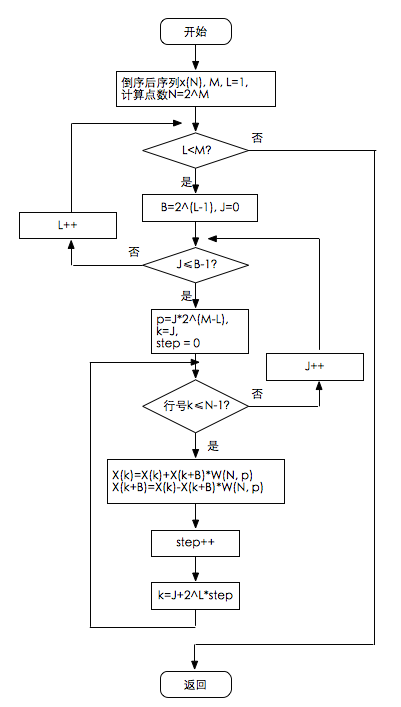
2.2 流程图
①FFT运算总流程图,包括
②根据(1)中推导的内容,FFT的流程图可化为
蝶形运算中又三层循环
第一层(最外层),完成M次迭代过程,即算出A0(k), A1(k), ..., Am(k),其中k=0, 1, ..., N;A2(k)为蝶形运算第2级的结果,如A0(k)=x(k), Am(k)=X(k);
第二层(中间层),完成旋转因子的变化,步进为2^L;
第三层(最里层),完成相同旋转因子的蝶形运算。
三、DFT与FFT
1.DFT的运算量
复数乘法次数为N*N,复数加法次数为N(N-1),若N>>1,则这两者都近似为N*N,它随N增大为急速增大。改进途径:①利用旋转因子性质减小计算量;②由于运算量和N*N成正比,因而可将N点DFT分解成小点数的DFT,以减少运算量(点数越小,计算量越小);③改为用FFT计算,复数乘法次数为(N/2)*log(2,N)。
2.FFT可分为按照时间抽选的基-2算法(库利-图基算法DIT-FFT)和按频率抽选的基-2算法(桑德-图基算法DIF-FFT)。
3.FFT计算原理
FFT的计算要求点数必须为2的整数次幂,如果点数不够用0补齐。例如计算{2,3,5,8,4}的8点FFT,需要补3个0后进行计算,如果计算该数组的5点FFT,则先计算8点FFT后截取前5个值即可(不提倡)。
四、蝴蝶运算
4.1 基本流程
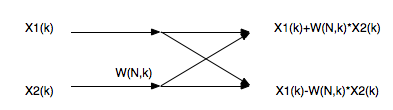
蝶形运算,符号表示如下图所示:
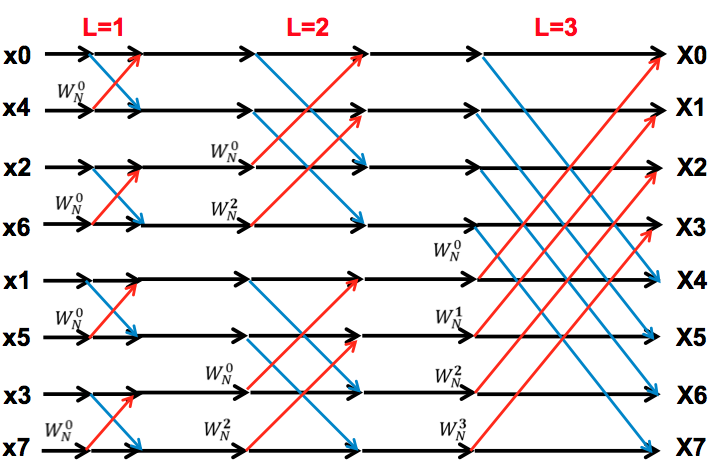
所以,FFT的蝶形运算图表示为(8点,2^3 = 8,运算级数最大为L=3)
在蝶形运算中变化规律由W(N, p)推导,其中N为FFT计算点数,J为下角标的值
L = 1时,W(N, p) = W(N, J) = W(2^L, J),其中J = 0;
L = 2时,W(N, p) = W(N, J) = W(2^L, J),其中J = 0, 1;
L = 3时,W(N, p) = W(N, J) = W(2^L, J),其中J = 0, 1, 2, 3;
所以,W(N, p) = W(2^L, J),其中J = 0, 1, ..., 2^(L-1)-1
又因为2^L = 2^M*2^(L-M) = N*2^(L-M),这里N为2的整数次幂,即N=2^M,
W(N, p) = W(2^L, J) = W(N*2^(L-M), J) = W(N, J*2^(M-L))
所以,p = J*2^(M-L),此处J = 0, 1, ..., 2^(L-1)-1,当J遍历结束但计算点数不够N时,J=J+2^L,后继续遍历,直到计算点数为N时不再循环。
4.2 举例:N=8点的FFT计算
当L=2时,J = 0, 1两个值,因此p = J*2^(M-L) = 0, 2两个值,即旋转因子有两个值W(8, 0)和W(8, 2),计算中两行之间的距离B = 2^(L-1)=2^(2-1)=2,
代入J=0, 1可求得X(0)、X(0+2)和X(1)、X(1+2),即可求出第2级蝶形运算的X(0), X(1), X(2), X(3),也就是求出一半,此时J加步进2^L=4,即J=J+2^L=4, 5,
再代入J=4, 5可求出X(4), X(4+2)和X(5), X(5+2),即可求出第2级蝶形运算的X(4), X(5), X(6), X(7),已经全部求出,J循环结束。
4.3 二进制倒序说明
前面数的排列顺序是进行二进制倒序后的排序。二进制倒序是指将某数转化为二进制表示,将最高位看做最低位、次高位看做次低位...以此类推,计算后的纸进行排序。例如3的二进制表示为011b(3=0*2^2+1*2+1),二进制倒序值为6(011b,最高位看做最低位...即6=0+1*2+1*2^2)
即0到7的二进制排序是:
0, 4, 2, 6, 1, 5, 3, 7
000→000 001→100 010→010 011→110 100→001 101→101 110→011 111→111
五、从振幅或快速傅立叶变换到dB
从振幅或快速傅立叶变换到dB是一个涉及信号处理和单位转换的问题。
函数f(t)为一元连续函数,其傅里叶变换定义为:

其中,i为虚数单位。欧拉公式:
![]()

5.1 相关名词
1.振幅(Amplitude):振幅是指信号的最大偏离值,表示信号的强度或能量大小。在信号处理中,振幅常用于描述波形的高低或振动的幅度。
2.dB(分贝):分贝是一种用于表示信号强度或功率比例的对数单位。在信号处理中,分贝常用于描述信号的增益或衰减程度。分贝的计算公式为:dB = 10 * log10(P1/P0),其中P1为信号的功率,P0为参考功率。当保持输入信号的幅度不变,改变频率使输出信号降至最大值的0.707倍,即用频响特性来表述即为-3dB点处即为截止频率,它是用来说明频率特性指标的一个特殊频率。
利用系统函数的模来表示电路的放大倍数,由于20lgA(ω)=-3dB,解得
A(ω)=10^-0.15=0.707945784≈1/√2,又因为A(ω)=|H(jω)|,则|H(jω)|^2=1/2
在高频端和低频端各有一个截止频率,分别称为上截止频率和下截止频率。两个截止频率之间的频率范围称为通频带。
5.2 物理意义理解
假设采样频率为Fs,信号频率F,采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。
1.幅值:这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍。
2.相位:而每个点的相位呢,就是在该频率下的信号的相位。
3.分辨率:第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。例如某点n所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
4.表达式:假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=根号a*a+b*b,相位就是Pn=atan2(b,a)。根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn*t+Pn),即2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号,是直流分量,幅度即为A1/N。
由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
5.3 示例
假设我们有一个信号,它含有2V的直流分量,频率为50Hz、相位为-30度、幅度为3V的交流信号,以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下(式中cos参数为弧度,所以-30度和90度要分别换算成弧度):
S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)
我们以256Hz的采样率对这个信号进行采样,总共采样256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第50个点、第76个点上出现峰值,其它各点应该接近0。
| 幅值 | 相位(弧度) | 相位(角度) | |
| 直流分量 | 512/N =512/256 =2 | \ | \ |
| 50Hz | 384/(N/2) =384/(256/2) =3 | atan2(-192, 332.55) =-0.5236 | (-0.5236)/pi =-30.0001 |
| 75Hz | 192/(N/2) =192/(256/2) =1.5 | atan2(192, 3.4315E-12) =1.5708 | 180*1.5708/pi =90.0002 |

(图片横坐标为第几个点,即Hz;纵坐标为模)
5.4 波特图
1、伯德图的定义
伯德图由对数幅频特性和对数相频特性两条曲线构成。 伯德图一般是由二张图组合而成, 伯德图由两张图组成:①G(jω)的幅值(以分贝,dB表示)-频率(以对数标度)对数坐标图,其上画有对数幅频曲线;②G(jω)的相角-频率(以对数标度)对数坐标图,其上画有相频曲线。
对数幅值的标准表达式为20 lg|G(jω)|,单位是分贝,相角的单位是度。由于增益用对数来表示(log(ab)=log(a)+log(b)),因此一传递函数乘以一常数,在伯德增益图只需将图形的纵向移动即可,二传递函数的相乘,在波德幅频图就变成图形的相加。幅频图纵轴0分贝以下具有正增益裕度、属稳定区,反之属不稳定区。
配合波德相频图可以估算一信号进入系统后,输出信号及原始信号的比例关系及相位。例如一个Asin(ωt) 的信号进入系统后振幅变原来的k倍,相位落后原信号Φ,则其输出信号则为(Ak)sin(ωt−Φ),其中的k和Φ都是频率的函数。相频图纵轴-180度以上具有正相位裕度、属稳定区,反之属不稳定区。
2、伯德图的画法
画伯德图时,分三个频段进行,先画幅频特性,顺序是中频段、低频段和高频段。将三个频段的频率特性(或称频率响应)合起来就是全频段的幅频特性,然后再根据幅频特性画出相应的相频特性来。 作伯德图时,首先写出频率特性,然后按常数因子K、积分和微分因子(jω)、一阶因子(1+jωT)和二阶因子[1+2ζ(jω/ωn)+(jω)/ω]1这样四种基本因子分别画出伯德图,再总加而成。
下图是常见简易传递函数的伯德图趋势:

五、代码实现(C语言)
FFT.H

FFT.C








六、代码实现(Matlab)
基于MATLAB/Simulink的2ASK数字带通传输系统建模与仿真
相关文章
十分简明易懂的FFT(快速傅里叶变换)
彻底搞懂快速傅里叶变换FFT核心思想--分而治之
数字信号处理公式变程序(一)——DFT、FFT
实验笔记【3】| 利用matlab进行fft分析
信号处理之快速傅里叶变换(FFT)-通俗易懂
深入浅出的理解频谱泄露
快速傅里叶变换(FFT)和小波分析在信号处理上的应用