文章目录
- 题目链接:
- 题目描述:
- 解法
- C++ 算法代码:
- 图解
题目链接:
209. 长度最小的子数组
题目描述:

解法
解法一:暴力求解(会超时)
暴力枚举出所有子数组的和。
查找子数组n2,求和n
一共O(n3)
优化:
求和的时候,可以把上次求和的结果存起来,往后加一位的时候直接把那一位的值加到上次的和里面。
解法二:滑动窗口O(n)
利用
单调性,使用同向双指针来优化。(同向双指针也叫滑动窗口)
left=0,right=0,标记窗口的左右端点- 进窗口
- 判断,更新结果🌟,出窗口
2-3步是一直循环的
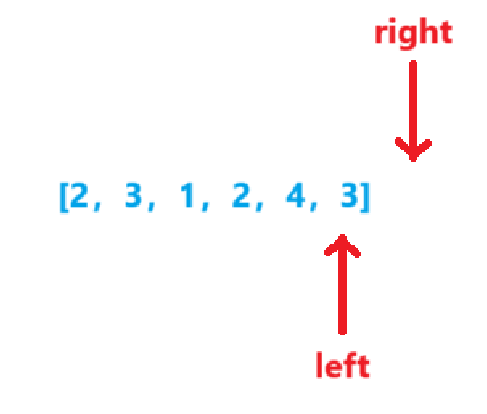
例如:nums=[2,3,1,2,4,3]

移动到sum>=target
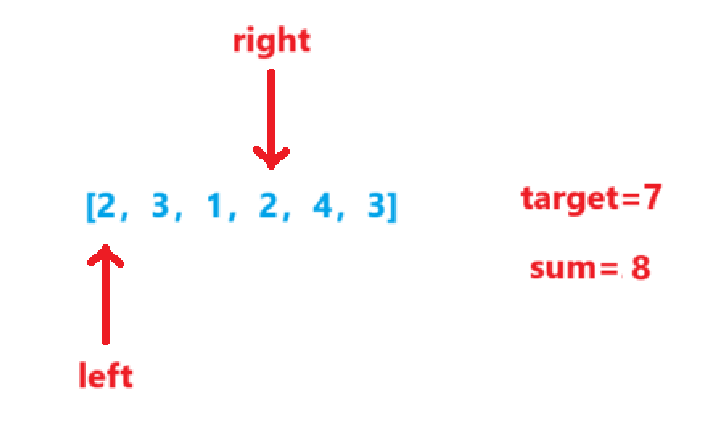
然后left右移,因为如果left不动,right继续往后得到的都不是长度最小的数组了。
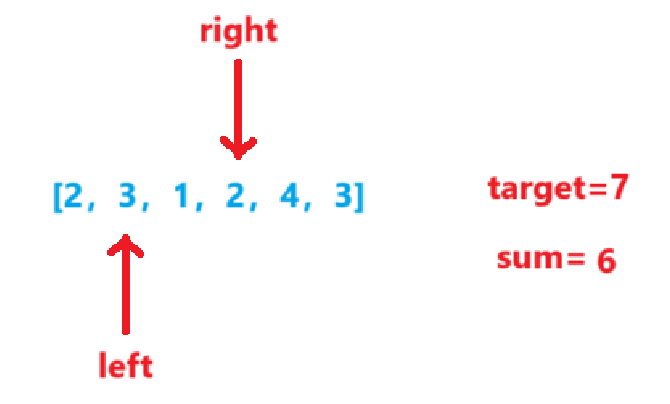
sum<target,right右移
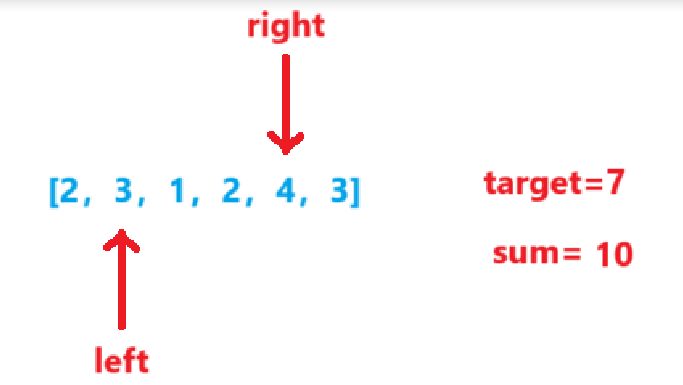
依次类推
然后窗口的长度可以用len来记录,每次判断后先更新结果,然后出窗口。
C++ 算法代码:
解法一:暴力求解(会超时)
class Solution {public:int minSubArrayLen(int target, vector<int>& nums) {// 记录结果int ret = INT_MAX;int n = nums.size();// 枚举出所有满足和大于等于 target 的子数组[start, end// 由于是取到最小,因此枚举的过程中要尽量让数组的长度最小// 枚举开始位置for (int start = 0; start < n; start++){int sum = 0; // 记录从这个位置开始的连续数组的和// 寻找结束位置for (int end = start; end < n; end++){sum += nums[end]; // 将当前位置加上if (sum >= target) // 当这段区间内的和满足条件时{// 更新结果,start 开头的最短区间已经找到ret = min(ret, end - start + 1);break;}}}// 返回最后结果return ret == INT_MAX ? 0 : ret;}
};
解法二:
class Solution
{public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size(), sum = 0, len = INT_MAX;for(int left = 0, right = 0; right < n; right++){sum += nums[right]; // 进窗口while(sum >= target) // 判断{len = min(len, right - left + 1); // 更新结果sum -= nums[left++]; // 出窗口}}return len == INT_MAX ? 0 : len;}
};
图解
nums=[2,3,1,2,4,3]
target=7
n=6,sum=0,right=0,left=0,target=7,len=INT_MAX(确保min使用的时候不会把len的初始值当作最小值)
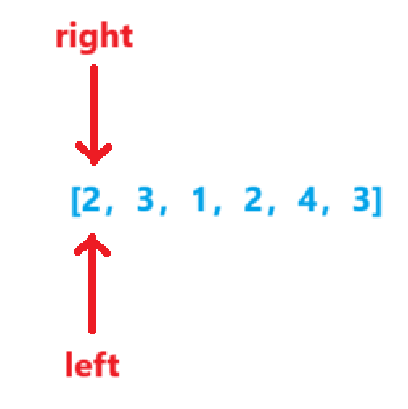
-
sum=2sum<target,right++
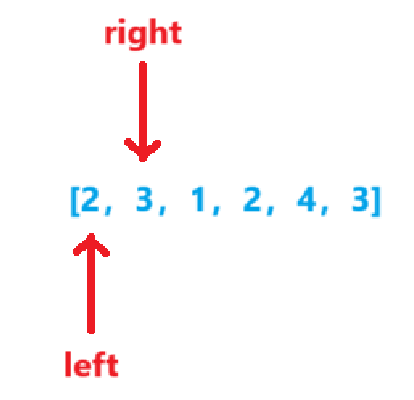
-
sum=5sum<target,right++
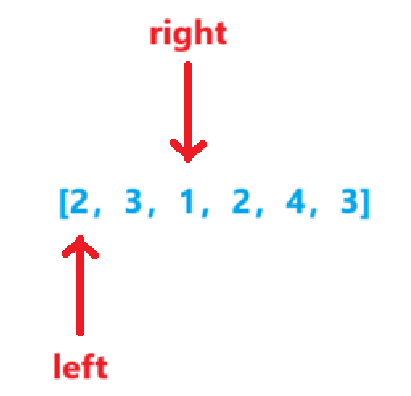
-
sum=5sum<target,right++
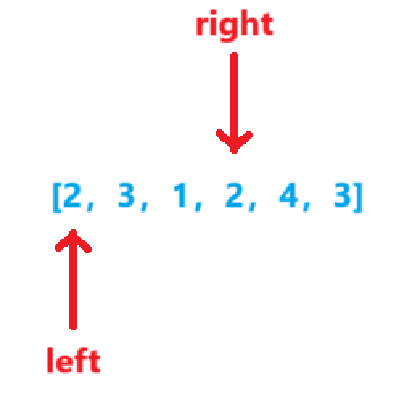
-
sum=8sum>target,len=4sum=sum-nums[left++]=8-2=6
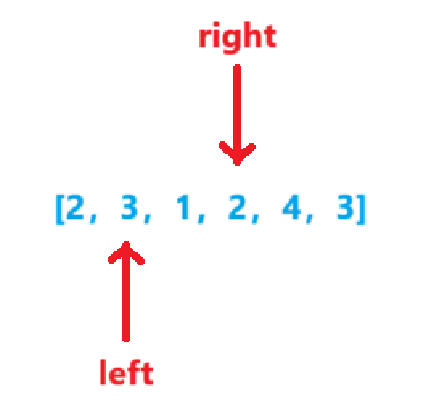
-
sum=6sum<target,right++
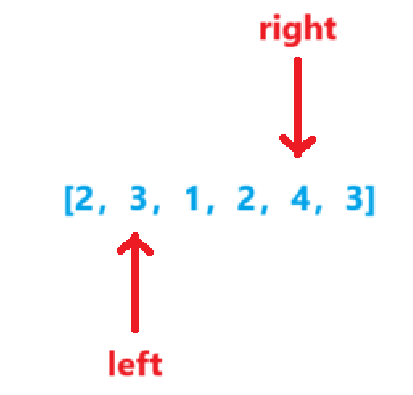
-
sum=10sum>target,len=4sum=sum-nums[left++]=10-3=7
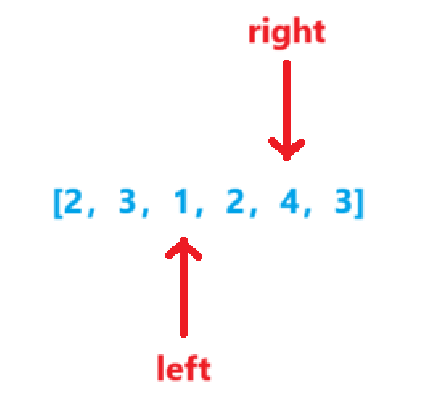
-
sum=7sum=target,len=3sum=sum-nums[left++]=7-1=6
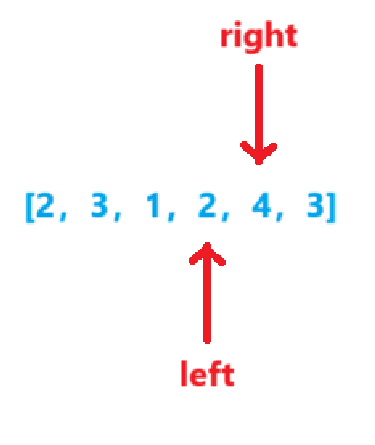
-
sum=6sum<target,right++
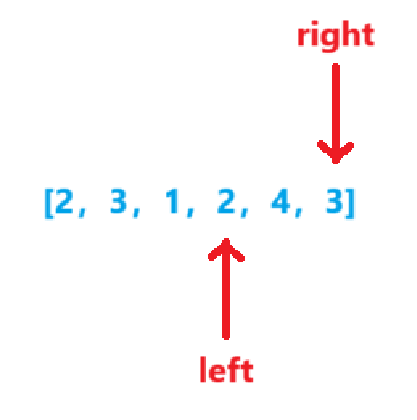
-
sum=9sum>target,len=3sum=sum-nums[left++]=9-2=7
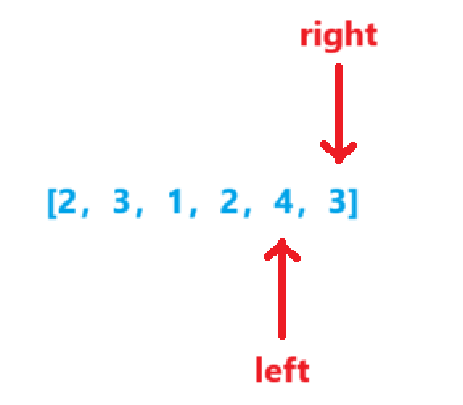
-
sum=7sum=target,len=2sum=sum-nums[left++]=7-4=3
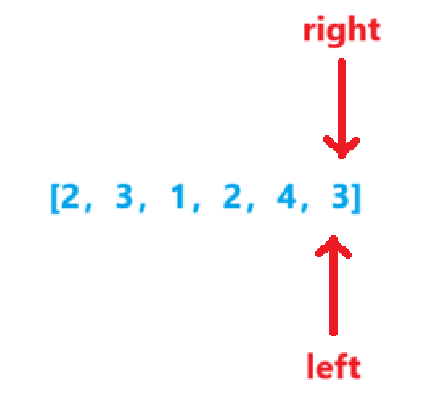
-
sum=3sum<target,right++
-
跳出
for循环,return len == INT_MAX ? 0 : len;,这里返回2 -
程序结束