目录
前言
一、什么是程函方程?
二、配置环境及库的导入
三、构建训练数据集
四、用Pytorch搭建PINN网络
1.网络搭建
2.一些基本参数变量的确定以及数据格式的转换
五、用Pytorch搭建PINN网络
六、查看loss下降情况
七、导入网络模型,输入验证数据,预测结果
八、对比画图
1、画出预测走时场
2、画出真实走时场
总结
前言
程函方程在地球物理学中对于走时场正演和射线追踪等具有很重要的意义。本文将简单介绍如何利用PINN解程函方程。
一、什么是程函方程?
程函方程是地球物理学中描述变速介质中时间场分布的基本方程,也是射线追踪方法的基础。在二维变速介质中的程函方程可以表示为如下的形式:
其中,为二维介质中的时间场分布,
为慢度分布。对于任意速度模型,给定任意一个炮点位置P,可以应用程函方程计算出对应的走时场,为射线追踪提供基础。
二、配置环境及库的导入
需要安装一些深度学习最基本的库以及pytorch。
import torch#深度学习的pytoch平台
import torch.nn as nn
from torch.autograd import Variable
import numpy as np
import random
import time#可以用来简单地记录时间
import matplotlib.pyplot as plt#画图
from mpl_toolkits.axes_grid1 import make_axes_locatable
#随机种子
random.seed(1234)
np.random.seed(1234)
torch.manual_seed(1234)
torch.cuda.manual_seed(1234)
torch.cuda.manual_seed_all(1234)
三、构建训练数据集
需要安装一些深度学习最基本的库以及pytorch。
# Number of training points
num_tr_pts = 10201
#prepare data
zmin = 0.; zmax = 2.; deltaz = 0.02;
xmin = 0.; xmax = 2.; deltax = 0.02;
# Point-source location
sz = 0.04; sx = 0.04;
z_sz = np.arange((num_tr_pts+1),dtype = np.float)
x_sx = np.arange((num_tr_pts+1),dtype = np.float)
for i in range(num_tr_pts+1):z_sz[i] = szx_sx[i] = sx
# random x and z point
z = np.arange(zmin,zmax+deltaz,deltaz)
nz = z.size
x = np.arange(xmin,xmax+deltax,deltax)
nx = x.size
Z,X = np.meshgrid(z,x,indexing='ij')
X_star = [Z.reshape(-1,1), X.reshape(-1,1)] # Grid points for prediction
selected_pts = np.random.choice(np.arange(0,Z.size),num_tr_pts,replace=False)
#selected_pts = np.arange(num_tr_pts)
Zf = Z.reshape(-1,1)[selected_pts]
Zf = np.append(Zf,sz)
Xf = X.reshape(-1,1)[selected_pts]
Xf = np.append(Xf,sx)
X_starf = [Zf.reshape(-1,1), Xf.reshape(-1,1)] # Grid points for training
# input data of all the points of model x z and xs zs
x_train = np.hstack((Zf.reshape(-1,1),Xf.reshape(-1,1),z_sz.reshape(-1,1),x_sx.reshape(-1,1)))
# Preparing velocity model
v0 = 2.; # Velocity at the origin of the model
vergrad = 0.5; # Vertical gradient
horgrad = 0.; # Horizontal gradient
vs = v0 + vergrad*sz + horgrad*sx # Velocity at the source location
velmodel = vs + vergrad*(Z-sz) + horgrad*(X-sx);
y_train_o = np.true_divide(1.0,np.square(velmodel.reshape(-1,1)[selected_pts]))
y_train = np.append(y_train_o,np.true_divide(1.0,np.square(vs)))
# Preparing traveltime
# Traveltime solution
if vergrad==0 and horgrad==0:# For homogeneous velocity modelT_data = np.sqrt((Z-sz)**2 + (X-sx)**2)/v0;
else:# For velocity gradient modelT_data = np.arccosh(1.0+0.5*(1.0/velmodel)*(1/vs)*(vergrad**2 + horgrad**2)*((X-sx)**2 + (Z-sz)**2))/np.sqrt(vergrad**2 + horgrad**2)
# set interval of receiver -- deltaxr
deltaxr = deltax * 5
xr = np.arange(xmin,xmax+deltax,deltaxr)
xr_n = np.divide(xr,deltax).astype(int)
nr = xr.size
# set the true traveltime of receiver points
tt_rece = np.arange((xr.size),dtype = np.float64)
y_train_r = np.arange((xr.size),dtype = np.float64)
for i in range(xr.size):tt_rece[i] = T_data[0,xr_n[i]]y_train_r[i] = np.true_divide(1.0,np.square(velmodel[0,xr_n[i]].reshape(-1,1)))
z_sz_nr = np.arange((nr),dtype = np.float64)
x_sx_nr = np.arange((nr),dtype = np.float64)
for i in range(nr):z_sz_nr[i] = szx_sx_nr[i] = sx
Zf_r = Z.reshape(-1,1)[xr_n]
Xf_r = X.reshape(-1,1)[xr_n]
# input data of receiver location x z and xs zs
x_train_r = np.hstack((Zf_r.reshape(-1,1),Xf_r.reshape(-1,1),z_sz_nr.reshape(-1,1),x_sx_nr.reshape(-1,1)))四、用Pytorch搭建PINN网络
1.网络搭建
代码如下:
class DNN(nn.Module):def __init__(self,layers):super().__init__()'Initialise neural network as a list using nn.Modulelist' self.linears = nn.ModuleList([nn.Linear(layers[i], layers[i+1]) for i in range(len(layers)-1)]) self.iter = 0#Elu和ReLU均为非线性的激活函数。如果只有线性层,那么相当于输出只是输入做了了线性变换的结果,对于线性回归没有问题。但是程函方程求解我们需要加入激活函数使输出的结果具有非线性的特征self.elu = nn.ELU() self.relu = nn.ReLU()def forward(self,d):#d就是整个网络的输入if torch.is_tensor(d) != True: d = torch.from_numpy(d)a = d.float()for i in range(len(layers)-2):z = self.linears[i](a) a = self.relu(z) a = self.linears[-1](a)return a
2.一些基本参数变量的确定以及数据格式的转换
代码如下:
device = torch.device("cuda") #在跑深度学习的时候最好使用GPU,这样速度会很快。不要的话默认用cpu跑
epochs = 10000 #这是迭代次数,把所有的训练数据输入到网络里去就叫完成了一次epoch。
learningrate = 2e-4 #学习率,相当于优化算法里的步长,学习率越大,网络参数更新地更加激进。学习率越小,网络学习地更加稳定。
layers = [4,50,50,50,50,50,50,50,50,50,50,2,2,25,25,25,25,25,25,25,1] #网络每一层的神经元个数,[1,10,1]说明只有一个隐含层,输入的变量是一个,也对应一个输出。如果是两个变量对应一个输出,那就是[2,10,1]
net = DNN(layers).to(device=device) #网络的初始化
print(net)
optimizer = torch.optim.Adam(net.parameters(), lr=learningrate)#优化器,不同的优化器选择的优化方式不同,这里用的是随机梯度下降SGD的一种类型,Adam自适应优化器。需要输入网络的参数以及学习率,当然还可以设置其他的参数
l1loss = nn.L1Loss() #损失函数,这里选用的是MSE。损失函数也就是用来计算网络输出的结果与对应的标签之间的差距,差距越大,说明网络训练不够好,还需要继续迭代。
mseloss = nn.MSELoss(reduction='mean')
MinTrainLoss = 1e10
train_loss =[] #用一个空列表来存储训练时的损失,便于画图
y_zero = np.zeros(num_tr_pts+1)
#因为涉及到梯度计算,Pytorch提供了autograd可以用来很方便的计算
#我们必须把用numpy定义的变量转换成tensor,用Variable定义并设置requires_grad=True则代表需要求梯度的参数
pt_x_train = Variable(torch.from_numpy(np.array(x_train)),requires_grad=True).to(device=device,dtype = torch.float32).reshape(-1,4) #这里需要把我们的训练数据转换为pytorch tensor的类型,并且把它变成gpu能运算的形式。
pt_y_train = Variable(torch.from_numpy(np.array(y_train)),requires_grad=False).to(device=device,dtype = torch.float32).reshape(-1,1) #reshap的目的是把维度变成(25,1),这样25相当于是batch,我们就可以一次性把所有的点都输入到网络里去,最后网络输出的结果也不是(1,1)而是(25,1),我们就能直接计算所有点的损失
pt_y_train_zero = Variable(torch.from_numpy(np.array(y_zero)),requires_grad=False).to(device=device,dtype = torch.float32).reshape(-1,1) #
pt_x_train_r = Variable(torch.from_numpy(np.array(x_train_r)),requires_grad=True).to(device=device,dtype = torch.float32).reshape(-1,4)
pt_rece_true = Variable(torch.from_numpy(np.array(tt_rece)),requires_grad=False).to(device=device,dtype = torch.float32).reshape(-1,1)
pt_y_train_r = Variable(torch.from_numpy(np.array(y_train_r)),requires_grad=False).to(device=device,dtype = torch.float32).reshape(-1,1) #resh
print(pt_x_train.dtype)
print(pt_x_train.shape)
五、用Pytorch搭建PINN网络
start = time.time()
start0=time.time()
for epoch in range(1,epochs+1):net.train() #net.train():在这个模式下,网络的参数会得到更新。对应的还有net.eval(),这就是在验证集上的时候,我们只评价模型,并不对网络参数进行更新。pt_y_pred = net(pt_x_train) #将tensor放入网络中得到预测值#此处调用了pytorch的autograd来进行自动微分计算梯度,pt_y_pred为函数y,pt_x_train为自变量u_tx = torch.autograd.grad(pt_y_pred, pt_x_train, grad_outputs=torch.ones_like(pt_y_pred),create_graph=True, allow_unused=True)[0] # 求偏导数delta_tx = u_tx[:, 1].unsqueeze(-1)delta_tz = u_tx[:, 0].unsqueeze(-1)delta_txz = delta_tx**2+delta_tz**2#loss1 为程函方程部分loss1 = mseloss(delta_txz,pt_y_train) #用mseloss计算预测值和对应标签的差别#loss1_1 定义了边界条件,即炮点处的走时为0loss1_1 = torch.abs(pt_y_pred[10201,0])pt_y_pred_r = net(pt_x_train_r) #将tensor放入网络中得到预测值#loss2 为数据拟合项,在检波点处必须满足观测走时loss2 = mseloss(pt_y_pred_r,pt_rece_true) #用mseloss计算预测值和对应标签#loss3 限制预测出来的走时场必须为正值y_heaviside = torch.mul(torch.sub(1,torch.sign(pt_y_pred)),torch.abs(pt_y_pred))loss3 = mseloss(y_heaviside,pt_y_train_zero)# 最后把所有的loss相加,用于统一反传梯度loss = loss1 + 10*loss1_1 + loss3 + 10*loss2optimizer.zero_grad() #在每一次迭代梯度反传更新网络参数时,需要把之前的梯度清0,不然上一次的梯度会累积到这一次。loss.backward() # 反向传播optimizer.step() #优化器进行下一次迭代if epoch % 10 == 0:#每10个epoch保存一次lossend = time.time()print("epoch:[%5d/%5d] time:%.2fs current_loss:%.5f loss1:%.5f loss1_1:%.5f loss3:%.5f loss2:%.5f"%(epoch,epochs,(end-start),loss.item(),loss1.item(),loss1_1.item(),loss3.item(),loss2.item()))start = time.time()train_loss.append(loss.item())if train_loss[-1] < MinTrainLoss:torch.save(net.state_dict(),"model.pth") #保存每一次loss下降的模型MinTrainLoss = train_loss[-1]
end0 = time.time()
print("训练总用时: %.2fmin"%((end0-start0)/60))六、查看loss下降情况
plt.plot(range(epochs),train_loss)
plt.xlabel("epoch")
plt.ylabel("loss")七、导入网络模型,输入验证数据,预测结果
ztest_sz = np.arange((Z.reshape(-1,1)).size,dtype = np.float)
xtest_sx = np.arange((Z.reshape(-1,1)).size,dtype = np.float)
for i in range((Z.reshape(-1,1)).size):ztest_sz[i] = szxtest_sx[i] = sx
X_star = [Z.reshape(-1,1), X.reshape(-1,1)] # Grid points for training
x_test = np.hstack((Z.reshape(-1,1),X.reshape(-1,1),ztest_sz.reshape(-1,1),xtest_sx.reshape(-1,1)))pt_x_test = torch.from_numpy(x_test).to(device=device,dtype=torch.float32).reshape(-1,4)
Dnn = DNN(layers).to(device)
Dnn.load_state_dict(torch.load("model.pth",map_location=device))#pytoch 导入模型
Dnn.eval()#这里指评价模型,不反传,所以用eval模式
pt_y_test = Dnn(pt_x_test)
y_test = pt_y_test.detach().cpu().numpy()#输出结果torch tensor,需要转化为numpy类型来进行可视化
T = y_test[:,0].reshape(Z.shape)八、对比画图
1、画出预测走时场
plt.style.use('default')plt.figure(figsize=(4,4))ax = plt.gca()
im = ax.imshow(np.abs(T), extent=[xmin,xmax,zmax,zmin], aspect=1, cmap="jet")plt.xlabel('Offset (km)', fontsize=14)
plt.xticks(fontsize=10)plt.ylabel('Depth (km)', fontsize=14)
plt.yticks(fontsize=10)ax.xaxis.set_major_locator(plt.MultipleLocator(0.5))
ax.yaxis.set_major_locator(plt.MultipleLocator(0.5))divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="6%", pad=0.15)cbar = plt.colorbar(im, cax=cax)cbar.set_label('seconds',size=10)
cbar.ax.tick_params(labelsize=10)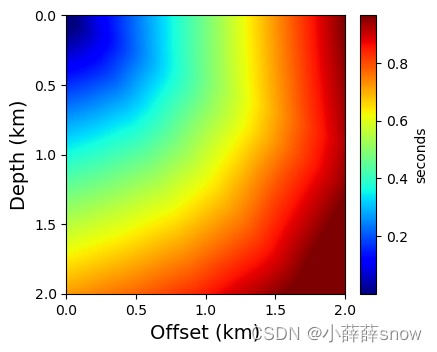
2、画出真实走时场
plt.style.use('default')plt.figure(figsize=(4,4))ax = plt.gca()
im = ax.imshow(np.abs(T_data), extent=[xmin,xmax,zmax,zmin], aspect=1, cmap="jet")plt.xlabel('Offset (km)', fontsize=14)
plt.xticks(fontsize=10)plt.ylabel('Depth (km)', fontsize=14)
plt.yticks(fontsize=10)ax.xaxis.set_major_locator(plt.MultipleLocator(0.5))
ax.yaxis.set_major_locator(plt.MultipleLocator(0.5))divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="6%", pad=0.15)cbar = plt.colorbar(im, cax=cax)cbar.set_label('seconds',size=10)
cbar.ax.tick_params(labelsize=10)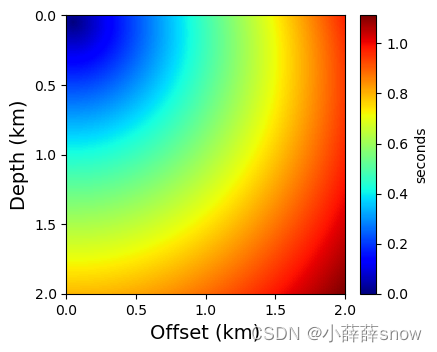
总结
以上是如何利用PINN网络求解程函方程的全部内容,同时这也是对于如何利用PINN解偏微分方程的一个应用。