大家好,我是拉斯,今天分享一个爬取某音视频的一个小案例,大家一起学习

目录
- 前言
- 基本环境配置
- 爬取目标视频
- 获取视频链接
- 1.查看网页源代码
- 2.抓包工具捕捉
- 下载视频(以mp4格式进行保存)
- 获取其他信息并打印(作者名,作品名,获赞数......)
- 示例(获取作者名)
- 代码
- 成果
- 完结啦
前言
前面已经发布了爬取4k高清图片的示例,大家可以去参考学习;本次使用selenium和request技术,获取所想爬取的数据。
原视频 作者名 作品名 获赞数 评论数 收藏数 转发数
基本环境配置
- 版本:Python3
- 系统:Windows
- 相关模块:selenium,time,requests
- 开发工具:Pycharm
爬取目标视频
获取视频链接
1.查看网页源代码
一如既往搜索video标签,发现没有;再搜索video,发现也没有。这时候换思路,用开发者工具.
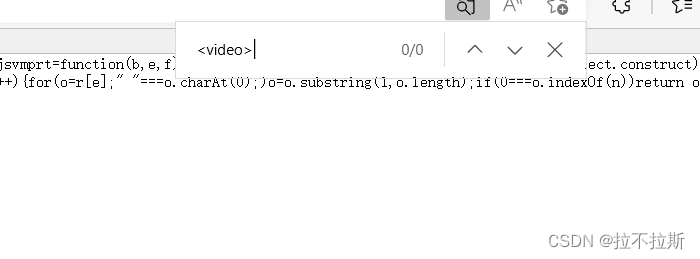

2.抓包工具捕捉
注:对不起大家,下面这张图三个链接都是可以到原视频的,因此都可以作为第一段代码的url来使用!!!

下载视频(以mp4格式进行保存)
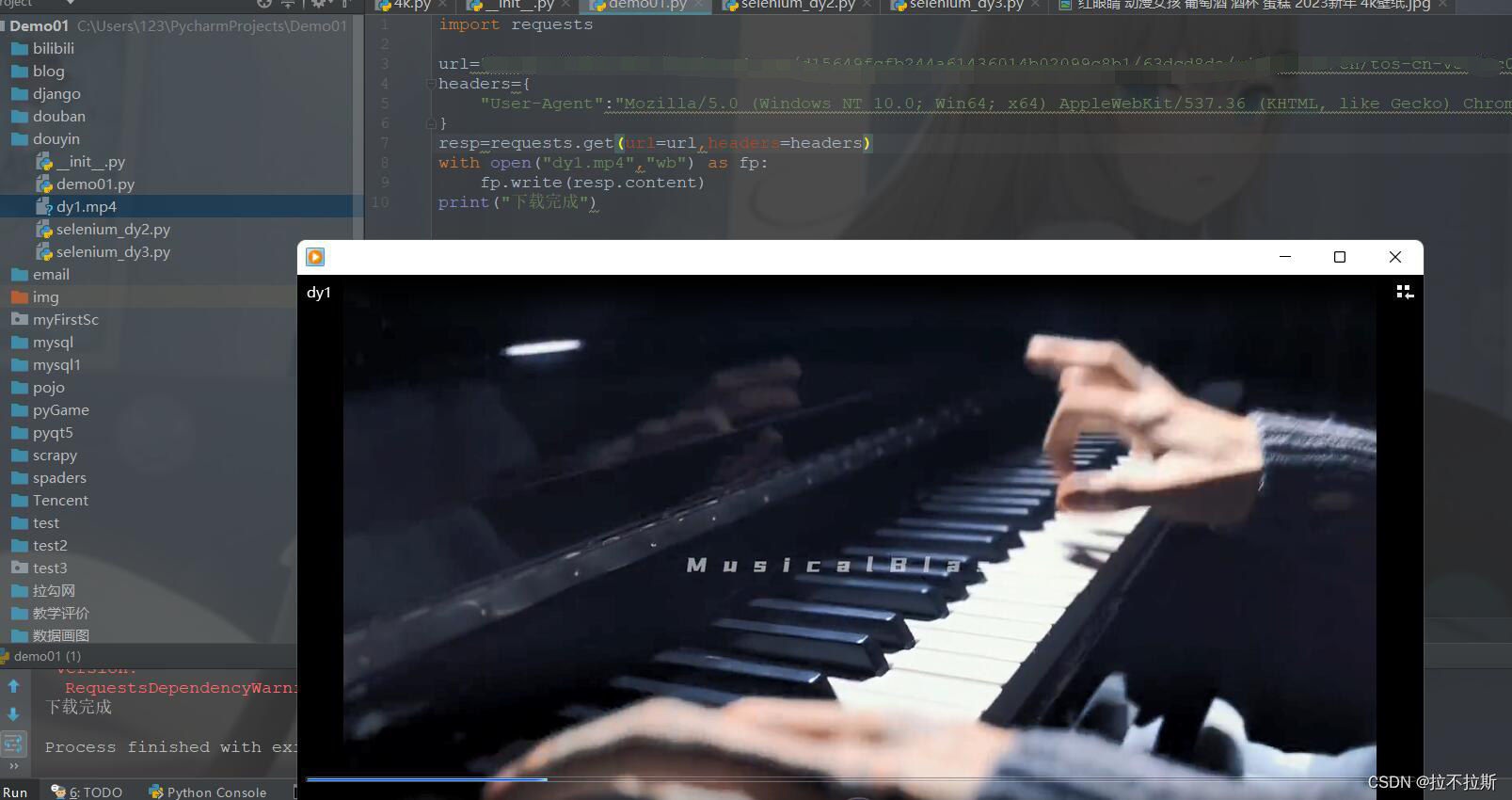
既然有了视频的链接,就可以直接发起请求进行视频的下载,以mp4格式进行持久化存储
代码:(requests技术进行视频下载)
import requestsurl="url1" #特别注意:此处url1值为上面图片三个链接中任意一个,会变化所以不写死,大家得到后自行复制到此处 headers={"User-Agent":"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/109.0.0.0 Safari/537.36 Edg/109.0.1518.70" } resp=requests.get(url=url,headers=headers) with open("dy1.mp4","wb") as fp:fp.write(resp.content) print("下载完成")成果:
获取其他信息并打印(作者名,作品名,获赞数…)
使用selenium技术进行元素定位,复制xpath,即可使用find_element_by_xpath方法进行内容获取,后面每一个都是这样获取,下面以作者名为例子
示例(获取作者名)
抓包工具进行作者名定位,最后右击元素复制对应xpath.

复制xpath:

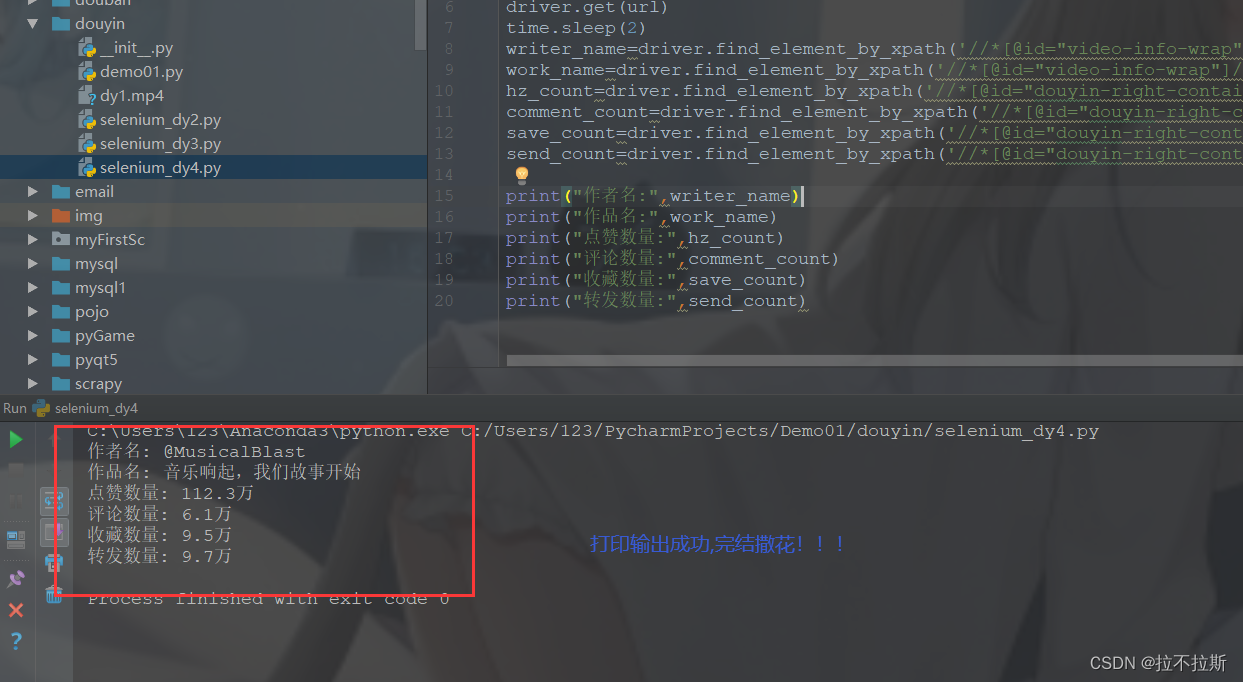
代码
from selenium import webdriver import time from selenium.webdriver.common.keys import Keys url="url2" #url2值在评论区获得,因为写上审核不给过 driver=webdriver.Chrome() driver.get(url) time.sleep(2) writer_name=driver.find_element_by_xpath('//*[@id="video-info-wrap"]/div[1]/div[1]/div[1]/span/span/span/span/span/span/span').text #作者名 work_name=driver.find_element_by_xpath('//*[@id="video-info-wrap"]/div[1]/div[2]/div/div/span/span/span[1]/span/span/span').text #作品名 hz_count=driver.find_element_by_xpath('//*[@id="douyin-right-container"]/div[3]/div[4]/div[2]/div[1]/div/div/div[1]/div[2]/div[2]/div/div[2]').text #获赞数量 comment_count=driver.find_element_by_xpath('//*[@id="douyin-right-container"]/div[3]/div[4]/div[2]/div[1]/div/div/div[1]/div[2]/div[3]/div/div[2]').text #评论数量 save_count=driver.find_element_by_xpath('//*[@id="douyin-right-container"]/div[3]/div[4]/div[2]/div[1]/div/div/div[1]/div[2]/div[4]/div/div[2]').text #收藏数量 send_count=driver.find_element_by_xpath('//*[@id="douyin-right-container"]/div[3]/div[4]/div[2]/div[1]/div/div/div[1]/div[2]/div[5]/div[1]/div/div[2]').text #转发数量print("作者名:",writer_name) print("作品名:",work_name) print("点赞数量:",hz_count) print("评论数量:",comment_count) print("收藏数量:",save_count) print("转发数量:",send_count)成果
完结啦