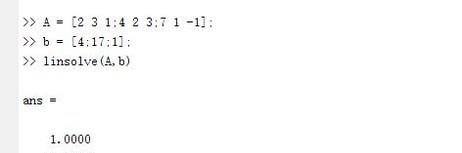参考：mathematica.pdf
参考：MATHEMATICA微分方程.pdf
数学微分方程，第三版，有两个目的。
首先，我们介绍和讨论在典型的本科和研究生课程中所涵盖的主题，包括拉普拉斯变换、傅立叶级数、特征值问题和边值问题。其次，我们说明了如何使用Mathematica来增强微分方程的研究，不仅通过消除计算困难，而且通过克服与微分方程的显式解相关的视觉限制，这往往是相当复杂的。
在每一章中，我们首先以类似于大多数微分方程文本的方式简要地介绍材料，然后说明Mathematica可以用来解决一些典型问题。
例如，在第二章中，我们介绍一阶方程的主题。首先，我们展示了如何手工解决某些类型的问题，然后展示了如何使用Mathematica来辅助相同的解决过程。最后，我们说明了如何使用像DSolve和NDSolve这样的Mathematica命令来精确地和/或数值地解决一些经常遇到的方程。
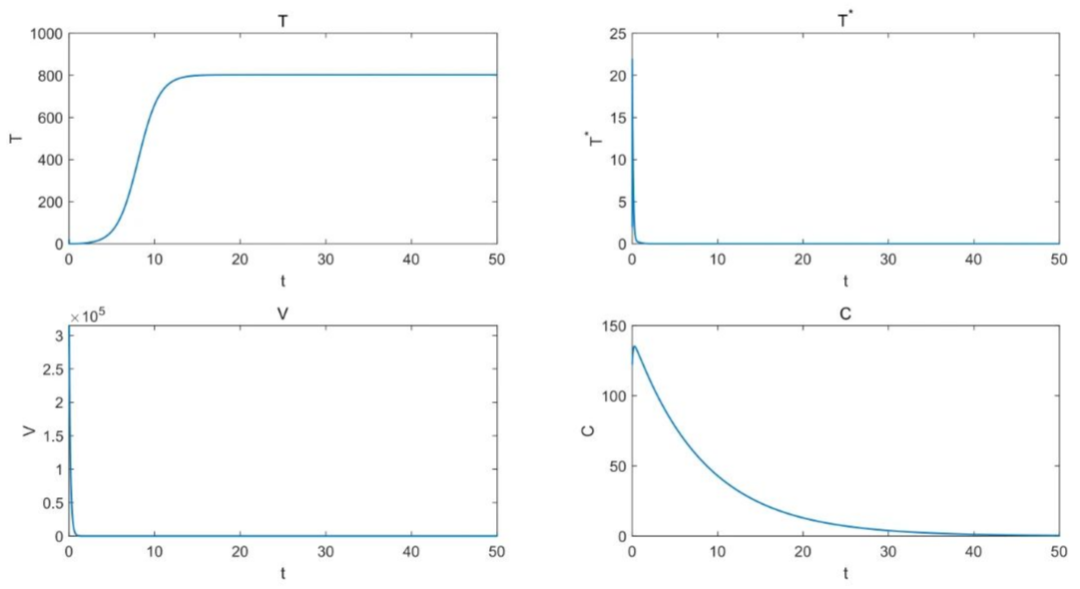
第三章讨论了一阶方程的一些应用。由于我们有经验并且了解第二章的解决方法，所以我们使用DSolve和类似的命令来获取解决方案。这样做，我们能够强调应用程序本身，而不是陷入计算。在微分方程的研究中使用Mathematica的优势有很多，但最有用的可能是能够生成与微分方程解相关的图形。这在应用程序的讨论中尤其有益，因为许多物理情况都是如此用微分方程建模。例如，我们会看到，摆的运动可以用微分方程来模拟。当我们解决摆的运动问题时，我们使用技术来实际观察摆的运动。对于附着在弹簧末端的物体的运动，以及许多其他问题，也是如此。有了这种能力，研究微分方程就变得更有意义，也更有趣了。
如果您是Mathematica的初级用户，特别是5.0版的新用户，附录包含了Mathematica的介绍，包括关于输入和计算命令、加载包以及利用Mathematica的广泛帮助工具的讨论。虽然第1章篇幅很短，但是第1章介绍了将在后续章节中研究的例子。此外，在第一章中介绍的词汇将在整个文本中使用。因此，尽管在很大程度上可以快速阅读，但后面的章节将利用这里讨论的术语和技术。

第一章 微分方程导论

第1章。微分方程导论

第二章。First-OrderOrdinary DifferentialEquations-一阶常微分方程

参考：利用Methematica推导一阶线性微分方程

齐次方程

非齐次方程

DSolve[D[y[x], x] + p[x] y[x] == q[x], y[x], x]

Chapter 3 应用一阶常微分方程

第四章 高阶微分方程

第5章。高阶微分方程的应用

第六章。常用微分方程系统

第七章。常微分方程组的应用

第八章。拉普拉斯变换方法

第9章。特征值问题和傅立叶级数

第十章。偏微分方程

求解数值方程组

Solve[{a x + b y == 1, x - y == 2}, {x, y}]

注：N个变量，N-1个方程才有解。

Solve[{l1 + lm == k1, l2 + lm == k2, l1 + (l2 lm/(l2 + lm)) == k3, 
l2 + (l1 lm/(l1 + lm)) == k4}, {l1, l2, lm}]
(*有N个变量，N个方程*)

Solve[{l1 + lm == k1, l2 + lm == k2, 
l1 + (l2 lm/(l2 + lm)) == k3}, {l1, l2, lm}]

输出两种解。

Mathematica求解微分方程组

参考：【Mathematica】一个微分方程组的求解和作图

sol = DSolve[{x'[t] + y[t] == 1, y'[t] + x[t] == 2}, {x[t], y[t]}, t]
sol = DSolve[{x'[t] + y[t] == a, y'[t] + x[t] == b}, {x[t], y[t]}, t]
Simplify[sol]