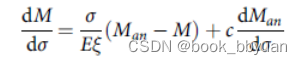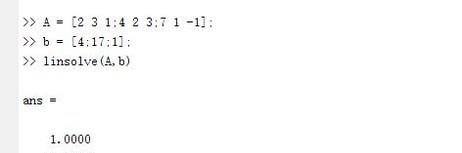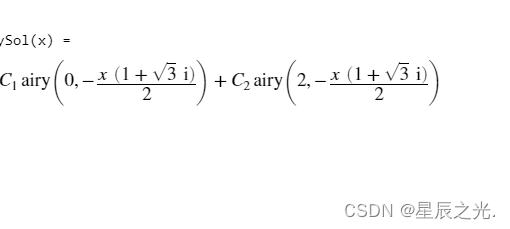MATLAB用solve求解普通二元高次方程

先说问题：
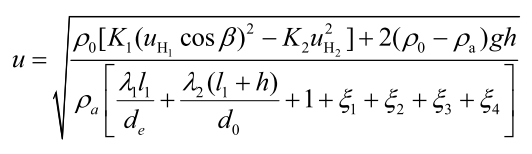
在这里插入图片描述
有这两个式子，其中除了u和λ，其他都是已知参数。所以，不必恐慌，看着很复杂，但是这个条件一加，其实就是很简单的二元高次方程组，把2式带到1式，然后用MATLAB自带的solve函数一解就出来了。

我的MATLAB代码如下：

function[u,lamda]=fun()
clear
syms u lamda_1;
syms rho_a rho_0 xi_1 xi_2 xi_3 xi_4 xi_5 xi_6 l_1 l_2 l_3 l_4 l_5 d k_1 k_2 u_H1 u_H2 cos_beta g h
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%输入基本参数
rho_a=0.7; rho_0=0.9;
xi_1=0.5; xi_2=0.5; xi_3=0.5; xi_4=0.5; xi_5=0.5; xi_6=0.5;
l_1=1; l_2=1; l_3=1; l_4=1; l_5=1;
d=0.21;
k_1=0.7; k_2=-0.8  ; 
u_H1=1.2; u_H2=1.0; 
cos_beta=1;
g=10;
h=1;
k=0.3;
v=3e-5;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%方程1化简系数
a_1=rho_a*(1+xi_1+xi_2+xi_3+xi_4+xi_5+xi_6);
b_1=(l_1+l_2+l_3+l_4+l_5)/d;
c_1=rho_0*(k_1*(u_H1*cos_beta)*(u_H1*cos_beta)-k_2*u_H2*u_H2)+2*(rho_0-rho_a)*g*h;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%解方程
%%最终把方程化成(a_1+b_1*lamda)*u^2=c_1的形式
eq1=(a_1+b_1*0.11*(k/d+68*v/(u*d))^(0.25))*u^2-c_1;
u=double(solve(eq1,u))
%%再将u带回求解lamda
eq2=lamda_1-(0.11*(k/d+68*v/(u*d)).^(0.25));
lamda=double(solve(eq2,lamda_1))

一个小技巧就是用a,b,c 把比较复杂的一坨参数看做一个整体，反正都是已知量，不影响。
然后把2式λ带到1式中，那1式就是关于u的一元高次方程，用solve求解即可；
double的意思是把solve的结果表示成double类型
在这里插入图片描述

关于solve函数的扩展与该问题的补充说明

1.首先是对方程的求解

在这里插入图片描述

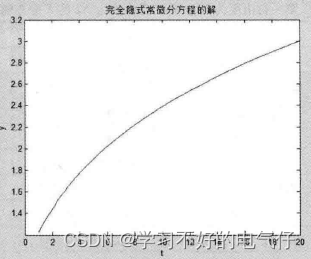
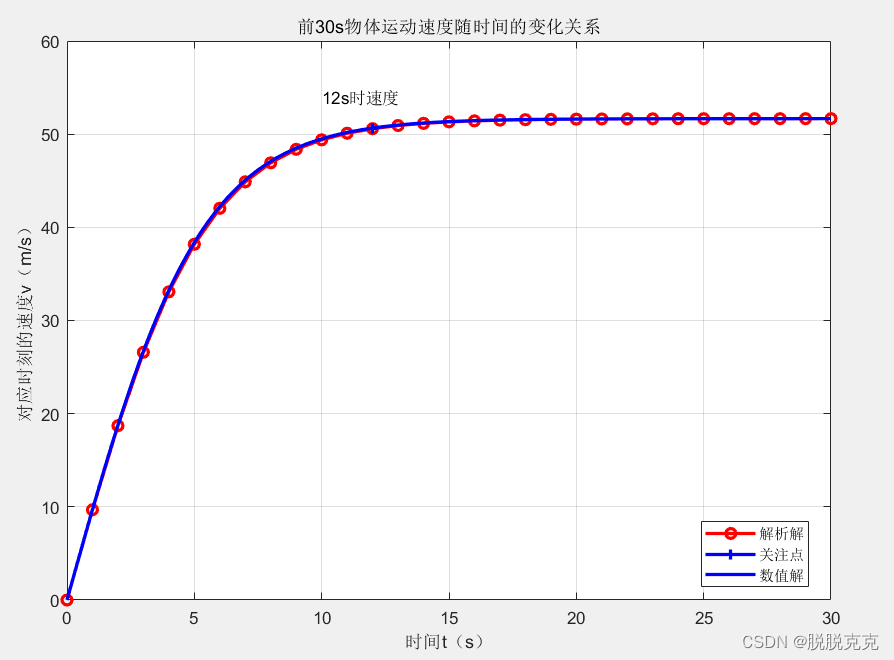
完美的算出了方程的解
现在对上面的代码进行一些说明

1.syms x；是必要的，这将会把x设为符号变量。
2.eq=x^2 +2x+1;eq也会变为一个符号变量用于储存方程
x^ 2+2x+1
2.s=solve(eq,x)；中方程的结果由solve函数返回，存储在s里。注意（eq，x）中x是说明eq这个方程中x为变量。
这个看起来没有什么用但是对下面这个方程就有些意思了：
a*x+2=0
如果把a看为变量的话方程的解就是-2/x。
如果把x看为变量的话方程的解就是-2/a。
我们看一下下面的结果：
在这里插入图片描述
是不是很有意思？