B树的原理与CPP实现

B树是一种自平衡的多叉树数据结构，广泛应用于数据库系统和文件系统中。其设计初衷是为了在存储设备上实现高效的读写操作，特别是在磁盘存储或其他大规模存储场景下。B树的每个节点可以有多个子节点，这与二叉树不同，B树能有效减少树的高度，从而减少数据检索时磁盘的I/O操作次数。

本文将详细介绍B树的性质，以及它的查找、插入和删除操作。

一、B树的基本性质

节点的键值数量范围

每个节点的键值数量是有范围的，假设B树的阶（T），则每个节点中包含的键值数必须在T - 1 到 2 * T - 1 之间。

根节点特例

根节点至少包含1个键值（除非整个树为空），其他节点至少包含T - 1个键值。

子树数量限制

每个节点最多拥有 m 个子节点，且子节点的数量与节点的键值数量相关，假设某个节点有 k 个键值，则它会有 k+1 个子节点。

键值有序性

每个节点中的键值按从小到大的顺序排列。假设某节点中的键为 [k1, k2, ..., kn]，则：

所有左子树中的键值都小于k1；
所有右子树中的键值都大于kn；
中间子树中的键值介于相应的键值之间。

树的平衡性

B树是一棵严格平衡的树，所有叶子节点都位于同一层。这意味着树的高度始终保持较小，从而保证了良好的性能。

二、查找

查找过程描述

从根节点出发，找到键值所在的节点。由于节点内的键值是有序的，可以使用二分查找来定位。
递归或下朔
- 如果目标键值存在于当前节点，则查找成功。
- 如果目标键值不在当前节点，则根据当前节点的键值范围，选择对应的子节点进行递归查找，直到找到叶子节点。
叶子节点查找
- 如果在叶子节点中找到了目标键值，则查找成功。
- 如果叶子节点中没有找到目标键值，则查找失败。

示例

B树可以看做是一个多叉平衡搜索树，那么其查找与二叉平衡搜索树也就是相似的，例如下面的B树：

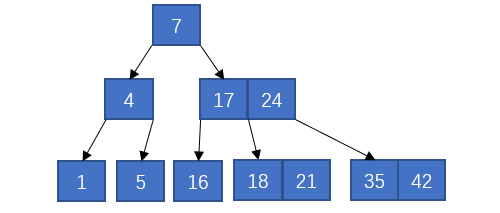
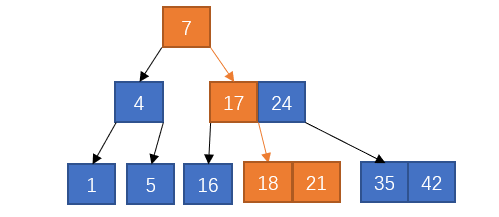
想要查找21这个值，那么在root节点，可以看到其比7大，所以到第二层第二个节点接着查找，可以看到比17大比24小，所以到第三层第四个节点接着查找，可以看到比18大，等于21，最终找到了这个值。

最终的比较路径就是

三、插入

插入过程描述

在B树的插入操作过程中，必须遵循以下规则来保持B树的平衡性和性质：

从根节点开始，沿着树的路径选择合适的子树，直到找到合适的叶子节点。
元素必须插入到叶子节点中。如果叶子节点未满，直接插入并结束操作。
如果插入时叶子节点已满（即包含m-1个键值，m为B树的阶数），则需要对该叶子节点进行分裂：
- 将中间键上移到父节点。
- 将该节点分裂为两个子节点，每个节点大约包含一半的键值。
父节点满时的递归分裂
- 如果父节点在插入中间键时也满了，继续将中间键上移并分裂父节点。
- 这种操作可以递归进行，甚至导致根节点的分裂。若根节点分裂，则树的高度增加一层。

这些规则保证了B树始终保持平衡，从而维持其高效的搜索、插入和删除操作。

示例

B树的插入一定是插入到叶子结点上。假设现在有一个度为 $T = 2$ 的B树，那么一个B树节点最多只能存在 $2 * T - 1 = 3$ 个键，假设我们先从根节点开始插入，依次插入

{1,5,7,4,16,35,24,42,21,17,18}

当节点满了就会产生上溢出，例如先插入1、5、7、4这四个元素值，这里根节点满了，最多只能存放3个键，这里却存放了4个，所以需要分裂

分裂完就如下图所示

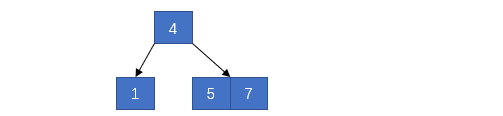
此时，根节点和两个叶子结点都满足要求，接着插入16和35，全部会插入到右边的节点上，如下图

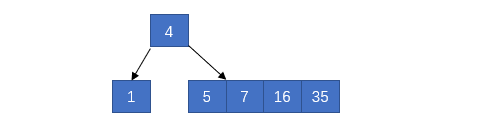
又产生了上溢出，和上次的处理手段一样，拆分右边的叶子结点

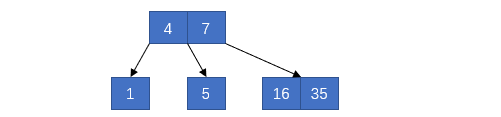
接着插入24和42

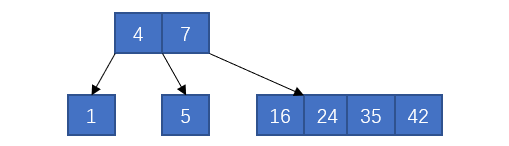
又产生了上溢出，和之前的手段，拆分产生上溢出的节点

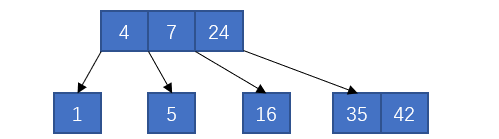
接着插入21、17和18

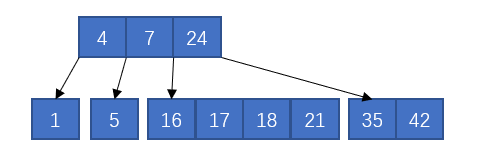
最底层第三个节点产生了上溢出，那么就处理这个节点

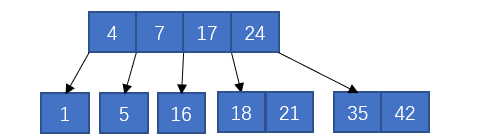
但是此时根节点也溢出了，那么就处理根节点

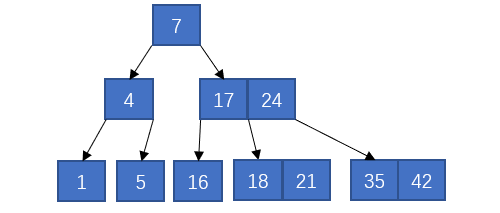
可以看到，通过这种方式，插入时只插入到叶子结点，就可以维持树一直是一个平衡树。

四、删除

B树的删除过程相较于插入要略显复杂一些，主要是如何维护B树的平衡与搜索树的性质。

删除过程描述

从根节点找到要删除的键
- 首先从根节点开始，沿着树的路径找到要删除的键
- 如果删除的键在叶子节点中，那么直接删除该键
- 如果删除的键不在叶子节点中，则需要特殊处理
删除键
- 删除叶子结点中的键
  - 如果删除后叶子节点的键数仍然不少于 $T - 1$ ，那么直接删除即可
  - 如果删除后叶子结点的键数少于 $T - 1$ ，那么需要借用或者合并
- 删除内部节点中的键
  - 前驱法：用该键的左子树的最大键替代该键，然后删除该最大键（该最大键一定位于叶子节点中，因而转换为删除叶子节点中的键）。
  - 后继法：用该键的右子树的最小键替代该键，然后删除该最小键（同样，最小键在叶子节点中，最终也变成删除叶子节点中的键）。
借用或合并
- 如果删除后节点的键数少于 $T - 1$ ，且该节点有兄弟节点（左兄弟或右兄弟）拥有多于 $T - 1$ 个键，那么可以从兄弟节点借一个键过来。从父节点中借用一个键下来到当前节点，兄弟节点中的一个键上移到父节点，以保持B树的平衡。
- 如果兄弟节点没有多余的键可借用，则需要将当前节点与其兄弟节点合并：
  - 将当前节点、兄弟节点以及它们父节点中的分隔键合并成一个节点。
  - 这会导致父节点少一个键，如果父节点的键数少于 $T - 1$ ，需要进一步递归进行借用或合并操作，甚至可能导致根节点被删除。
根节点处理
- 如果根节点被删除，并且它没有任何键值了（即根节点只有一个子节点），则直接删除根节点，树的高度减小一层，新的根节点成为唯一的子节点。

示例

假设我们有下面一个T=3的B树，即5阶B树

我们要依次删除

{45,68,53,30,41,70}

首先删除45，查找45，可以发现是根节点，删除根节点的问题可以转换成删除叶子结点的问题，查找到45的后驱节点，是46，将46设置为根节点，删除45即可，此时叶子结点也满足最少为2的要求，不需要合并或者借用，此时为

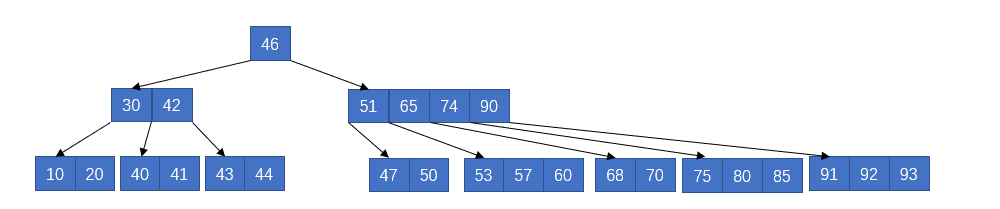
再删除68，删除完之后可以发现，这个叶子结点只有一个键了，这是不允许的

但是他的兄弟节点，前面的和后面的都可以借，此时可以借用一个就完成了平衡，这里我们向前借用一个

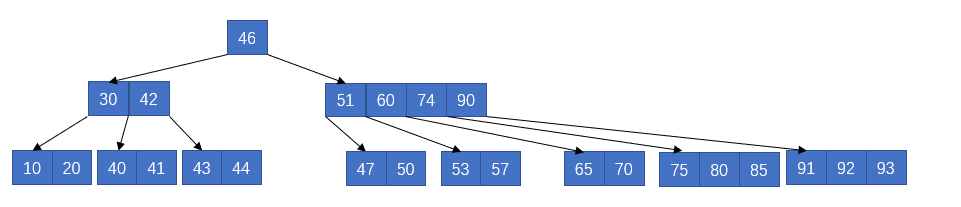
再删除53，发现又一个需要合并或者借用的

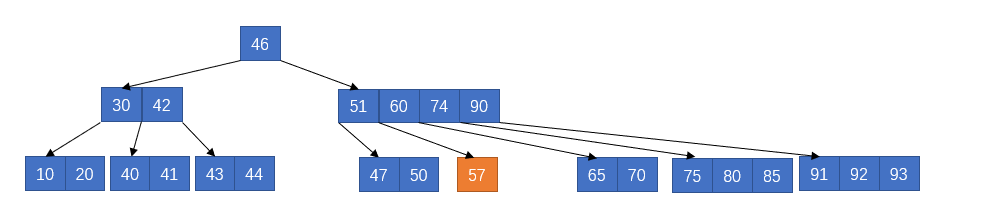
但是此时左右的兄弟节点无法借用，只能合并，这里的合并我们与前驱节点合并

再删除30，删除30的时候首先他不是叶子结点，需要转化为删除叶子节点的问题，我们找到他的后继节点40，替换30的位置再删除40。

此时的41的叶子节点不满足要求，他的前面的兄弟节点和后面的兄弟节点都没法借用，所以可以执行合并操作了，将当前节点、兄弟节点以及它们父节点中的分隔键合并成一个节点，这里我们合并后一个兄弟节点。

此时40的位置又不满足要求了，产生了下溢出，那么再借用一个即可

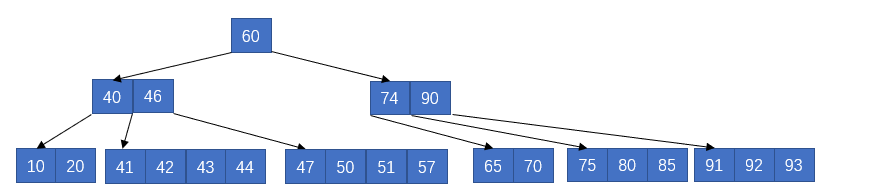
最后删除70，向右边的兄弟节点借一个即可。

五、代码

#include <iostream>
#include <vector>
using namespace std;// B树节点
class Node {
public:vector<int> keys;    // 节点中的键vector<Node*> children; // 子节点指针bool isLeaf;         // 判断是否为叶节点int t;               // B树的最小度数Node(int _t, bool _isLeaf) {t = _t;isLeaf = _isLeaf;}// 在子树中查找键Node* search(int key) {int i = 0;while (i < keys.size() && key > keys[i])i++;if (i < keys.size() && keys[i] == key)return this;if (isLeaf)return nullptr;return children[i]->search(key);}// 分裂子节点void splitChild(int i, Node* y) {Node* z = new Node(y->t, y->isLeaf);z->keys.resize(t - 1);for (int j = 0; j < t - 1; j++)z->keys[j] = y->keys[j + t];if (!y->isLeaf) {z->children.resize(t);for (int j = 0; j < t; j++)z->children[j] = y->children[j + t];}y->keys.resize(t - 1);children.insert(children.begin() + i + 1, z);keys.insert(keys.begin() + i, y->keys[t - 1]);}// 插入非满节点void insertNonFull(int key) {int i = keys.size() - 1;if (isLeaf) {keys.insert(keys.begin() + (i + 1), key);while (i >= 0 && keys[i] > key) {keys[i + 1] = keys[i];i--;}keys[i + 1] = key;} else {while (i >= 0 && keys[i] > key)i--;if (children[i + 1]->keys.size() == 2 * t - 1) {splitChild(i + 1, children[i + 1]);if (keys[i + 1] < key)i++;}children[i + 1]->insertNonFull(key);}}// 从节点中删除键void remove(int key) {int idx = findKey(key);if (idx < keys.size() && keys[idx] == key) {if (isLeaf)removeFromLeaf(idx);elseremoveFromNonLeaf(idx);} else {if (isLeaf) {cout << "Key " << key << " is not in the tree.\n";return;}bool flag = (idx == keys.size());if (children[idx]->keys.size() < t)fill(idx);if (flag && idx > keys.size())children[idx - 1]->remove(key);elsechildren[idx]->remove(key);}}// 辅助函数int findKey(int key) {int idx = 0;while (idx < keys.size() && keys[idx] < key)++idx;return idx;}void removeFromLeaf(int idx) {keys.erase(keys.begin() + idx);}void removeFromNonLeaf(int idx) {int key = keys[idx];if (children[idx]->keys.size() >= t) {int pred = getPredecessor(idx);keys[idx] = pred;children[idx]->remove(pred);} else if (children[idx + 1]->keys.size() >= t) {int succ = getSuccessor(idx);keys[idx] = succ;children[idx + 1]->remove(succ);} else {merge(idx);children[idx]->remove(key);}}int getPredecessor(int idx) {Node* cur = children[idx];while (!cur->isLeaf)cur = cur->children[cur->keys.size()];return cur->keys[cur->keys.size() - 1];}int getSuccessor(int idx) {Node* cur = children[idx + 1];while (!cur->isLeaf)cur = cur->children[0];return cur->keys[0];}void fill(int idx) {if (idx != 0 && children[idx - 1]->keys.size() >= t)borrowFromPrev(idx);else if (idx != keys.size() && children[idx + 1]->keys.size() >= t)borrowFromNext(idx);else {if (idx != keys.size())merge(idx);elsemerge(idx - 1);}}void borrowFromPrev(int idx) {Node* child = children[idx];Node* sibling = children[idx - 1];child->keys.insert(child->keys.begin(), keys[idx - 1]);if (!child->isLeaf)child->children.insert(child->children.begin(), sibling->children[sibling->keys.size()]);keys[idx - 1] = sibling->keys[sibling->keys.size() - 1];sibling->keys.pop_back();if (!sibling->isLeaf)sibling->children.pop_back();}void borrowFromNext(int idx) {Node* child = children[idx];Node* sibling = children[idx + 1];child->keys.push_back(keys[idx]);if (!child->isLeaf)child->children.push_back(sibling->children[0]);keys[idx] = sibling->keys[0];sibling->keys.erase(sibling->keys.begin());if (!sibling->isLeaf)sibling->children.erase(sibling->children.begin());}void merge(int idx) {Node* child = children[idx];Node* sibling = children[idx + 1];child->keys.push_back(keys[idx]);for (int i = 0; i < sibling->keys.size(); ++i)child->keys.push_back(sibling->keys[i]);if (!child->isLeaf) {for (int i = 0; i <= sibling->keys.size(); ++i)child->children.push_back(sibling->children[i]);}keys.erase(keys.begin() + idx);children.erase(children.begin() + idx + 1);delete sibling;}
};// B树类
class BTree {
private:Node* root;int t;public:BTree(int _t) {root = nullptr;t = _t;}// 查找键Node* search(int key) {return root == nullptr ? nullptr : root->search(key);}// 插入键void insert(int key) {if (root == nullptr) {root = new Node(t, true);root->keys.push_back(key);} else {if (root->keys.size() == 2 * t - 1) {Node* s = new Node(t, false);s->children.push_back(root);s->splitChild(0, root);int i = (s->keys[0] < key) ? 1 : 0;s->children[i]->insertNonFull(key);root = s;} else {root->insertNonFull(key);}}}// 删除键void remove(int key) {if (!root) {cout << "The tree is empty\n";return;}root->remove(key);if (root->keys.size() == 0) {Node* tmp = root;if (root->isLeaf)root = nullptr;elseroot = root->children[0];delete tmp;}}
};// 测试 B 树
int main() {BTree t(3); // B树的度数为3t.insert(10);t.insert(20);t.insert(5);t.insert(6);t.insert(12);t.insert(30);t.insert(7);t.insert(17);cout << "Traversal of tree after insertions:\n";if (t.search(6) != nullptr) cout << "Found 6\n";else cout << "Not Found 6\n";t.remove(6);cout << "Traversal of tree after removing 6:\n";if (t.search(6) != nullptr) cout << "Found 6\n";else cout << "Not Found 6\n";return 0;
}