影响力最大化：在社交网络中找到一小部分能够最大化传播影响力的节点(种子节点)。

一是改进原有的贪心算法，进一步缩短其运行时间
二是提出新的degree-discount（度折扣）启发式，改善影响传播。

实验结果表明:
（a）改进的贪心算法，在影响扩散匹配的情况下，获得了更好的运行时间
（b）程度折扣启发式比经典的基于程度和中心的启发式获得了更好的影响扩散;当对特定的影响级联模型进行优化时，与贪心算法的影响线程几乎匹配。
更重要的是
（c）在我们有几万个节点的实验图中，度离散计数启发式只在毫秒内运行，而即使是改进的贪婪算法也要运行数小时。

基于我们的结果，我们相信微调启发式可能为影响最大化问题提供真正可扩展的解决方案，具有令人满意的影响扩散和惊人的快速运行时间。

相关工作

社交网络是大规模的，具有复杂的连接结构，而且非常动态，这意味着问题的解决方案需要非常高效和可扩展。

1. Domingos和Richardson首先将影响最大化作为算法问题进行了研究。
   然而，他们的方法是概率的。
2. Kempe、Kleinberg和Tardos首先将该问题表述为以下离散优化问题。
   社交网络被建模为一个图，其中顶点代表个体，边代表两个个体之间的联系或关系。
   影响根据随机级联模型在网络中传播。
3. 中考虑了三种级联模型，分别是独立级联模型、权重级联模型和线性阈值模型。
   给定一个社交网络图，一个特定的影响级联模型，以及一个很小的k，影响最大化问题就是在图中找到k个顶点(称为种子)，使得在影响级联模型下，k个种子(文中称为影响扩散)所影响的顶点的期望数量最大。
4. Kempe等人证明了优化问题是np困难的，并提出了一种适用于所有三种模型的贪婪近似算法，该算法保证了影响扩散在最优影响扩散的(1−1/e)范围内。
   他们还通过实验表明，他们的贪婪算法在影响扩散方面明显优于经典的度和基于中心的启发式算法。
5. 然而，他们的算法有一个严重的缺点，那就是效率。
   他们的贪婪算法的一个关键元素是计算给定种子集的影响扩散，这被证明是一个困难的任务。
   他们没有找到一个精确的算法，而是对影响级联模型进行了足够多次的蒙特卡洛模拟，以获得对影响扩散的准确估计。
   因此，即使在一个中等规模的网络(例如15000个顶点)中找到一个小的种子集，在现代服务器上也可能需要几天的时间才能完成。
6. 最近的几项研究旨在解决这一效率问题。
   1）Kimura和Saito提出了基于最短路径的影响决策模型，并提供了在这些模型下计算影响扩散的有效算法。
   然而，由于影响级联模型不同，它们不能直接解决[5]中所研究的级联模型的贪婪算法的效率为9sue的问题。
   2）Leskovec等人提出了一种选择新种子的优化方法，称为“具有成本效益的懒进”(CELF)方案。
   CELF优化利用影响最大化目标的子模块属性，极大地减少了对影响扩散的评估次数。
   他们的实验结果表明，CELF优化在选择种子顶点时可以达到700倍的速度，这是一个非常令人印象深刻的结果。
   然而，我们的实验表明，改进后的算法在一个有几万个顶点的图上仍然需要几个小时的时间来完成，因此对于大规模的网络仍然是不有效的。
7. 在本文中，我们从两个互补的方向来解决影响最大化的效率问题。
   1）我们设计了新的方案来进一步改进贪婪算法，并将我们的方案与CELF优化相结合，得到更快的贪婪算法。
   2）我们提出了新的程度折扣启发式，其影响扩散明显优于经典的程度和基于中心的启发式，并接近贪婪算法的影响扩散。
   3）我们的启发式的最大优势是它们的速度，因为它们比所有贪婪算法快许多个数量级。

我们的新贪婪算法和程度折扣启发式是从独立级联模型和加权因果关系模型推导出来的。
我们在两个真实的协作网络上进行了大量的实验，将我们的算法与CELF优化算法以及经典的度和中心性启发式算法进行比较。
我们比较的两个指标是影响扩散和运行时间。
对于我们的新贪婪算法，它们的影响扩散与原始贪婪算法完全匹配，而运行时间比CELF优化缩短了15% - 34%。
对于我们的程度折扣启发式算法，它们的影响扩散接近于贪婪算法，并始终优于经典的基于程度和基于中心的启发式算法。
针对传播概率较小的独立级联模型优化的一种特殊启启式算法几乎与独立级联模型中贪婪算法的影响扩散(与一个实验图中的贪婪算法相同，在另一个图中较低3.4%)匹配。

改进的贪心算法

对独立级联模型和加权级联模型中贪心算法的改进。

1. 设S为被选中用于启动影响传播的顶点子集，我们称之为种子集。
2. 设RanCas(S)表示从种子集S开始的影响级联的随机过程，其输出是受S影响的随机顶点集。

本文中的算法以图G和一个数字k为输入，生成基数为k的种子集S，目的是使受种子集S影响的顶点的期望数量最大化，即我们所说的影响扩散尽可能大。

1. 算法1描述了给定一个RanCas()运行的dom进程的一般贪婪算法。
   1）在每一轮i中，算法向选定的集合S中添加一个顶点，使该顶点与当前的集合S一起使影响扩展最大化(第10行)。
   2）等价地，这意味着在第i轮中选择的顶点是该轮中增量影响分布最大倍数的顶点。
   3）为此，对于每个顶点v不属于S，用R次ranas (S∪{v})的重复模拟来估计S∪{v}的影响范围(第3-9行)。
   4）每个RanCas(S)的计算需要O(m)时间，因此算法1需要O(knRm)时间来完成。

2. Leskovec等提出了基于影响最大化目标的子模块性的原始贪婪算法的CELF优化。
   1）子模块性是在向种子集S中添加顶点v时，如果S越小，则由于添加v而产生的增量影响扩散越大。
   2）CELF优化利用了子模块性，这样在每一轮中，大量节点的实际影响扩散不需要重新评估，因为它们在前一轮中的值已经小于当前一轮中评估的其他一些节点的值。
   3）CELF优化具有与原始贪婪算法相同的影响传播，但速度要快得多，实际上是700倍。

3. 在本文中，我们将改进的贪婪算法与celf优化的贪婪算法的运行时间进行了比较，表明我们可以进一步改进贪婪算法。
   级联模型(独立级联模型和加权级联模型)之间的主要区别是随机耦合过程RanCas(S)，下面将对此进行解释。

对独立级联模型的改进

GeneralGreedy
RanCas(S)的工作原理如下：

1. 设Ai是第i轮被激活的顶点集合，且初始化时A0 = s。对于任何uv∈E，即u∈Ai但v尚未激活，v在第(i + 1)轮被u激活，具有独立的概率p，我们称之为传播概率。
2. 重复这个过程，直到Ai+1为空.
3. 注意，在随机过程RanCas(S)中，每条边uv只确定一次，从u到v或从v到u，决定影响是否通过这条边传播。
4. 两个方向上的概率都是相同的传播概率p。因此，我们可以先确定uv是否被选择用于传播，并从G中去除所有不用于传播的边，得到一个新的图g0。
5. 随机集RanCas(S)就是g0中从S可达的顶点集合
6. 通过随机生成R次g0，每次对图g0进行线性扫描

在NewGreedyIC【优化一】中，每个随机图都用于估计所有顶点的影响扩散，这可能导致影响扩散估计之间的相关性。
然而,我们相信这些相关性是无关紧要的,因为(a)他们不影响每个顶点的估计,(b)相关性主要是由于生成顶点共存同一连接组件的一些随机图,小比较图的大小,和©估计为平均从大量的随机图(例如R = 20000),因此对于每一对顶点他们只在一小部分共存的随机图采样。
我们的实验结果表明,使用相同的NewGreedyIC达到GeneralGreedy一样的传播影响,所以没有必要增加R补偿相关的效果。

比较NewGreedyIC算法【优化一】和 CELF优化【优化二】，在运行时间上有一个权衡。

1. 在CELF优化中，它的第一轮和原始算法一样慢。
2. 然而，从第二轮开始，每轮可能只需要探索少量顶点，而且每个顶点的探索通常很快，因为RanCas (S)通常在探索图的一小部分后停止。
3. 相反，在NewGreedyIC算法的每一轮中，我们需要遍历整个图R次，以生成R个随机图g0。
4. 为了结合这两种改进的经验，我们进一步考虑 MixGreedyIC【优化三】 算法，在第一轮中我们使用NewGreedyIC来选择第一个种子并计算所有顶点的影响扩散估计，然后在后面的几轮中我们使用CELF优化来选择剩余的种子。

对加权级联模型的改进

1. 设dv是图G中节点v的度，设uv是G中的一条边。
2. 在加权级联(WC)模型中，如果u在第i轮被激活，那么v在第i+ 1轮被u激活的概率为1/dv。
   与IC模型相似，每个邻居都可以独立激活v。
3. 因此，如果一个尚未激活的顶点v在第i轮中有l个邻居被激活，则v在第i + 1轮中被激活的概率为1−(1−1/dv)^l
4. WC模型中的RanCas(S)与IC模型的 主要区别在于，u激活v的概率通常与v激活u的概率不相同。 因此，我们构建了一个有向图G = (v, E)，其中每条边uv∈E都被两个有向边uv和vu所取代。我们仍然用dv来表示原图中v的度
5. 利用与IC模型相同的思想，在贪婪算法的每一轮中，当选择一个新顶点加入到现有的种子集S中时，我们生成R个随机有向图G0
6. 对于每个顶点v和每个图g0，我们要计算|RG0 (S∪{v})|，然后对所有g0求平均值，得到S∪{v}的影响范围，并选择使该值最大化的v。

改进度折扣算法

在影响最大化的种子选择中，常使用度。
选择度最大的顶点作为种子的影响扩散比其他启发式算法更大，但仍然没有贪婪算法产生的影响扩散大。
我们提出了度折扣启发式，它的性能接近于IC模型的贪婪算法。

1.基本折扣思路如下：
设v是顶点u的邻居。
如果u已经被选择为一个种子，那么在考虑根据v的度数选择v作为一个新的种子时，我们不应该对其度数计算vu边。
因此，由于u在种子集中，我们应该对v的度进行减1的折现，并且我们对已经在种子集中的v的每一个邻居进行同样的折现。
这是一个适用于所有级联模型的基本程度折扣启发式，在我们的实验部分称为SingleDiscount。

2.更精确的度折现启发式
因为v是u的邻居，而u被选进了种子集，且至少有p的概率，v会受到u的影响，在这种情况下，我们不需要把v选进种子集。
这就是为什么进一步的折扣更准确的原因。

1. 当p较小时，我们可以忽略v对多跳邻居的间接影响，而只关注v对其近邻的直接影响，使得度折计算易于管理。
2. 记 N(v) = {v}∪ {w ∈ V | vw ∈ E}是v的邻居集合。
3. 设**Star(v)**为以N(v)为顶点，以v为边（N(v）与v的所有边）的子图。
4. 计算节点v对Star(v)的附加影响【创新点】：
   
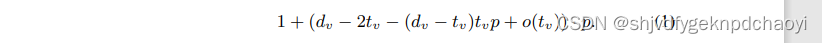
   具有传播概率p的IC模型：
   设tv是顶点v的已经被选为种子的邻居数。
   节点v的度：dv = O(1/p)，tv = o(1/p)