1 组合数计算公式

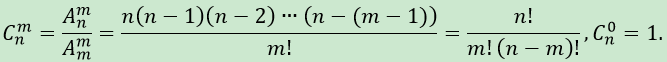
组合公式的推导由排列公式去掉重复的部分得来。

• 排列是，从n个不相同元素中取出m个排成一列（有序），第一个位置可以有n个选择，第二个位置可以有n-1个选择（已经有1个放在前一个位置），则同理可知第三个位置可以有n-2个选择，以此类推第m个位置可以有n-(m-1)个选择，则排列数公式为：
  

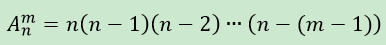
• 组合是，从n个不同的元素中取出m个成为一组（无序），显然，m个元素组成的一组可以有
  
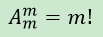
  种不同的排列（全排列）。

所以，每m!个排列中，只有一个组合， 故组合的计算公式就是

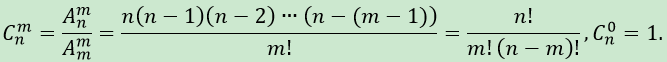
参考文献：
[1]组合数公式_百度百科
[2] 组合数_百度百科

2 最小二乘法

工程上，常常要根据两个变量的多组实验数值，找出这两个变量间的函数关系的近似表达式。

1. 首先，要确定这个近似表达式f(t)的类型：假设近似为线性函数f(t)=at+b。其中a,b为常数。
2. 如何确定常数a，b？
   最理想的情况是使直线f(t)=ax+b经过源数据中的(x,y)各点，但在实际上是不可能的，因为这些点本来就不在同一条直线上。
   因此，只能要求选取这样的a,b使得f(t)=at+b在t0 ~ tn处的函数值与实验数据y0 ~ yn相差都很小，就是要使偏差yi - f(ti) (i=0,1,…,n)都很小。如何达到这一要求呢？能否使偏差的和(y0-f(t0)) +… +(yn-f(tn))很小来保证每个偏差都很小呢？不能，因为偏差有正有负，在求和时，可能互相抵消。为了避免这种情形，可对偏差取绝对值再求和，只要|(y0-f(t0))| +… + |(yn-f(tn))|很小，就可以保证每个偏差的绝对值都很小。但是这个式子中有绝对值记号，不便于进一步分析讨论。由于任何实数的平方都是正数或零，因此可以考虑选取常数a与b，使
   (y0-f(t0)) ^ 2 +… + (yn-f(tn)) ^2最小来保证每个偏差的绝对值都很小。
   这种根据，“偏差的平方和为最小”的条件，来选择常数a与b的方法叫做最小二乘法。

3 sigmoid函数

sigmoid 函数：

其函数图像如下：

可以看出，sigmoid函数连续，光滑，严格单调，以(0,0.5)中心对称，是一个非常良好的阈值函数。

当x趋近负无穷时，y趋近于0；趋近于正无穷时，y趋近于1；x=0时，y=0.5。当然，在x超出[-6,6]的范围后，函数值基本上没有变化，值非常接近，在应用中一般不考虑。

Sigmoid函数的值域范围限制在(0,1)之间，我们知道[0,1]与概率值的范围是相对应的，这样sigmoid函数就能与一个概率分布联系起来了。

Sigmoid函数的导数是其本身的函数，即f′(x)=f(x)(1−f(x))，计算非常方便，也非常节省计算时间。推导过程如下：
根据常用的求导公式，得到：
f′(x)=(−1)(1+e−x)−2(0+(−1)e−x)=e−x(1+e−x)2=e−x1+e−x11+e−x

参考文献：Sigmoid函数 - saltriver的专栏 - CSDN 博客