1. 最长递增子序列

300. 最长递增子序列

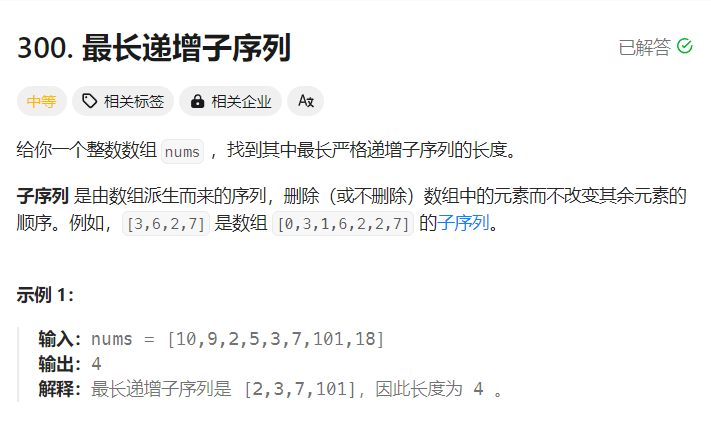
和子数组不同的是，子数组要求是连续的，子序列只要下标是递增的就可以，这里严格递增的意思是不能有相等的元素，必须一直递增

状态表示：以 i 位置为结尾的所有的子序列中最长递增子序列的长度

状态转移方程：

当枚举到 i 位置时，如果是单个 i 构成的子序列那么 dp[i] 就是 1，如果子序列长度大于 1，就是在 0 ~ j （ 0<= j < i）区间内找出一个最长的递增子序列，并且只有在 nums[j] > nums[i] 的时候才能把 d[i] 更新为 dp[j] + 1，由于在 0 ~ j 区间内任意位置都可能有一个最长的递增子序列，所以更新 dp[i] 的时候需要取它们的最大值

初始化：可以吧 dp 表中的元素全部初始化为 1，也就是最差情况都是 1

填表顺序：从左到右

返回值：dp 数组中的最大值

class Solution {public int lengthOfLIS(int[] nums) {int n = nums.length;if(n == 1) return 1;int[] dp = new int[n];Arrays.fill(dp,1);int res = 1;for(int i = 1;i < n;i++){for(int j = 0;j < i;j++){if(nums[j] < nums[i]){dp[i] = Math.max(dp[i],dp[j] + 1);}}res = Math.max(dp[i],res);} return res;}
}

2. 摆动序列

376. 摆动序列

状态表示：由于这道题有上升和下降两种状态，所以可以定义两个状态表示

f[i] ：以 i 位置为结尾的所有子序列中，最后一个状态处于上升状态的最长摆动子序列的长度

g[i] ：以 i 位置为结尾的所有子序列中，最后一个状态处于下降状态的最长摆动子序列的长度

状态表示：

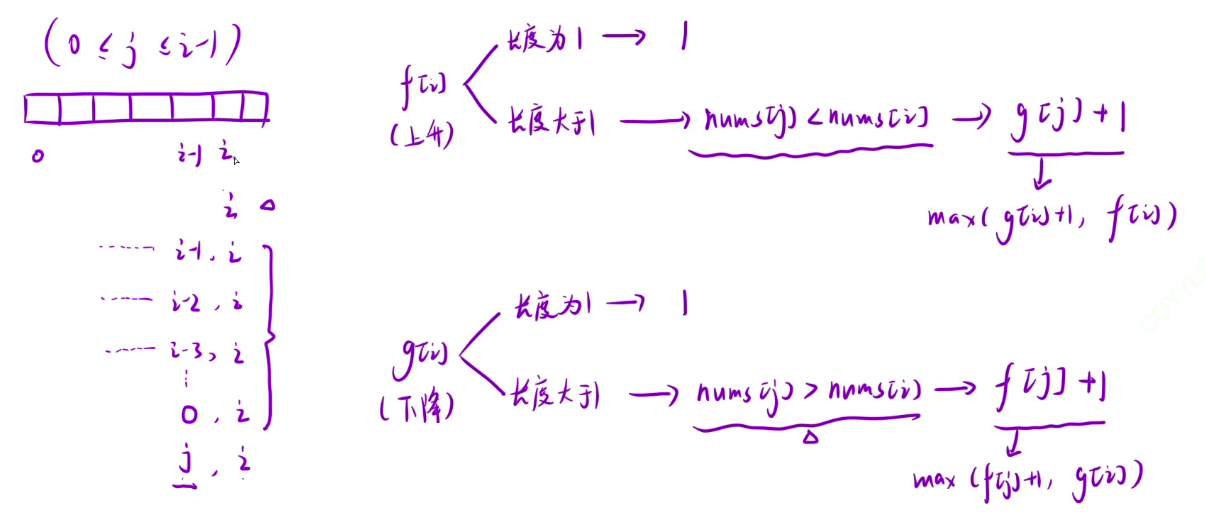
和上一题类似，只不过分为两种情况，当 num[j] < num[i] 时，也就是准备上升的状态，此时 f[i] 就是从 g[j] + 1 中取一个最大值，当 num[j] > num[i] 时，也就是准备下降的状态，此时 g[i] 就是从 f[j] + 1 中取一个最大值

初始化：还是可以把两个 dp 表都初始化为 1

返回值：两个 dp 表中的最大值

class Solution {public int wiggleMaxLength(int[] nums) {int n = nums.length;int[] f = new int[n];int[] g = new int[n];for(int i = 0; i < n;i++){f[i] = g[i] = 1;}int ret = 1;for(int i = 1;i < n;i++){for(int j = 0;j < i;j++){if(nums[i] > nums[j]){f[i] = Math.max(g[j] + 1,f[i]);}if(nums[i] < nums[j]){g[i] = Math.max(f[j] + 1,g[i]);}}ret = Math.max(g[i],ret);ret = Math.max(f[i],ret);}return ret;}
}

3. 最长递增子序列的个数

673. 最长递增子序列的个数

状态表示：

dp[i] 还是像之前一样存储以 i 结尾最长递增子序列的长度，还需要统计个数，所以还需要再定义一个状态来表示以 i 结尾时最长递增子序列的个数

状态转移方程：

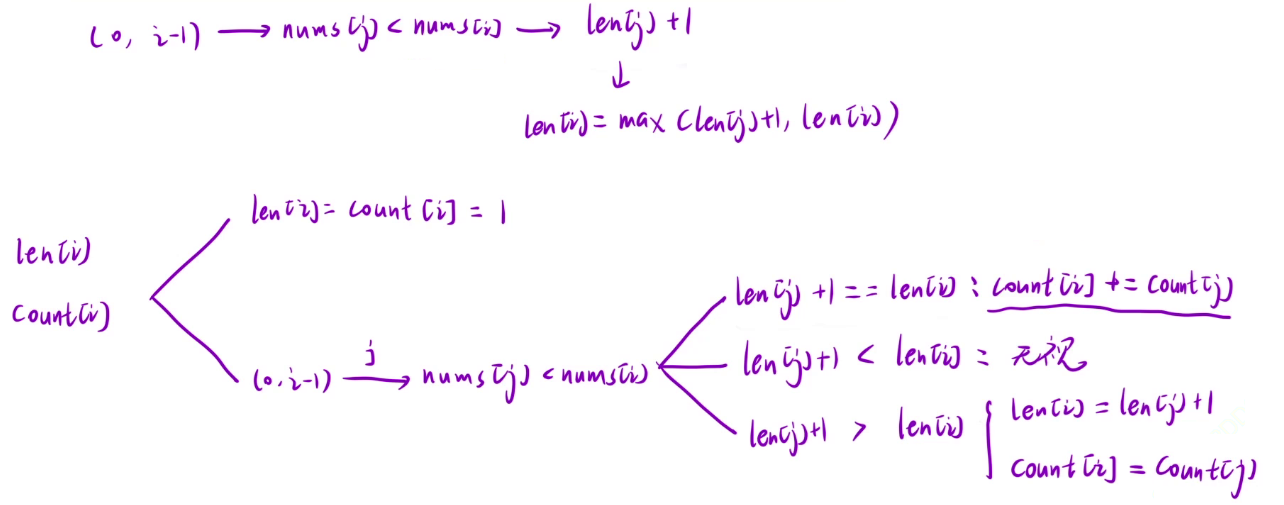
求最长递增子序列的长度是和之前一样的，求个数的时候由于以 i 结尾时可能会有多个递增子序列的长度是一样的，所以就需要把这些情况都加起来，由于求的是最长的子序列，在开始从左往右遍历的时候还不能确定整个数组中的最长递增子序列长度，但是可以知道以当前位置结尾时的最长长度，当后续再遇到更长的子序列，就需要把 count 表里的重新更新，遇到一样的话就相加

两个表都初始化完之后再按照上面的方法遍历一遍求出最长递增子序列的个数即可

class Solution {public int findNumberOfLIS(int[] nums) {int n = nums.length;int[] dp = new int[n];int[] count = new int[n];for(int i = 0;i < n;i++){dp[i] = count[i] = 1;}for(int i = 1;i < n;i++){for(int j = 0;j < i;j++){if(nums[i] > nums[j]){//长度一样if(dp[i] == dp[j] + 1){count[i] += count[j];}//找到了更长的子序列if(dp[i] < dp[j] + 1){count[i] = count[j];dp[i] = dp[j] + 1;}}}}int ans = 0,ret = 1;for(int i = 0;i < n;i++){if(ret < dp[i]){ret = dp[i];ans = count[i];}else if(ret == dp[i]){ans += count[i];}}return ans;}
}

4. 最长数对链

646. 最长数对链

使用动态规划时需要确定之前的状态，但是这道题如果直接进行表示的话，下一个位置选在哪里是不能确定的，所以需要提前排好顺序，然后就变成了最长递增子序列的问题，此时只要 pairs[i][0] 的元素大于上一个 pairs[j][1]，就可以连在上一个状态上了

class Solution {public int findLongestChain(int[][] pairs) {Arrays.sort(pairs,(a,b)->a[0] - b[0]);int n = pairs.length;int[] dp = new int[n];Arrays.fill(dp,1);int ret = 1;for(int i = 1;i < n;i++){for(int j = 0;j < i;j++){if(pairs[i][0] > pairs[j][1]){dp[i] = Math.max(dp[i],dp[j] + 1);}}ret = Math.max(ret,dp[i]);}return ret;}
}