从逻辑回归开始学习神经网络
神经网络直观上解释,就是由许多相互连接的圆圈组成的网络模型:

而逻辑回归可以看作是这个网络中的一个圆圈:

圆圈被称为神经元,整个网络被称为神经网络。
本节的任务是我们究竟如何理解具体的一个神经元,又如何将神经元组成一个大的神经网络。

为了后面的描述更加严谨,这里做一个提前声明,神经网络中所使用的激活函数 f(z) 全部都是 sigmoid 函数。
这样的声明是为了确保每一个神经元都对应一个逻辑回归模型,这个声明此时看不懂不要紧,后面会具体解释。
神经元和神经网络
直接学习神经网络不见得好懂,因此我们先看其中一个具体的圆圈(即神经元,也被称作感知机)是如何工作的:

对于上图这样的一个网络,用红色圆圈标记其中一个神经元,在其前面有三条连接线指向它,在它后面有两条连接线从该神经元发出:

这说明在这个神经元的前面一层中有3个神经元在向这个神经元发送数据,数据经过该神经元的计算,又发送给后面一层的两个神经元。
现在我们明白了这个神经元的前后连接关系,为了后续说明的简单,我们删掉前面的神经元,只保留这个神经元的3条输入线段,对于当前关注的这个红圈的神经元,会给后面的两个神经元发送数据,但只会计算一个结果,因此我们只保留一条连线表示数据从该神经元发送出去:

现在图像就很清楚明了了:

接下来就可以讨论该神经元是如何工作的了。
逻辑回归模型

一个神经元的工作方式就是逻辑回归模型的工作方式,这里不打算从头开始讲逻辑回归,如果只是单纯想看懂本节的内容,甚至不需要知道逻辑回归是干什么的,我们只需要知道逻辑回归是如何计算的就可以了。

前面说的3条连接线,对应了3条输入数据,也就是有3个输入特征,我们用 x1、x2、x3 来表示这3条数据,每一个逻辑回归都有一组参数w和b参数,这个参数就是大家常听到的大模型中的8B、70B的那种参数,只不过8B指的是w和b的总和是80亿,由于这里的逻辑回归只有x123,3个输入特征,因此该回归模型一共有3个w和1个b ,共4个参数。

神经元中的 b 被称为偏置参数,一般不画在模型中,但计算的时候要带上它,在表示神经元的圆圈中写出计算方法,也就是上图中的公式,在经过该公式的计算后得到 z,z 再经过激活函数 f() 后得到输出结果 a 。
这样就得到了逻辑回归模型的结构图。
在计算神经元的输出时,使用的是中学数学中直线方程的计算方法:

但是注意,这里的直线方程是空间中的直线方程,平面与空间中的直线方程差异如下:

对于空间中的直线方程我们可以使用 Σ 求和符号来表示:

因此我们举例的神经元可以计算如下:

最终将 z 输入到激活函数 f 中得到最后的输出 a 。
激活函数 f() :

这里的 f 选择的是 sigmoid 函数,函数图像如上图右侧,通过 sigmoid 函数我们可以将任意实数值映射到 0 和 1 之间:

之前声明说,将激活函数默认设置为是 sigmoid 函数,这样神经网络才是由逻辑回归组成的,这是因为如果抛开逻辑回归只考虑神经网络的神经元的话,那么激活函数可以有很多的选择:

当选择其它的函数作为激活函数时,网络中的神经元就不再是逻辑回归了,本节一直强调逻辑回归是为了让大家了解逻辑回归模型是学习神经网络的基础。
将逻辑回归组成神经网络
最后,我们将一个个的逻辑回归连接到一起就组成了神经网络:

神经网络具有层的概念,例如上图就是一个三层的神经网络,第一层是输入层、第二层是隐藏层、第三层是输出层:

但是对于输入层的神经元不能被看作是逻辑回归,因为它们只是用来接收外界输入的信号的,而隐藏层和输出层中的神经元都可以看作是一个个的逻辑回归模型。
因此上图一共使用了 7 个逻辑回归(隐藏层五个+输出层两个)组成了一个神经网络。
由于神经网络是从前往后计算的,也就是先计算前面层的逻辑回归然后再计算后面层的逻辑回归,因此神经网络的计算被称为是前向传播:

这种神经网络也被称为前馈神经网络。
逻辑回归详解
相信在上面小节中,对于什么是逻辑回归一定非常好奇,这一节就来详解一下逻辑回归。
逻辑回归是应用最为广泛的二分类模型,并且也是进一步学习神经网络等深度学习模型的基础。
本节我们从下面三个角度来详解逻辑回归:
1、什么是线性分类
2、逻辑回归的算法原理
3、PyTorch实现逻辑回归
什么是线性分类
来看下面这个例子:

在平面 x1-0-x2 中,分布着蓝色圆圈表示的正样本,红色叉叉表示的负样本,它们有两个特征 x1 和 x2 .
其中正样本的标签是 y = 1,负样本的标签是 y = 0,然后在平面上画出一条直线:x1 + x2 - 3 = 0
该直线交 x1 轴于点(3, 0) ,交 x2 轴于点(0, 3):

此时可以观察到正负两种样本刚好分布在直线的两侧。
对于任意的某个样本(x1, x2) ,如果将该样本向量带入表达式 x1 + x2 - 3,当计算结果大于等于 0 时那么该样本就是正例,否则就是负例:

这样我们就通过直线 x1 + x2 - 3 = 0,对样本进行了分类,这条直线就是这个分类问题的决策边界。
当使用一条直线来区分样本是正例还是负例,那么这就是线性分类问题。
而逻辑回归算法会训练出一个由直线表示的决策边界,因此逻辑回归是线性分类器。
逻辑回归的算法原理
逻辑回归的假设函数
任何机器学习模型都需要一个假设函数,我们通过假设函数来表示输入数据与输出结果之间的关系。
也就是将样本的特征向量 x ,输入到假设函数中 Hθ(x) 中,计算出模型的预测结果:

逻辑回归的假设函数如下所示:

下面我们就基于分类问题本身,来解释逻辑回归的假设函数 Hθ(x) 。
设平面上的样本正例的标记为 y=1,负例的标记 y=0,那么逻辑回归模型需要预测样本的标记值:预测未知的样本 x 是0还是1。
也就是将未知样本 x 输入到逻辑回归模型,然后模型预测该样本是0还是1。
实际上,我们希望模型的预测结果也就是 Hθ(x) 的输出是 0 到 1 中间的某个值,这样就可以将预测结果 h 看作是样本 x 属于某个类别的概率了。也就是当我们发现预测 h 接近 1 时,样本 x 就更可能是正例,h接近0时,样本 x 更可能是负例。

具体来说,在使用逻辑回归预测样本的类别时,会提前设置一个阈值 p 用来控制分类的界限:

比如阈值 p 设置为 0.5 的话,假设预测值Hθ(x) = 0.75,那么 0.75 >= 0.5 ,因此 x 为正例。
因此基于这样的考虑,为了使得 Hθ(x) 的输出是 0 到 1 区间中的某个值,我们引入 sigmoid 函数,设 sigmoid 函数为 g(z),那么其为下图右侧的公式:

观察 sigmoid 函数会发现,自变量 z 的范围是负无穷到正无穷,z 趋近于负无穷时函数值接近于0,z 趋近于正无穷时,函数值趋近于 1:

并且该函数在 z=0 的位置左右对称。
任意直线的表达式为:

我们将该表达式用 z 表示,并带入到 sigmoid 函数中:

此时就得到了自变量是 x1 到 xn,参数是 θ0 到 θn,值域是 0 到 1 的函数 Hθ(x) 。
该函数就是逻辑回归的假设函数,它由直线 z 和 sigmoid 函数两部分组成。
逻辑回归的代价函数
机器学习模型的代价函数衡量了模型在训练集上所犯的错误大小,因此需要准确的描述样本预测值与真实值之间的误差。
在逻辑回归中,使用交叉熵损失函数作为模型的代价函数:

我们要求出代价函数 J 取得最小值时,逻辑回归模型中的参数 θ0 到 θn 它们的具体值是多少。
下面我们具体来说明为什么逻辑回归的代价函数是交叉熵损失误差:
设下面的公式是某一个样本的代价:

J(θ) 为 m 个样本的平均代价:

在 cost 函数中,Hθ(x)表示样本属于某一个类别的预测概率,y表示样本的标签,cost函数描述了模型对于一个样本所犯错误的大小:

我们希望一个样本的代价 cost,有如下性质:



为了实现拥有这样性质的 cost 函数,我们引入 log 函数,我们将 -log(x) 和 -log(1-x) 两个函数画在坐标系中,这两个函数以 x = 0.5 左右对称,接着将自变量 x 的值限制在 0 到 1 之间:

观察函数图像可以发现,蓝色函数在 x 趋近于 0 时函数值趋近于正无穷,x=1时蓝色函数值为 0.
橙色函数则正好相反。
因此如果函数的自变量 x 就对应模型的预测值 h,那么蓝色函数就恰好可以代表样本为正例时代价 cost 随预测值 h 的变化。
橙色函数则可以表示样本为负例时,代价 cost 随预测值 h 的变化:

基于这样的考虑,就可以设计出如下的 cost 函数:

将上图中的两个函数合成一个,也就是用 Hθ(x)、y 和 log 函数同时表达一个样本的代价值 cost:

最后将 m 个样本的代价值相加到一起除以 m,就得到了逻辑回归的总代价函数 J(θ):

J(θ) 即为我们的交叉熵损失误差。
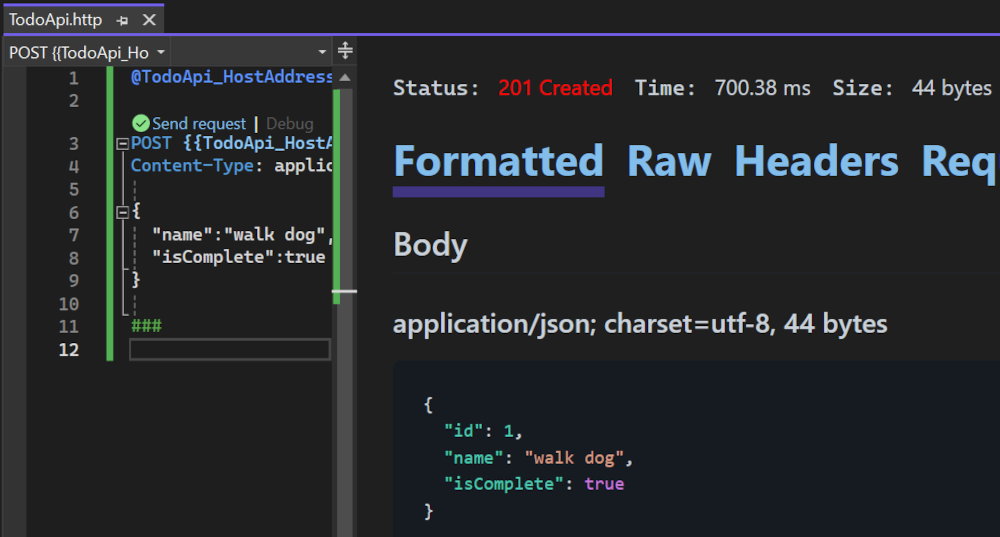
PyTorch实现逻辑回归
接下来我们使用深度学习框架来训练逻辑回归模型。
首先我们要清楚我们要构建的场景类似如下,也就是我们刚刚一直在说的例子:

因此我们可以写出如下代码:
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy
import torch# 实现逻辑回归的假设函数hθ(x) 的计算方法
# 计算逻辑回归模型的预测值hθ(x)
def hypothesis(theta0, theta1, theta2, x1, x2):z = theta0 + theta1 * x1 + theta2 * x2h = torch.sigmoid(z)return h.view(-1, 1)# 实现逻辑回归的代价函数J(θ)的计算方法
# 计算预测值h与真实值y的交叉熵损失函数
def J(h, y):return -torch.mean(y * torch.log(h) + (1 - y) * torch.log(1 - h))if __name__ == '__main__':# 使用mak_blobs函数,在平面上随机生成50个随机样本,包含两个类别x, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.5)# x1, x2分别保存样本的两个特征x1 = x[:, 0]x2 = x[:, 1]# 使用plt.scatter绘制正样本和负样本# 其中正样本使用蓝色圆圈表示,负样本使用红色叉叉表示plt.scatter(x1[y == 1], x2[y == 1], color='blue', marker='o')plt.scatter(x1[y == 0], x2[y == 0], color='red', marker='x')# 将两个特征x1、x2和标签y,转为张量形式x1 = torch.tensor(x1, dtype=torch.float32)x2 = torch.tensor(x2, dtype=torch.float32)y = torch.tensor(y, dtype=torch.float32).view(-1, 1)# 定义直线的3个参数,θ0、θ1、θ2θ0 = torch.tensor(0.0, requires_grad=True)θ1 = torch.tensor(0.0, requires_grad=True)θ2 = torch.tensor(0.0, requires_grad=True)# 定义Adam优化器optimizer,优化三个θ参数optimizer = torch.optim.Adam([θ0, θ1, θ2])for epoch in range(10000): # 进入逻辑回归模型的训练迭代# 计算模型的预测值h = hypothesis(θ0, θ1, θ2, x1, x2)# 调用函数J,计算预测值h与真实值y之间的损失lossloss = J(h, y)loss.backward() # 计算loss关于参数θ的梯度optimizer.step() # 更新模型参数optimizer.zero_grad() # 将梯度清零if epoch % 1000 == 0:# 每一千次迭代打印一次当前的损失,loss.item()是损失的标量值print(f'After {epoch} iterations, the loss is {loss.item():.3f}')# 完成训练后,再基于迭代出的参数,绘制出逻辑回归的蓝色决策边界w1 = θ1.item()w2 = θ2.item()b = θ0.item()x = numpy.linspace(-1, 6, 100)d = -(w1 * x + b) * 1.0 / w2plt.plot(x, d)plt.show()
代码运行输出如下:


可以看到分类效果是不错的。
相信经过上面这一连串的流程讲解,逻辑回归与神经网络应该已经很容易明白了。
补充:逻辑回归与线性回归的区别