深度学习笔记9-实现逻辑回归

Python实现逻辑回归

1.假设函数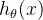 $h_{\theta}(x)$

import math
#sigmoid函数得计算
def sigmoid(z):return 1.0/(1+math.exp(-z))
#逻辑回归假设函数的计算
#函数传入参数theta、样本特征向量x和特征值得个数n
def hypothesis(theta,x,n):h=0.0#保存预测结果for i in range(0,n+1):#将theta-i和xi得乘积累加到h中h+=theta[i]*x[i]return sigmoid(h)#返回sigmoid函数的计算结果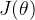

$h_{\theta}(x)=\frac{1}{1+e^{-(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n})}}$

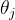2. $J(\theta)$ 关于 $\theta_{j}$ 的偏导数

#J(θ)关于theta-j的偏导数计算
#函数传入样本特征矩阵x和标记y,特征的参数列表theta,特征数n
#样本数量m和待求偏导数的参数下标j
def gradient_thetaj(x,y,theta,n,m,j):sum=0.0#保存sigma求和累加结果for i in range(0,m):#遍历m个样本h=hypothesis(theta,x[i],n)#求出样本的预测值#计算预测值和真实值的差，再乘以第i个样本的第j个特征值x[i][j]#将结果累加到sumsum+=(h-y[i])*x[i][j]

$\frac{\partial J}{\partial \theta_{j}}=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)}$

3.梯度下降迭代

#梯度下降的迭代函数
#函数传入样本的特征矩阵x和样本标签y，特征数n,样本数量m
#迭代速率alpha和迭代次数iterate
def gradient_descent(x,y,n,m,alpha,iterate):theta=[0]*(n+1)#初始化参数列表theta,长的为n+1for i in range(0,iterate):#梯度下降的迭代循环temp=[0]*(n+1)#使用变量j，同时对theta0-thetan这n+1个参数进行更新#同时更新θ参数for j in range(0,n+1):#通过临时变量列表temp，先保存一次梯度下降后的结果#在迭代的过程中调用theta-j的偏导数计算temp[j]=theta[j]-alpha*gradient_thetaj(x,y,theta,n,m,j)#将列表temp重新赋值给列表thetafor j in range(0,n+1):theta[j]=temp[j]return theta#返回参数列表theta

4.代价函数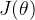 $J(\theta)$

#实现代价函数J(θ)的计算函数costJ
#在迭代时不会使用这个函数，该函数只用于调试
#函数传入样本的矩阵特征x和标签y，参数列表theta,特征个数n和样本个数m
def costJ(x,y,theta,n,m):sum=0.0#定义累加结果for i in range(0,m):#遍历每个样本h=hypothesis(theta,x[i],n)#将样本的预测值与真实值差的平方累加到sum中sum+=-y[i]*math.log(h)-(1-y[i])*math.log(1-h)return sum/m#返回sum/m

$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)})]$

逻辑回归的可视化实验

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as npif __name__ == '__main__':# 使用make_blobs随机的生成正例和负例，其中n_samples代表样本的数量，设置为50# centers代表聚类中心点的个数，可以理解为类别标签的数量，设置为2# random_state是随机种子，将其固定为0，这样每次运行就生成相同的数据# cluster s-t-d是每个类别中样本的方差，方差越大说明样本越离散，这里设置为0.5X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.5)posx1, posx2 = X[y == 1][:, 0], X[y == 1][:, 1]negx1, negx2 = X[y == 0][:, 0], X[y == 0][:, 1]# 创建画板对象，并设置坐标轴board = plt.figure()axis = board.add_subplot(1, 1, 1)# 横轴和纵轴分别对应x1和x2两个特征，长度-1到6axis.set(xlim=[-1, 6],ylim=[-1, 6],title='Logistic Regression',xlabel='x1',ylabel='x2')# 画出正例和负例，蓝色表示正例，红色表示负例plt.scatter(posx1, posx2, color='blue', marker='o', label='Positive')plt.scatter(negx1, negx2, color='red', marker='x', label='Negative')# 完成样本绘制后，进行模型迭代m = len(X)  # 保存样本个数n = 2  # 保存特征个数alpha = 0.001  # 迭代速率iterate = 20000  # 迭代次数# 将生成的特征向量X,添加一列1，作为偏移特征X = np.insert(X, 0, values=[1] * m, axis=1).tolist()y = y.tolist()# 调用梯度下降算法，迭代出决策边界，并计算代价值theta = gradient_descent(X, y, n, m, alpha, iterate)costJ = costJ(X, y, theta, n, m)for i in range(0, len(theta)):print("theta[%d]=%lf" % (i, theta[i]))print('Coast J is %lf' % (costJ))# 根据迭代的模型参数θ，绘制分类的决策边界# 其中θ1、θ2、θ0，分别对应直线中的w1、w2和bw1, w2, b = theta[1], theta[2], theta[0]# 使用linspace在-1到5之间构建间隔相同的100个点x = np.linspace(-1, 6, 100)# 将这100个点，带入到决策边界中，计算纵坐标d = -(w1 * x + b) * 1.0 / w2plt.plot(x, d, color='green', label='Decision Boundary')# 绘制分类的决策边界plt.plot(x, d)plt.legend()plt.show()

部分解释：

1.random_state=0 是 make_blobs 函数中的一个参数，用于控制随机数生成器的种子。具体来说，它的作用如下：

1. 可重现性

控制随机性：在使用随机数生成算法时，每次运行代码可能会生成不同的结果。通过设置 random_state，你可以固定随机数生成器的状态，从而确保每次运行时生成的样本数据相同。
方便调试和测试：在调试模型或测试算法时，能够生成相同的数据集可以帮助你比较不同模型或算法的效果，确保结果的一致性。

2. 参数的取值

random_state 可以是一个整数、None，或者一个随机数生成器对象。如果设置为整数，例如 random_state=0，则会生成确定的随机数序列。如果设置为 None，则每次运行时都会生成不同的随机序列。

代码解释：
posx1, posx2 = X[y == 1][:, 0], X[y == 1][:, 1]
negx1, negx2 = X[y == 0][:, 0], X[y == 0][:, 1] 
X：这是一个包含样本特征的数组，通常是一个二维数组，其中每一行代表一个样本，每一列代表一个特征。

y：这是一个包含样本标签的数组，通常是一个一维数组，标签值为0或1，分别代表负类和正类。

提取正类样本：

X[y == 1]：使用布尔索引提取标签为1的所有样本特征。结果是一个包含所有正类样本的数组。
[:, 0]：从正类样本中提取第一列特征（通常是 x1）。
[:, 1]：从正类样本中提取第二列特征（通常是 x2）。
最终，posx1 和 posx2 分别存储正类样本的第一和第二个特征。

提取负类样本：

X[y == 0]：使用布尔索引提取标签为0的所有样本特征。
[:, 0]：提取负类样本的第一列特征（x1）。
[:, 1]：提取负类样本的第二列特征（x2）。
最终，negx1 和 negx2 分别存储负类样本的第一和第二个特征。

在逻辑回归中，决策边界是通过将模型的假设函数（sigmoid 函数的输出）设置为 0.5 来确定的。对于线性模型，决策边界可以表示为一个线性方程。

假设函数等于 0.5,根据 sigmoid 函数的定义,当 h(x)=0.5 时，z=0。可以写出 $\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}=0$ ,即 $b+w_{1}x_{1}+w_{2}x_{2}=0$ ，因此 $x_{2}=\frac{-(w_{1}*x_{1}+b)}{w_{2}}$

theta[0]=0.769567
theta[1]=1.893082
theta[2]=-1.580095
Coast J is 0.058178

Pytorch实现逻辑回归

1.逻辑回归模型的设计

设计成功后，设置测试，打印模型结构和参数

import torch#基于模型结构，实现逻辑回归模型
#定义类Logistic Regression,继承nn.Module类
class LogisticRegression(torch.nn.Module):#init函数用于初始化模型#函数传入参数n，代表输入特征的数量def __init__(self,n):super(LogisticRegression,self).__init__()#定义一个线性层，该线性层输入n个特征，输出1个结果self.layer = torch.nn.Linear(n,1)#forward函数用于定义模型前向传播的计算逻辑#函数出入数据xdef forward(self,x):z=self.layer(x)#将x输入至线性层#将结果z输入至sigmoid函数，计算逻辑回归的输出h=torch.sigmoid(z)return h#返回结果h
#在main函数中实现模型的测试代码
if __name__ == '__main__':#创建模型model,输入特征的个数为3model=LogisticRegression(3)print(model)#打印model看到模型的结构print('')#使用循环，遍历模型中的参数for name,param in model.named_parameters():#打印参数名name和参数的尺寸param.data.shapeprint(f'{name}:{param.data.shape}')print()#定义一个100*3大小的张量，代表了100个输入数据，每个数据包括3个特征值x=torch.randn(100,3)h=model(x)#将x输入至模型model，得到预测值hprint(f'x:{x.shape}')

2.生成数据并进行预处理

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as npif __name__=='__main__':X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.5)posx1, posx2 = X[y == 1][:, 0], X[y == 1][:, 1]negx1, negx2 = X[y == 0][:, 0], X[y == 0][:, 1]board = plt.figure()axis = board.add_subplot(1, 1, 1)axis.set(xlim=[-1, 6],ylim=[-1, 6],title='Logistic Regression',xlabel='x1',ylabel='x2')plt.scatter(posx1, posx2, color='blue', marker='o', label='Positive')plt.scatter(negx1, negx2, color='red', marker='x', label='Negative')#将数据转化为tensor张量X=torch.tensor(X,dtype=torch.float32)#view(-1,-1)会将y从1乘以50的行向量转50*1的列向量y=torch.tensor(y,dtype=torch.float32).view(-1,1)model=LogisticRegression(2)#创建逻辑回归模型实例criterion=torch.nn.BCELoss()#二分类交叉熵损失函数#SGD优化器optimizeroptimizer=torch.optim.SGD(model.parameters(),lr=0.001)

3. 模型训练

 for epoch in range(20000):#进入逻辑回归模型的迭代循环#循环迭代的轮数为2万#pytorch框架训练模型的定式：h=model(X)#计算模型的预测值loss=criterion(h,y)#计算预测值h和标签y之间的损失函数loss.backward()#使用backward计算梯度optimizer.step()#使用optimizer.step更新参数optimizer.zero_grad()#将梯度清零if epoch%1000==0:print(f'epoch:{epoch+1} iterations,the loss is {loss.item()}')

4.获取模型参数并绘制决策边界

 #获取model中的模型参数w1=model.layer.weight[0][0].detach().numpy()w2=model.layer.weight[0][1].detach().numpy()b=model.layer.bias[0].detach().numpy()#基于这些参数，绘制决策边界x=np.linspace(-1,6,100)d=-(w1*x+b)/w2plt.plot(x,d,color='blue',label='Decision Boundary')plt.legend()plt.show()