1. 红黑树(RBTree)
为什么HashMap不直接使用AVL树,而是选择了红黑树呢?
由于AVL树必须保证左右子树平衡,Max(最大树高-最小树高) <= 1,所以在插入的时候很容易出现不平衡的情况,一旦这样,就需要进行旋转以求达到平衡。正是由于这种严格的平衡条件,导致AVL需要花大量时间在调整上,故AVL树一般使用场景在于查询场景, 而不是 增加删除 频繁的场景。
红黑树(rbt)做了什么优化呢?
红黑树(rbt)继承了AVL可自平衡的优点,同时, 红黑树(rbt)在查询速率和平衡调整中寻找平衡,放宽了树的平衡条件,从而可以用于增加删除 频繁的场景。在实际应用中,红黑树的使用要多得多。
与AVL树相比,红黑树牺牲了部分平衡性,以换取插入/删除操作时较少的旋转操作,整体来说性能要优于AVL树。虽然RBTree是复杂的, 但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的:
1.1 红黑树的特性(5条原则)
口诀:根黑叶黑,非红即黑,红黑相连,黑数相等
- 节点非黑即红
- 根节点一定是黑色
- 叶子节点(nil)一定是黑色
- 每个红色节点的两个子节点都为黑色。(等价于每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径,都包含相同数目的黑色节点。
RBT有点属于一种空间换时间类型的优化,
在avl的节点上,增加了 颜色属性的 数据,相当于 增加了空间的消耗。 通过颜色属性的增加, 换取,后面平衡操作的次数 减少。
- 红色属性 说明,红色节点的孩子,一定是黑色。 但是,RBTree 黑色节点的孩子,可以是红色,也可以是黑色。
- 叶子属性 说明, 叶子节点可以是空nil ,AVL的叶子节点不是空的,具体如下图。

基于上面的原则,我们一般在插入红黑树节点的时候,会将这个节点设置为红色,
原因参照最后一条原则: 红色破坏原则的可能性最小,如果是黑色, 很可能导致这条支路的黑色节点比其它支路的要多1,破坏了平衡。
1.2 黑色完美平衡
红黑树并不是一颗AVL平衡二叉搜索树,从图上可以看到,根节点P的左子树显然比右子树高
根据 红黑树的特性5,从任一节点到其每个叶子的所有路径,都包含相同数目的黑色节点, 说明:
rbt 的 左子树和右子树的黑节点的层数是相等的
红黑树的平衡条件,不是以整体的高度来约束的,而是以黑色节点的高度,来约束的。

去掉 rbt中的红色节点,会得到 一个四叉树, 从根节点到每一个叶子,高度相同,就是rbt的root到叶子的黑色路径长度。
1.3 红黑树的恢复平衡过程的三个操作
一旦红黑树5个原则有不满足的情况,我们视为平衡被打破,如何恢复平衡?
1.3.1 变色
节点的颜色由红变黑或由黑变红。(这个操作很好了解)
1.3.2 左旋
以某个结点作为支点(pivot),其父节点(子树的root)旋转为自己的左子树(左旋),pivot的原左子树变成 原root节点的 右子树,pivot的原右子树保持不变。

1.3.3 右旋
以某个结点作为支点(pivot),其父节点(子树的root)旋转为自己的右子树(右旋),pivot的原右子树变成 原root节点的 左子树,pivot的原左子树保持不变。

2. 红黑树插入节点情况分析
默认新插入的节点为红色,因为父节点为黑色的概率较大,插入新节点为红色,可以避免颜色冲突。
2.1 红黑树为空树
直接把插入结点作为根节点就可以了。
另外:根据红黑树性质 2根节点是黑色的。还需要把插入节点设置为黑色。
2.2 插入节点的Key已经存在
更新当前节点的值,为插入节点的值。

2.3 插入节点的父节点为黑色
由于插入的节点是红色的,当插入节点的父节点是黑色时,不会影响红黑树的平衡,所以: 直接插入无需做自平衡(因为每个节点自带两个Nil黑色节点)。

2.4 插入节点的父节点为红色
根据性质2:根节点是黑色。
如果插入节点的父节点为红色节点,那么该父节点不可能为根节点,所以插入节点总是存在祖父节点(三代关系)。
根据性质4:每个红色节点的两个子节点一定是黑色的。不能有两个红色节点相连。
此时会出现两种状态:
- 父亲和叔叔为红色
- 父亲为红色,叔叔为黑色

2.4.1 父亲和叔叔为红色节点
根据性质4:红色节点不能相连 ==》祖父节点肯定为黑色节点:
父亲为红色,那么此时该插入子树的红黑树层数的情况是:黑红红。
因为不可能同时存在两个相连的红色节点,需要进行 变色, 显然处理方式是把其改为:红黑红
变色处理:黑红红 ==> 红黑红
- 将F和V节点改为黑色
- 将P改为红色
- 将P设置为当前节点,进行后续处理

可以看到,将P设置为红色了,如果P的父节点是黑色,那么无需做处理;
但如果P的父节点是红色,则违反红黑树性质了,所以需要将P设置为当前节点,继续插入操作, 做自平衡处理,直到整体平衡为止。
2.4.2 叔叔为黑色,父亲为红色,并且父亲节点是祖父节点的左子节点

2.4.2.1 插在父亲的左节点(LL型失衡)
细分场景 1: 新插入节点,为其父节点的左子节点(LL红色情况), 插入后 就是LL 型失衡

- 变颜色:将F设置为黑色,将P设置为红色
- 对F节点进行右旋

2.4.2.2 插在父亲的右节点(LR型失衡)
细分场景 2: 新插入节点,为其父节点的右子节点(LR红色情况), 插入后 就是LR 型失衡

- 对F进行左旋
- 将F设置为当前节点,得到LL红色情况
- 按照LL红色情况处理(1.变色 2.右旋P节点)

2.4.3 叔叔为黑节点,父亲为红色,并且父亲节点是祖父节点的右子节点

2.4.3.1 RR型失衡
新插入节点,为其父节点的右子节点(RR红色情况)

自平衡处理:
1.变色:将F设置为黑色,将P设置为红色
2.对P节点进行左旋

2.4.3.2 RL型失衡
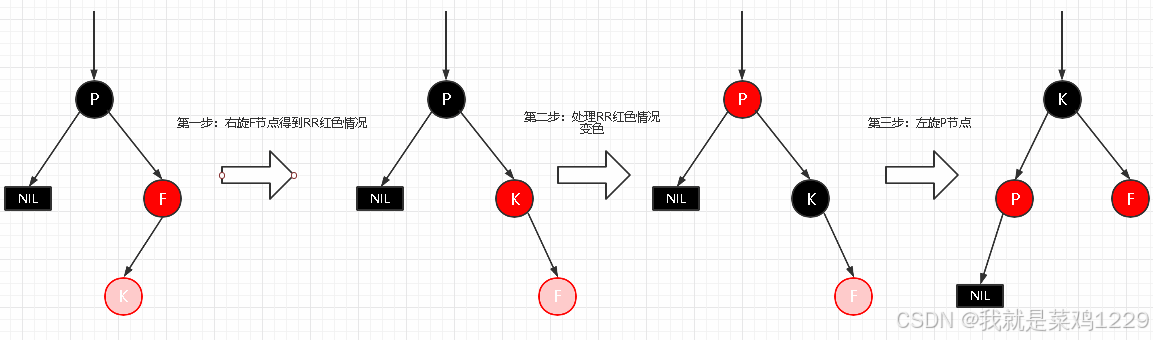
新插入节点,为其父节点的左子节点(RL红色情况)

自平衡处理:
- 对F进行右旋
- 将F设置为当前节点,得到RR红色情况
- 按照RR红色情况处理(1.变色 2.左旋 P节点)