目录
引言：
什么是鸡尾酒排序（CocktailShaker_sort）？
鸡尾酒排序的排序原理：
鸡尾酒排序的过程演示：
Step 1 ：
Step 2 ：
Step 3 ：
Step 4 ：
Step 5 ：
Step 6 ：
Step 7 ：
Step 8 ：
step 9（跳出循环） ：
程序代码（C）：
程序验证：
对鸡尾酒排序的思考和优化：
对鸡尾酒排序的总结：
引言：
鸡尾酒排序是我在算法可视化视频里接触到的一个算法，我发现鸡尾酒排序的算法在排序效率上是优于冒泡排序的，在写鸡尾酒算法的代码之前，我们先对鸡尾酒排序的排序过程和排序原理做一下简单梳理。
什么是鸡尾酒排序（CocktailShaker_sort）？
鸡尾酒排序就是双向冒泡排序，也叫搅拌排序、涟漪排序。我们知道冒泡排序本质上是利用下标对序列中不符合前小后大的两个元素进行交换并循环此过程直到将序列中所有的元素排序完成，在整个排序的过程中，冒泡排序的每一次过程都是从下标为0的第一个元素开始进行排序操作，那么如果我们像折半查找那样定义左边界和右边界，每次排序都在左边界和右边界中轮流进行，结束每次的排序过程后左边界和右边界均缩进一位，直到整个序列排序完成，这样是不是就比单向的冒泡排序的效率提高了很多。
鸡尾酒排序的排序原理：
本质上就是双向或对向的冒泡排序，第一趟是从左边界开始遍历，第二趟开始从右边界开始遍历，每趟完成后边界进行缩进，每趟轮流着进行，直到排序完成。
鸡尾酒排序的过程演示：
例如在这里我给出10个数，分别是：9，15，10，23，6，22，11，12，28，我们就用这9个数来演示鸡尾酒排序的过程：
Step 1 ：
定义左边界left和右边界right和下标 i 和 j ，使这两个下标分别对right边界和left边界：
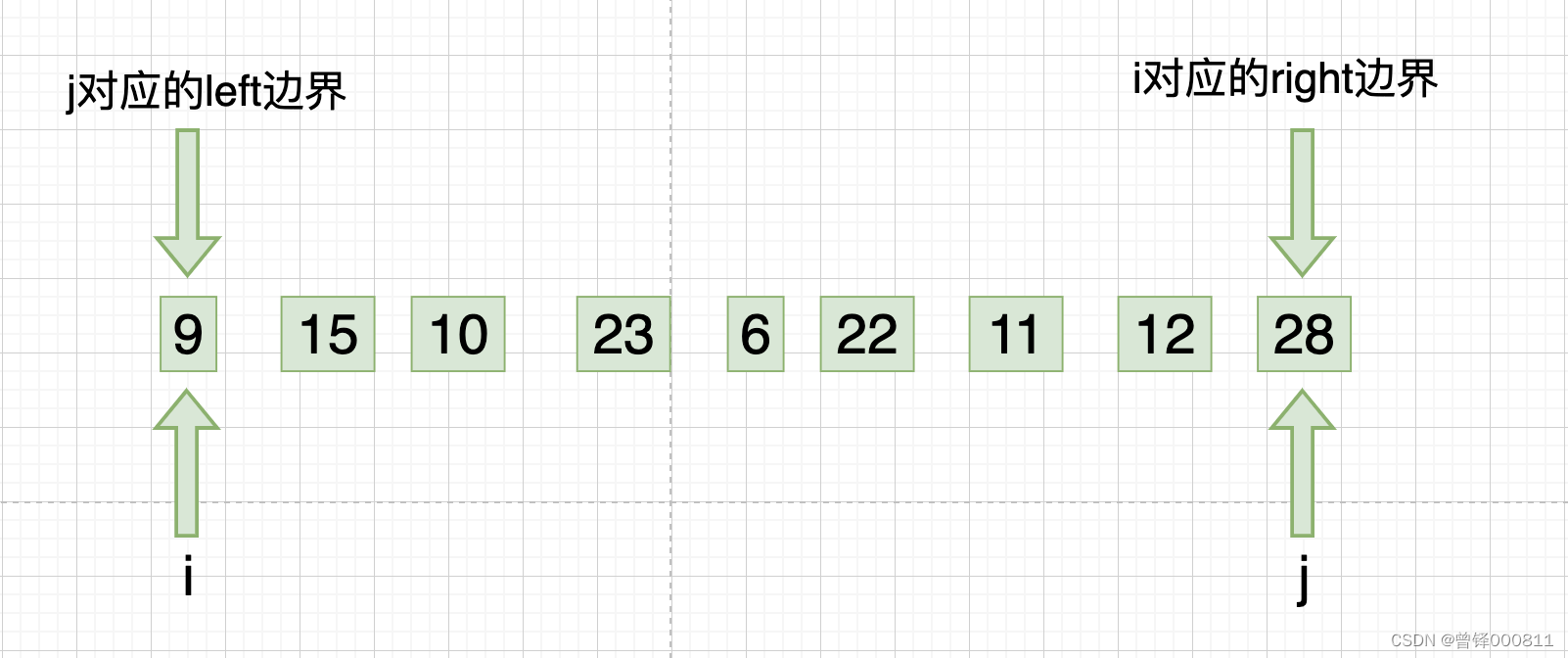
Step 2 ：
此时i下标对序列进行从左向右的第一次遍历，我们使用冒泡排序的规则对序列进行第一次排序，我们将15和10的位置进行调换，将23和6进行交换，交换后我们发现23 大于 22、11、12，调换位置，第二趟位置调换完成之后，i下标对应的right边界向左缩进一位，如下：
Step 3 ：
此时i下标回归left边界，j下标开始从右向左的第一次遍历，我们将11、22的位置进行调换，6也小于15、10、9，所以将6进行位置调换，第三趟调换完成之后，将j对应的left边界向右缩进一位，如图：
Step 4 ：
此时，j下标回归right边界，i下标开始从左向右的第二次遍历，此时将10、15、11、22、12进行位置调换，调换完成之后i下标对应的right边界向左缩进一位：
Step 5 ：
此时i下标回归left边界，j下标开始从右向左的第二次遍历，我们将12、15元素进行调换，调换完成后，j下标对应的left边界向右缩进一位，如图：
Step 6 ：
此时j下标回归right边界，i下标开始从左向右的第三次遍历，我们发现10、11、12、15都是符合升序规则的，此时i下标对应的right边界向左缩进一位，如图：
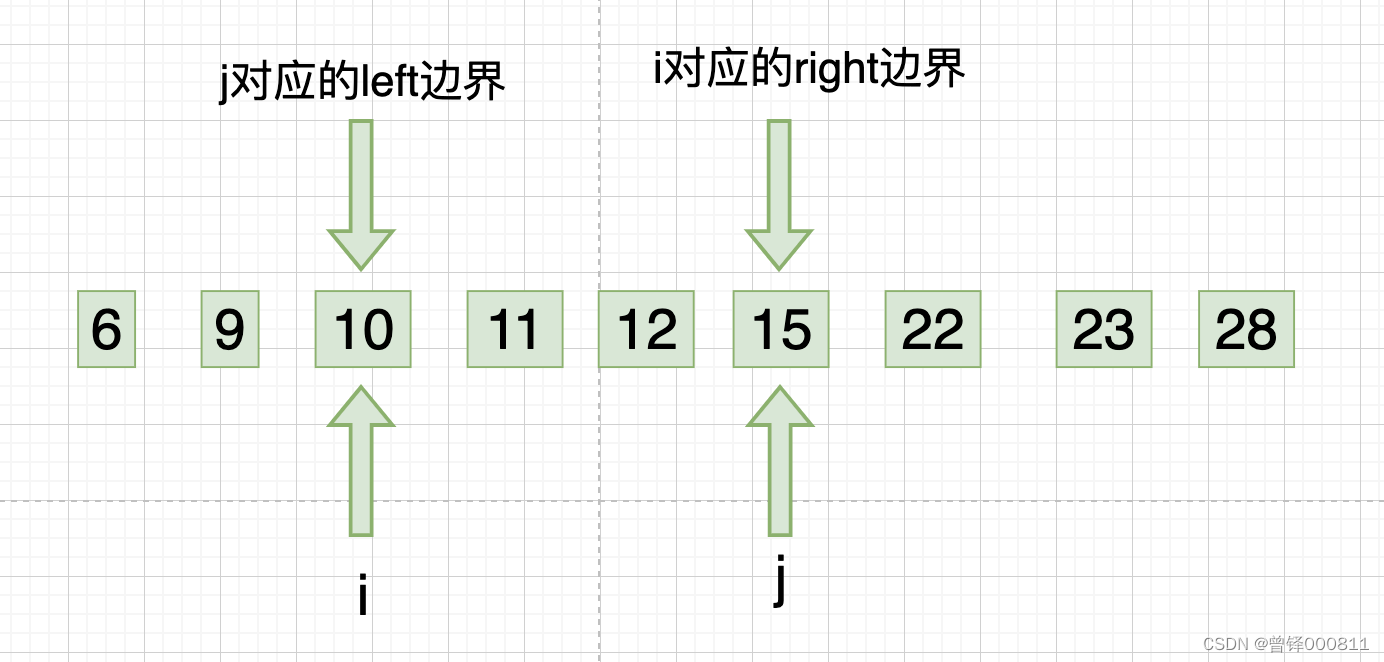
Step 7 ：
此时i下标回归left边界，j下标开始从右向左的第三次遍历，我们发现15、12、11均符合升序规则，则此时j下标对应的left边界向右缩进一位，如图：
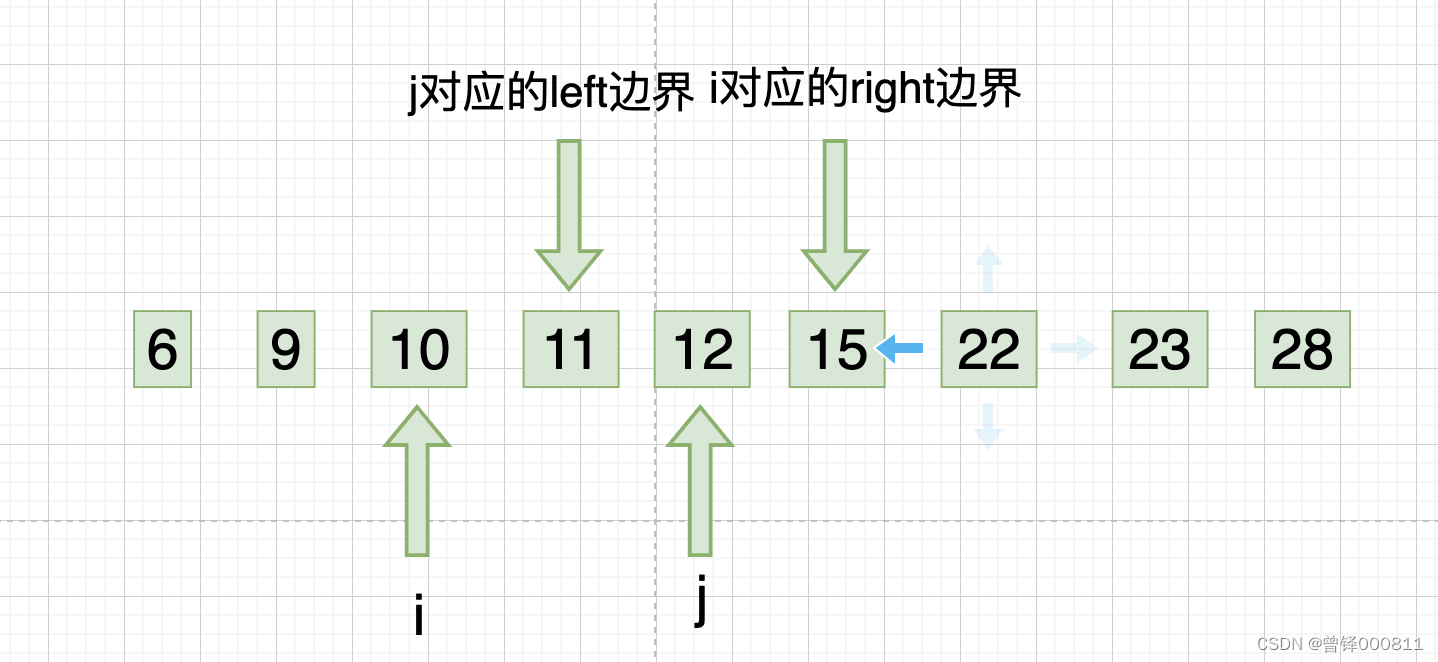
Step 8 ：
此时j下标回归right边界，i下标开始从左向右的第四次遍历，我们发现12、15均符合升序规则，则此时i下标对应的right边界向左缩进一位，如图：
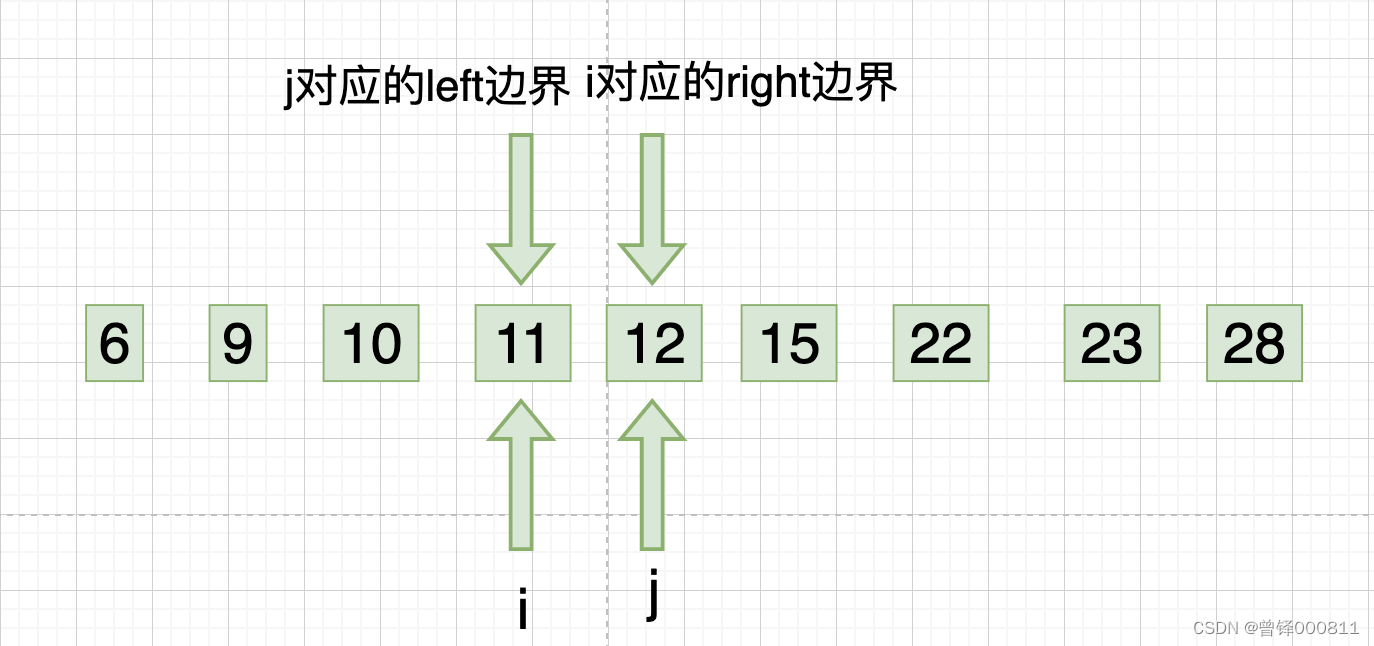
step 9（跳出循环） ：
此时i下标回归left边界，j下标开始从右向左的第五次遍历，我们发现只剩下一个元素12，此时本应该j下标对应的left边界向右缩进一位，但是这时如果进行缩进操作，就不满足left边界小于right边界的设定，此时我们跳出循环，现在的序列顺序就是排列好的升序顺序：
程序代码（C）：
#include<stdio.h>
#include<iostream>
#include<stdlib.h>
#include<assert.h>
#include<time.h>
#define MAXSIZE 10
void initar(int *ar,int len)//初始化数组
{assert(ar != nullptr);for(int i = 0;i < len;i++){ar[i] = rand() % 30;}
}
void showar(int *ar,int len)//打印数组
{assert(ar != nullptr);for(int i = 0;i < len;i++){printf("%d ",ar[i]);}printf("\n--------------------------\n");
}
void swap(int *ar,int index1,int index2)//交换函数
{int temp = ar[index1];ar[index1] = ar[index2];ar[index2] = temp;
}
void Cocktail_sort(int *ar,int len)//鸡尾酒排序
{assert(ar != nullptr);int left = 0;//定义左边界int right = len - 1;//由于使用的是下标，所以右边界为长度减一while(left < right){//大循环条件为左边界与右边界不重合for(int i = left;i < right;i++){//从左边界开始从左向右遍历if(ar[i] > ar[i + 1]){swap(ar,i,i + 1);}}right--;每从左至右遍历完一次右边界缩减一个单位for(int j = right;j > left;j--){//从右边界开始从右向左进行遍历if(ar[j - 1] > ar[j]){swap(ar,j - 1,j);}}left++;每从右向左遍历完一次左边界前移一个单位}
}
int main()
{srand((unsigned int)time(NULL));int ar[MAXSIZE];initar(ar,MAXSIZE);printf("原始数据为：\n");showar(ar,MAXSIZE);printf("\n经过鸡尾酒排序后的数据为：\n");Cocktail_sort(ar,MAXSIZE);showar(ar,MAXSIZE);return 0;
}程序验证：
我们在每次边界缩进的语句后方都添加一个打印函数语句用来验证我们上面的分析步骤，如图：
可以看到经过9趟排序之后函数最终完成了对数据的排序，和我们上面的分析一致。
对鸡尾酒排序的思考和优化：
我们对上面的排序过程进行分析，其实在Step 5时，序列就已经基本有序，Step6是对序列顺序的检查，后面的步骤也只是边界的缩进，也就是对循环条件while(left < right)的满足过程，其实Step7、8、9步骤是可以进行优化的，这一点和冒泡排序的优化十分类似因为鸡尾酒排序本身就是属冒泡类的排序方法。
在之前的文章：算法 - 冒泡排序（Bubble_ Sort）
https://blog.csdn.net/weixin_45571585/article/details/125174674?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166383825016800182755296%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=166383825016800182755296&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-125174674-null-null.nonecase&utm_term=%E5%86%92%E6%B3%A1&spm=1018.2226.3001.4450中曾经提到冒泡排序的优化：
void Bubble_sort(int *ar,int len)
{int flag = 1;while(len-- && flag){flag = 0;for(int i = 0;i < len;i++){if(ar[i] > ar[i + 1]){flag = 1;swap(ar,i,i + 1);}}}
}这里就是使用flag标签有效地去减少所要遍历的趟数，同样，我们也可以将次方法运用至鸡尾酒排序中：
#include<iostream>
using namespace std;
void Show(const int *a, int n)
{if(n<=0) return;cout << a[0];for(int i=1; i<n; i++)cout << ", " << a[i];cout << endl;
}void Show(const int *a, int n, int j)
{int i;if(n<=0) return;if(j==0)cout << "[" << a[0];elsecout << " " << a[0];for(i=1; i<n; i++){if(i==j)cout << ",[" << a[i];else if(i==j+1)cout << ", " << a[i] << "]";elsecout << ", " << a[i];}cout << endl;
}
void CocktailSort(int *a, int n)
{for(int i=0; i<n; i++){int flag = 1;if(i % 2 == 0){cout << "\n第" << i+1 << "轮(从左到右)" << endl;for(int j=i/2; j<1; j++)//后面对取i/2有说明{if(a[j] > a[j+1]){swap(a[j], a[j+1]);flag = 0;}Show(a, n, j);}}else{cout << "\n第" << i+1 << "轮(从右到左)" << endl;for(int j=n-1-i/2; j>i/2; j--){if(a[j-1] > a[j]){swap(a[j-1], a[j]);flag = 0;}Show(a, n, j-1);}}cout << "本轮" << (flag? "无" : "有") << "交换" << endl;if(flag)break;}
}
int main()
{int a[] = {8, 1, 0, 9, 7, 5};//嘿嘿嘿，整个活int n = sizeof(a)/sizeof(*a);cout << "原始数据: ";Show(a, n);CocktailSort(a, n);cout << "\n鸡尾酒排序结果: ";Show(a, n);return 0;
}
运行结果：
对鸡尾酒排序的总结：
鸡尾酒排序实际上是属冒泡排序类的，是冒泡排序的变体形式，它与冒泡排序之间的不同点就在就在于冒泡排序是单向的，而鸡尾酒是双向的。鸡尾酒排序的时间复杂度和冒泡排序一样，它们都是嵌套的双层循环，所以时间复杂度为O（n^2）,空间复杂度为O（1）。
鸡尾酒排序相较于冒泡排序可显著的减少排序所进行的趟数，但是相应的，代码量却增加了近一倍。
参考资料：
c++鸡尾酒排序（优化）_zedkyx的博客-CSDN博客鸡尾酒排序（优化）文章目录鸡尾酒排序（优化）前言一、鸡尾酒排序是什么？二、程序实现步骤1.引入库2.子函数1（输出函数）子函数2（鸡尾酒排序）主函数输出结果
![[英美文化][UMOOCs][英美概况]unit1-7答案分享](https://img-blog.csdnimg.cn/f33cd574d7ce4f9f9924e8cfd556055c.jpeg)
