《数据结构》（非408代码题）

链表

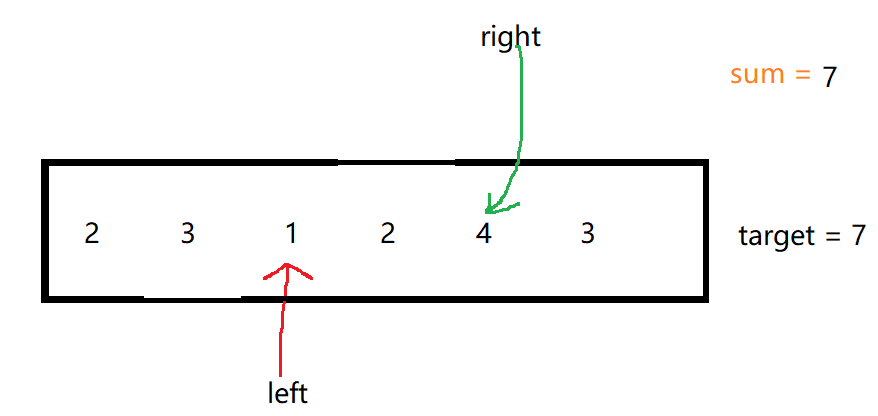
设单链表的表头指针为L，结点结构由data和next两个域构成，其中data域为字符型。试设计算法判断该链表的全部n个字符是否中心对称。例如xyx、xyyx都是中心对称。

分析：

这题完全可以参考19年那题，我们直接找到中间结点然后将后半段全部翻转，接着遍历一遍就好了（头指针和指向中间结点的那个指针同时向后直至后面那个指针指向空为止）唯一要额外考虑的是要是单链表长度为奇数时，要对正中间这个结点做点特殊处理，使其不参与后续的遍历比较。

struct Node {char data;Node* next;
};bool isSymmetric(Node* head) {if (!head || !head->next) return true; // 空链表或只有一个节点Node *slow = head, *fast = head;Node *prev = nullptr;// 找到中间节点，反转后半段链表while (fast && fast->next) {fast = fast->next->next; // 快指针每次走两步Node* nextNode = slow->next; // 保存下一个节点slow->next = prev; // 反转当前节点的指针prev = slow; // 移动前驱slow = nextNode; // 移动到下一个节点}// 如果链表长度为奇数，跳过中间节点if (fast) {slow = slow->next; // 跳过中间节点}// 比较前半段与反转后的后半段while (prev && slow) {if (prev->data != slow->data) {return false; // 不对称}prev = prev->next; // 移动前半段slow = slow->next; // 移动后半段}return true; // 对称
}

当然还有一种做法还是借助数组，第一轮遍历时，将其数值复制到数组当中。接着利用数组可以随机存取的特点，再从中间结点向两端比对即可。

struct Node {char data;Node* next;
};bool isSymmetric(Node* L) {std::vector<char> chars;Node* current = L;// 遍历链表并存储字符while (current != nullptr) {chars.push_back(current->data);current = current->next;}// 检查对称性int n = chars.size();for (int i = 0; i < n / 2; ++i) {if (chars[i] != chars[n - 1 - i]) {return false; // 不对称}}return true; // 对称
}

树

链式结构体

typedef struct BiTNode{int data;struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//BiTNode *p = BiTree p;
//BiTNode *p 偏向表示当前结点
//BiTree p 偏向表示当前结果为根的树typedef struct LNode{ElemType data;struct LNode* next;
}LNode,*LinkList;

二叉树的五种基本形态

空树
只有一个结点
有左子树，但右子树为空
有右子树，但左子树为空
左右两子树都不为空

递归遍历

递归算法理解：重点关注函数的功能（递和归）

二叉树的先序、中序和后序遍历

void PreOrder(BiTree T){if(T!=NULL){visit(T);                 //访问根结点PreOrder(T->lchild);      //递归遍历左子树PreOrder(T->rchild);      //递归遍历右子树}
}void PreOrder(BiTree T){if(T==NULL)    return;visit(T);                 //访问根结点PreOrder(T->lchild);      //递归遍历左子树PreOrder(T->rchild);      //递归遍历右子树}//另外两个也只是交换语句顺序而已

先序遍历中第n个结点的值

int n=0;
void findn(BiTree T,int cnt){if(T==NULL) return;n++;if(n==cnt){printf("%d",T->data);}findn(T->lchild,cnt);findn(T->rchild,cnt);
}

求data域等于key的结点

BiTree* g=NULL;    //全局变量
void findkey(BiTree T,int key){if(T==NULL) return;if(T->data==key)    g=T;    	//g只会赋值一次findkey(T->lchild,key);findkey(T->rchild,Key);
}

求二叉树所有的结点个数

//Way1：使用全局变量
int n=0;//全局变量，表示总结点数 
void cnt(BiTree T){if(T==NULL) return;n++;cnt(T->lchild);cnt(T->rchild);
}//Way 2：使用树的五种结构
int cnt(BiTree T){if(T==NULL) return 0;return 1+cnt(T->lchild)+cnt(T->rchild);
}

求二叉树所有叶子结点个数

//Way1：使用全局变量
int n=0;//全局变量，表示总结点数 
void cnt(BiTree T){if(T==NULL) return;if(T->lchild==NULL&&T->rchild==NULL){n++;		}cnt(T->lchild,k);cnt(T->rchild,K);
}//Way 2：使用树的五种结构
int cnt(BiTree T){if(T==NULL) return 0;else if(T->lchild==NULL&&T->rchild==NULL) return 1;//else if(T->lchild!=NULL&&T->rchild==NULL) return cnt(T->lchild);//else if(T->lchild==NULL&&T->rchild!=NULL) return cnt(T->rchild);return cnt(T->lchild)+cnt(T->rchild);
}

求二叉树所有的单分支结点

int cnt(BiTree T){if(T==NULL) return 0;else if(T->lchild==NULL&&T->rchild==NULL) return 0;else if(T->lchild!=NULL&&T->rchild==NULL) return 1+cnt(T->lchild);else if(T->lchild==NULL&&T->rchild!=NULL) return 1+cnt(T->rchild);return cnt(T->lchild)+cnt(T->rchild);
}

求二叉树所有的双分支结点

int cnt(BiTree T){if(T==NULL) return 0;else if(T->lchild==NULL&&T->rchild==NULL) return 0;else if(T->lchild!=NULL&&T->rchild==NULL) return cnt(T->lchild);else if(T->lchild==NULL&&T->rchild!=NULL) return cnt(T->rchild);return 1+cnt(T->lchild)+cnt(T->rchild);
}

求二叉树的高度

int high(BiTree T){if(T==NULL)    return 0;return max(high(T->rchild),high(T->lchild))+1;
}

判断两个二叉树是否相等

int same(BiTree a,BiTree b){if(a==NULL&&b==NULL)    return 1;else if(a!=NULL&&b==NULL)    return 0;else if(a==NULL&&b!=NULL)    return 0;else{if(a->data==b->data){return same(a->lchild,b->lchild)&&same(a->rchild,b->rchild);}else{return 0;}
}

判断两个二叉树是否相似

只要结构一样就好

int resemble(BiTree a,BiTree b){if(a==NULL&&b==NULL)    return 1;else if(a==NULL||b==NULL)    return 0;else{return resemble(a->lchild,b->lchild)&&resemble(a->rchild,b->rchild);}
}

二叉树的层次遍历

//层序遍历
void LevelOrder(BiTree T){LinkQueue Q;InitQueue(Q);                //初始化辅助队列BiTree p;EnQueue(Q,T);                 //将根节点入队while(!isEmpty(Q)){           //队列不空则循环DeQueue(Q,p);              //队头结点出队visit(p);                  //访问出队结点if(p->lchild != NULL)EnQueue(Q,p->lchild);   //若左孩子不空，左孩子入队if(p->rchild != NULL)EnQueue(Q,p->rchild);   //若右孩子不空，右孩子入队}
}

二叉树的层次遍历——变体（反转）

// 反转层序遍历
void ReverseLevelOrder(BiTree T) {LinkQueue Q;InitQueue(Q);                // 初始化辅助队列EnQueue(Q, T);               // 将根节点入队LinkStack S;InitStack(S);BiTNode *p, *s;while (!isEmpty(Q)) {         // 队列不空则循环DeQueue(Q, p);           // 队头结点出队Push(S, p);if (p->lchild != NULL)EnQueue(Q, p->lchild);   // 若左孩子不空，左孩子入队if (p->rchild != NULL)EnQueue(Q, p->rchild);   // 若右孩子不空，右孩子入队}while (!StackEmpty(S)) {Pop(S, s);printf("%d ", s->data);     // 打印节点数据free(s);                   // 释放节点内存}
}

交换二叉树的左右子树

void swap(BiTree T){if(T==NULL)    return;BiTNode* temp=T->lchild;T->lchild=T->rchild;T->rchild=temp;swap(T->lchild);swap(T->rchild);
}

层次遍历

//层序遍历
void LevelOrder(BiTree T){LinkQueue Q;InitQueue(Q);                //初始化辅助队列BiTree p;EnQueue(Q,T);                 //将根节点入队while(!isEmpty(Q)){           //队列不空则循环DeQueue(Q,p);              //队头结点出队visit(p);                  //访问出队结点if(p->lchild != NULL)EnQueue(Q,p->lchild);   //若左孩子不空，左孩子入队if(p->rchild != NULL)EnQueue(Q,p->rchild);   //若右孩子不空，右孩子入队}
}

求二叉树高度

int high(BiTree T) {if (T == NULL) return 0; // 空树高度为0LinkQueue Q;InitQueue(Q);EnQueue(Q, T); // 将根节点入队int size = 1; // 当前队列中的元素数量int high = 0; // 树的高度while (size != 0) {int level_size = size; // 当前层的节点数for (int i = 0; i < level_size; i++) {BiTNode *cur = DeQueue(Q); // 队头结点出队size--;if (cur->lchild != NULL) {EnQueue(Q, cur->lchild); // 若左孩子不空，左孩子入队size++;}if (cur->rchild != NULL) {EnQueue(Q, cur->rchild); // 若右孩子不空，右孩子入队size++;}}high++; // 每遍历完一层，高度加1}return high; // 返回二叉树的高度
}

求二叉树的宽度

int width(BiTree T) {if (T == NULL) return 0; // 空树宽度为0LinkQueue Q;InitQueue(Q);EnQueue(Q, T); // 将根节点入队int size = 1; // 当前队列中的元素数量int width = 0;while (size != 0) {int level_size = size; // 当前层的节点数width = max(level_size, width);for (int i = 0; i < level_size; i++) {BiTNode *cur = DeQueue(Q); // 队头结点出队size--;if (cur->lchild != NULL) {EnQueue(Q, cur->lchild); // 若左孩子不空，左孩子入队size++;}if (cur->rchild != NULL) {EnQueue(Q, cur->rchild); // 若右孩子不空，右孩子入队size++;}}}return width; 
}

求data域等于key的结点的层次号

int keyLevel(BiTree T, int key) {if (T == NULL) return -1; // 空树返回-1LinkQueue Q;InitQueue(Q);EnQueue(Q, T); // 将根节点入队int size = 1; // 当前队列中的元素数量int high = 0;int ans = -1; // 未找到key时的标记while (size != 0) {int level_size = size; // 当前层的节点数for (int i = 0; i < level_size; i++) {BiTNode *cur = DeQueue(Q); // 队头结点出队size--;if (cur->data == key) ans = high + 1;if (cur->lchild != NULL) {EnQueue(Q, cur->lchild); // 若左孩子不空，左孩子入队size++;}if (cur->rchild != NULL) {EnQueue(Q, cur->rchild); // 若右孩子不空，右孩子入队size++;}}high++;}return ans; // 返回找到的层数，未找到返回-1
}

判断二叉树是否为完全二叉树

int IsCompleteBinaryTree(BiTree T) {if (T == NULL) return 1; // 空树视为完全二叉树LinkQueue Q;InitQueue(Q);EnQueue(Q, T); // 将根节点入队while (!isEmpty(Q)) {BiTNode *cur = DeQueue(Q);if (cur != NULL) {EnQueue(&Q, cur->lchild);EnQueue(&Q, cur->rchild);} else {// 遇到空节点，检查下一个节点是否非空if (!isEmpty(Q)) {BiTNode *next = DeQueue(Q);if (next != NULL) {return 0; // 如果下一个节点非空，则不是完全二叉树}}}}return 1; // 遍历完所有节点，是完全二叉树
}

非递归排序

二叉树的先序、中序和后序遍历

先序/中序（输出语句的改变决定其是先还是中）：

循环结束条件：node为空且栈空
node不空，入栈，node到左孩子
node空，出栈，node到右孩子

后序：

循环结束条件：node为空且栈空
node不空，入栈，node到左孩子
node空取栈顶，看看右孩子，没有右孩子或者右孩子访问过，出栈标记，否则node到右孩子

注：因为每个结点都会被访问三次

// 先序遍历
void PreOrder(BiTree T) {LinkStack S;InitStack(S);BiTNode *node = T;while (node != NULL || !StackEmpty(S)) {if (node != NULL) {printf("%d ", node->data); // 访问节点Push(S, node);node = node->lchild;} else {node = Pop(S);node = node->rchild;}}
}// 中序遍历
void InOrder(BiTree T) {LinkStack S;InitStack(S);BiTNode *node = T;while (node != NULL || !StackEmpty(S)) {if (node != NULL) {Push(S, node);node = node->lchild;} else {node = Pop(S);printf("%d ", node->data); // 访问节点node = node->rchild;}}
}// 后序遍历
void PostOrder(BiTree T) {LinkStack S;InitStack(S);BiTNode *node = T;BiTNode *lastVisited = NULL;while (node != NULL || !StackEmpty(S)) {if (node != NULL) {Push(S, node);node = node->lchild;} else {BiTNode *topNode;GetTop(S, topNode); // 获取栈顶元素if (topNode->rchild == NULL || topNode->rchild == lastVisited) {printf("%d ", topNode->data); // 访问节点lastVisited = Pop(S); // 弹出节点} else {node = topNode->rchild;}}}
}

公共祖先

那这个不就是后续遍历非递归的变形题吗

void FindAncestors(BiTree T, int k) {BiTNode *p = T;BiTNode *r = NULL;LinkStack S;InitStack(S);while (p != NULL || !StackEmpty(S)) {if (p != NULL) {Push(S, p);p = p->lchild;} else {BiTNode *top;GetTop(S, top);if (top->rchild == NULL || top->rchild == r) {Pop(S);if (top->data == k) {while (!StackEmpty(S)) {BiTNode *ancestor = Pop(S);printf("%d ", ancestor->data->data);}return; // 找到k节点后打印所有祖先并返回}r = top;} else {p = top->rchild;}}}
}

孩子兄弟表示法

以二叉树的形式表示树或者森林

typedef struct CSNode{ElemType data;                               //数据域struct CSNode *firstchild, *nextsibling;     //第一个孩子和右兄弟指针
}CSNode. *CSTree;

求森林的叶子节点总个数

int leafNodeNum(CSTree root) {if (root == NULL) {return 0;} else if (root->firstchild == NULL) {// 如果没有子节点，返回1（当前节点作为叶子节点的一个路径）加上兄弟节点的路径数量return 1 + fun(root->nextsibling);} else {// 如果有子节点，返回左子树和右子树路径数量之和return fun(root->firstchild) + fun(root->nextsibling);}
}

求树的高度

int high(CSTree T) {if (T == NULL) {return 0; // 空树的高度为0} else {// 递归计算左子树的高度和右子树的高度，并返回最大值加1（当前节点）return max(fun(T->firstchild) + 1, fun(T->nextsibling));}
}

线索二叉树

//线索二叉树结点
typedef struct ThreadNode{ElemType data;struct ThreadNode *lchild, *rchild;int ltag, rtag;                // 左、右线索标志
}ThreadNode, *ThreadTree;

构建先序线索二叉树

ThreadNode *pre=NULL:void preThreadTree(ThreadTree p) {if (p == NULL) return;//====对这段代码移动===if (p->lchild == NULL) {p->lchild = pre;p->ltag = 1;}if (pre != NULL && pre->rchild == NULL) {pre->rchild = p;pre->rtag = 1;}pre = p;//====对这段代码移动===if (p->ltag == 0) {preThreadTree(p->lchild);}if (p->rtag == 0) {preThreadTree(p->rchild);}
}

线索二叉树的遍历（中序和先序）

// 获取线索二叉树的第一个节点
ThreadNode* firstNode(ThreadNode *p) {while (p->ltag == 0) p = p->lchild;return p;
}// 获取线索二叉树的下一个节点
ThreadNode* nextNode(ThreadNode *p) {if (p->rtag == 1)return p->rchild;elsereturn firstNode(p->rchild);
}// 遍历线索二叉树并访问每个节点
void visit(ThreadTree t) {for(ThreadNode *p = firstNode(t);p != NULL;p = nextNode(p)){printf("%d", p->data);}
}

ThreadNode* nextNode(ThreadNode *p) {if (p->tag == 0)return p->lchild;elsereturn p->rchild;
}
// 遍历线索二叉树并访问每个节点
void visit(ThreadTree t) {for(ThreadNode *p = t;p != NULL;p = nextNode(p)){printf("%d", p->data);}
}

二叉排序树

在二叉排序树中查找值为k的结点并返回

BiTNode* findk(BiTree t, int k){ if(t==NULL) return NULL; if(t->data==k) return t;else if(k>t->data) return findk(t->rchild, k); else return findk(t->lchild, k);
}

在二叉排序树中插入值为k的新结点，插入成功返回1，插入失败返回0

int insertk(BiTree &t, int k){if(t==NULL){t = (BiTNode*)malloc(sizeof(BiTNode)); t->data = k;t->lchild = NULL; t->rchild = NULL; return 1;}if(t->data==k) return 0;else if(k>t->data) return insertk(t->rchild, k); else return insertk(t->lchild, k);
}

注：在二叉排序树中不允许出现重复的值

判别二叉树是否为二叉排序树

int pre=-100000;
int ans=1;    //1表示二叉树排序树，0则不是
void BST(BiTree T){if(T==NULL) return; BST(T->lchild); if(pre>T->data){ ans=0;}pre=T->data; BST(T->rchild); 
}

指定结点在给定二叉排序树中的层次

void kNodeLevel(BiTree T,int level,int k){//传入根结点时 level=1 if(T==NULL) return;if(T->data==k) printf("%d" level); else if(k>T->data)kNodeLevel(T->rchild, level+1, k); elsekNodeLevel(T->Lchild, Level+1, k); 
}

图

邻接矩阵

邻接矩阵结构体

#define MaxVertexNum 100    //项目数目的最大值
typedef char VertexType;    //顶点对应的数据类型
typedef int EdgeType;    //边对应的数据类型
typedef struct{VertexType Vex[MaxVertexNum];    //顶点集EdgeType Edge[MaxVertexNum][MaxVertexNum];    //邻接矩阵，边表（也就是权重）int vexnum,arcnum;    //图的当前顶点数和边数
}MGraph;

注：行出度、列入度

采用邻接矩阵表示法创建无向网

// 创建无向图的邻接矩阵
void CreateMGraph(MGraph &G) {cout << "请输入顶点数和边数: ";cin >> G.vexnum >> G.arcnum;// 初始化顶点cout << "请输入顶点信息: ";for (int i = 0; i < G.vexnum; i++) {cin >> G.Vex[i];}// 初始化邻接矩阵for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {G.Edge[i][j] = (i == j) ? 0 : INT_MAX; // 自环为0，其他为无穷大}}// 输入边的信息cout << "请输入边的信息 (格式: 起点 终点 权重): " << endl;for (int k = 0; k < G.arcnum; k++) {char v1, v2;EdgeType weight;cin >> v1 >> v2 >> weight;int i = -1, j = -1;for (int m = 0; m < G.vexnum; m++) {if (G.Vex[m] == v1) i = m;if (G.Vex[m] == v2) j = m;}if (i != -1 && j != -1) {G.Edge[i][j] = weight; // 无向图G.Edge[j][i] = weight; // 无向图}}
}

邻接表

邻接表结构体

#define MaxVertexNum 100    //图中顶点数目的最大值
typedef struct ArcNode{    //边表结点int adjvex;    //该弧所指向的顶点的位置struct ArcNode *next;    //指向下一条弧的指针//InfoType info;    //网的边权值
}ArcNode;typedef struct VNode{    //顶点表结点VertexType data;    //顶点信息ArcNode *first;    //指向第一条依附该顶点的弧的指针
}VNode,AdjList[MaxVertexNum];typedef struct{AdjList vertices;    //邻接表int vexnum,arcnum;    //图的顶点数和弧数
}ALGraph;    //ALGraph是以邻接表存储的图类型

采用邻接表表示法创建无向网

// 创建无向图的邻接表
void CreateALGraph(ALGraph &G) {cout << "请输入顶点数和边数: ";cin >> G.vexnum >> G.arcnum;// 初始化顶点cout << "请输入顶点信息: ";for (int i = 0; i < G.vexnum; i++) {cin >> G.vertices[i].data;G.vertices[i].first = nullptr; // 初始化边表}// 输入边的信息cout << "请输入边的信息 (格式: 起点 终点): " << endl;for (int k = 0; k < G.arcnum; k++) {char v1, v2;cin >> v1 >> v2;int i = -1, j = -1;for (int m = 0; m < G.vexnum; m++) {if (G.vertices[m].data == v1) i = m;if (G.vertices[m].data == v2) j = m;}if (i != -1 && j != -1) {// 添加边 v1 -> v2ArcNode *newArc1 = new ArcNode{j, G.vertices[i].first};G.vertices[i].first = newArc1;// 添加边 v2 -> v1ArcNode *newArc2 = new ArcNode{i, G.vertices[j].first};G.vertices[j].first = newArc2;}}
}

邻接表的遍历（BFS、DFS）

// 深度优先搜索（DFS）
void DFS(ALGraph &G, int v, bool visited[]) {visited[v] = true; // 标记为已访问cout << G.vertices[v].data << " "; // 访问顶点ArcNode *arc = G.vertices[v].first;while (arc != nullptr) {if (!visited[arc->adjvex]) {DFS(G, arc->adjvex, visited); // 递归访问}arc = arc->next;}
}// 广度优先搜索（BFS）
void BFS(ALGraph &G, int v) {bool visited[MaxVertexNum] = {false}; // 访问标记queue<int> q;visited[v] = true; // 标记为已访问cout << G.vertices[v].data << " "; // 访问顶点q.push(v); // 入队while (!q.empty()) {int current = q.front();q.pop();ArcNode *arc = G.vertices[current].first;while (arc != nullptr) {if (!visited[arc->adjvex]) {visited[arc->adjvex] = true; // 标记为已访问cout << G.vertices[arc->adjvex].data << " "; // 访问顶点q.push(arc->adjvex); // 入队}arc = arc->next;}}
}

图的遍历

深度优先遍历

bool visited[MAX_VERTEX_NUM];
void DFSTraverse(MGraph G){int v; for(v=0; v<G.vexnum; ++v){visited[v] = FALSE;	//初始化已访问标记数据}for(v=0; v<G.vexnum; ++v){	//从v=0开始遍历if(!visited[v]){DFS(G, v);}}
}

广度优先遍历

//BFS伪代码
bool visited[Max_vertex_num];    //访问标记数组
void BFSTraverse(Graph G) {    for (int i = 0; i < G.vexnum; ++i)visited[i] = false;     //访问数组初始化InitQueue(Q);    //初始化辅助队列Qfor (int i = 0; i < G.vexnum; ++i){if(!visited[i])BFS(G, i);         //对每个连通分量调用一次BFS}
}