根据成绩预测大学生能否被高校录取

github源码和数据下载

1、首先，导入库，并且读取数据集。原来数据集是 .txt 结尾的。
由于原始数据中并没有给出每一列的列的名字，所以，我们自己加一个 “Exam 1”、"“Exam 2”、“Admitted”，我们最好列举前几行数据，确认一下是否读入了数据，并且，看一下数据的维度：

import numpy as np
import pandas as pd
import matplotlib.pyplot as pltimport os# 路径
path = 'LogiReg_data.txt'
# 原文件没有表头，加一个表头：'Exam1','Exam2','Admitted'
pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
# 输出读取数据
print(pdData)
pdData.head()
pdData.shape

结果：

2.将数据分成正负样本，利用散点图，大致看一下数据分布（不是必要步骤，而且因为数据只有两个维度，才添加了此步骤）

# 录取
positive = pdData[pdData['Admitted'] == 1]
# 未录取
negative = pdData[pdData['Admitted'] == 0]# fig表示窗口，ax表示坐标轴
fig, ax = plt.subplots(figsize=(10, 5))
# 散布点，c='b'表示蓝色。 marker='x'表示标记  label左为左上角的标签
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')# 绘图
plt.show()

绘图结果：

补充说明一下：Admitted 是标签，当标签为 1 时，认为是正样本；标签为 0 时，认为是负样本。而 pd Data[‘Admitted’] == 1，是一堆 True 和 false

3、逻辑回归
此部分，我们主要建立一个分类器：也就是求解 theta 值。然后设定阈值，根据阈值，判断是否被录取。
主要步骤如下：

（1）、定义 sigmoid 函数

# 定义sigmoid函数
def sigmoid(z):return 1 / (1 + np.exp(-z))

sigmoid 函数是将预测值（比如线性回归中的结果），映射为概率的一个函数。形式为：
在这里插入图片描述

# creates a vector containing 20 equally spaced values from -10 to 10
nums = np.arange(-10, 10, step=1)
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(nums, sigmoid(nums), 'r')
# 绘图
plt.show()

其中，自变量 z 为任意值，而 g(z) 的值域为（0,1），（0,1）也就是对应着概率的大小。曲线图如下
在这里插入图片描述

(2）定义模型，也就是预测函数

# 定义模型函数
# X 是样本数据，它的每一行都是一个样本，每一列为样本的某一个特征。
# theta 表示参数，它是我们通过学习获得的，其中，对于每一个特征，都对应一个 theta
def model(X, theta):return sigmoid(np.dot(X, theta.T))

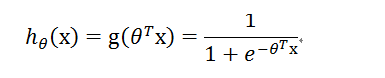
在这里插入图片描述
将 sigmoid () 函数的自变量 z 变成上式。其中，X 是样本数据，它的每一行都是一个样本，每一列为样本的某一个特征。theta 表示参数，它是我们通过学习获得的，其中，对于每一个特征，都对应一个 theta ,即
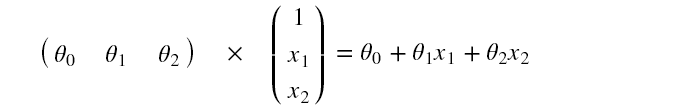
在这里插入图片描述
其中，为偏置项，因此，要在原始数据上补上一列，值为 1 ，是为了形式上的统一，方便矩阵运算，

# 在第 0 列，插入一列，名称为"Onces"，数值全为 1
pdData.insert(0, 'Onces', 1)
# X：训练数据   Y：目标值
# 将数据的panda表示形式转换为对进一步计算有用的数组
# 这个方法过时会有警告
orig_data = pdData.as_matrix()
cols = orig_data.shape[1]
X = orig_data[:, 0:cols - 1]
y = orig_data[:, cols - 1:cols]
# 初始化theta
theta = np.zeros([1, 3])X.shape, y.shape, theta.shape

(3) 定义损失函数

损失函数是将对数似然函数，乘以一个负号。乘以负号是为了将求解梯度上升转换为求解梯度下降
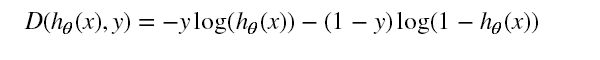
在这里插入图片描述
这是整体的一个损失，但是，不同的样本量，总损失肯定是不同的，因此，为了确定一个统一标准，使用平均损失，即将总损失除以样本个数，

# 定义损失函数
def cost(X, y, theta):left = np.multiply(-y, np.log(model(X, theta)))right = np.multiply((1 - y), np.log(1 - model(X, theta)))return np.sum(left - right) / (len(X))

使用print输出下面结果，结果是0.69314718055994529

# 将数值带入计算损失值
cost(X, y, theta)

（4）梯度的计算与参数的更新

计算梯度的目的是寻找极值，确定损失函数如何进行优化，使损失函数的值越来越小。
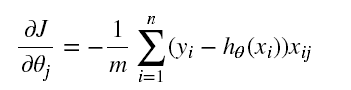
在这里插入图片描述
参数的更新策略为：

我们需要通过迭代来计算梯度，然后，梯度的计算什么时候停止呢？这里有三种停止策略：

1、设置固定的迭代次数

2、设置损失函数的阈值，当达到一定阈值时，就停止迭代。

3、通过梯度的变化率来判断：设置前后两次梯度相差的阈值，如果小于该阈值，停止迭代。

相关代码如下：

# 计算梯度
# 计算每个参数的梯度方向
def gradient(X, y, theta):grad = np.zeros(theta.shape)error = (model(X, theta) - y).ravel()for j in range(len(theta.ravel())):  # for each parmeterterm = np.multiply(error, X[:, j])grad[0, j] = np.sum(term) / len(X)return grad# 设置三种策略
STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2def stopCriterion(type, value, threshold):# 设定三种停止策略if type == STOP_ITER:return value > thresholdelif type == STOP_COST:return abs(value[-1] - value[-2]) < thresholdelif type == STOP_GRAD:# linalg=linear（线性）+algebra（代数），norm则表示范数return np.linalg.norm(value) < thresholdimport numpy.random# 洗牌
def shuffleData(data):np.random.shuffle(data)cols = data.shape[1]X = data[:, 0:cols - 1]y = data[:, cols - 1:]return X, yimport timedef descent(data, theta, batchSize, stopType, thresh, alpha):#  梯度下降init_time = time.time()# 迭代次数i = 0# batchk = 0X, y = shuffleData(data)# 计算的梯度grad = np.zeros(theta.shape)# 损失值costs = [cost(X, y, theta)]while True:grad = gradient(X[k:k + batchSize], y[k:k + batchSize], theta)# 取batch数量个数据k += batchSize# 这个 n 是在运行的时候指定的，为样本的个数if k >= n:k = 0# 重新洗牌X, y = shuffleData(data)# 参数更新theta = theta - alpha * grad# 计算新的损失costs.append(cost(X, y, theta))i += 1if stopType == STOP_ITER:value = ielif stopType == STOP_COST:value = costselif stopType == STOP_GRAD:value = gradif stopCriterion(stopType, value, thresh):breakreturn theta, i - 1, costs, grad, time.time() - init_timedef runExpe(data, theta, batchSize, stopType, thresh, alpha):# import pdb; pdb.set_trace();theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)name = "Original" if (data[:, 1] > 2).sum() > 1 else "Scaled"name += " data - learning rate: {} - ".format(alpha)if batchSize == n:strDescType = "Gradient"elif batchSize == 1:strDescType = "Stochastic"else:strDescType = "Mini-batch ({})".format(batchSize)name += strDescType + " descent - Stop: "if stopType == STOP_ITER:strStop = "{} iterations".format(thresh)elif stopType == STOP_COST:strStop = "costs change < {}".format(thresh)else:strStop = "gradient norm < {}".format(thresh)name += strStopprint("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(name, theta, iter, costs[-1], dur))fig, ax = plt.subplots(figsize=(12, 4))ax.plot(np.arange(len(costs)), costs, 'r')ax.set_xlabel('Iterations')ax.set_ylabel('Cost')ax.set_title(name.upper() + ' - Error vs. Iteration')return theta

这样，就可以运行结果了。运行的类型有很多种，首先，终止迭代的方式有三种，而选择样本的方式同样有三种：
（1）批量梯度下降，也就是一下子考虑所有的样本，这样的话，速度慢，但是容易得到最优解；
（2）随机梯度下降，每次只利用一个样本，这样的方式迭代速度很快，不过难以保证每次的迭代都是朝着收敛的方向；
（3）小批量梯度下降，即 mini-batch ，每次更新选择一小部分，比如 16个样本，32 个样本等等，这样的方式很实用，但应该先对数据进行洗牌，打乱顺序。

运行一下：

# 选择的梯度下降方法是基于所有样本的
# 当n值指定为10的时候,相当于整体对于梯度下降,为什么呢?因为我的数据样本就10个.
# 传进来的数据是按照迭代次数进行停止的,
# 指定迭代次数的参数是thresh=5000.学习率是alpha=0.000001.
n = 10
runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)
plt.show()

当n值指定为10的时候,相当于整体对于梯度下降,为什么呢?因为我的数据样本就10个.
传进来的数据是按照迭代次数进行停止的,指定迭代次数的参数是thresh=5000.学习率是alpha=0.000001.

运行结果：

如果采用随机梯度下降（每次只使用一个样本），或者小批量梯度下降（每次采用 mini-batch），会产生如下的效果——波动太大

# 设定阈值 1E-6, 差不多需要110 000次迭代
runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)
plt.show()

运行结果：

有至少两种解决方案：

（1）将学习率调小一点，情况肯定会有所改善

（2）对数据去均值化。将数据按其属性(按列进行)减去其均值，然后除以其方差。最后得到的结果是，对每个属性/每列来说所有数据都聚集在0附近，方差值为1。

from sklearn import preprocessing as ppscaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])

最终的结果是：波动不再明显，并且收敛速度加快，最终获得的损失函数的值会更小。不再一一列举实验

4、精度判断

预测

# 设定阈值
def predict(X, theta):return [1 if x >= 0.5 else 0 for x in model(X, theta)]scaled_X = scaled_data[:, :3]
y = scaled_data[:, 3]
predictions = predict(scaled_X, theta)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print('accuracy = {0}%'.format(accuracy))