-
归一化(Normalization)
- 定义
- 归一化是将数据映射到指定的范围,通常是[0, 1]或[- 1,1]区间。常见的归一化方法有:
- 线性函数归一化(Min - Max Scaling):公式为 x n e w = x − x m i n x m a x − x m i n x_{new}=\frac{x - x_{min}}{x_{max}-x_{min}} xnew=xmax−xminx−xmin,其中 x x x是原始数据, x m i n x_{min} xmin和 x m a x x_{max} xmax分别是数据集中的最小值和最大值。这种方法将原始数据线性地映射到[0, 1]区间。
- 非线性归一化(如对数归一化):例如 y = log ( x + 1 ) y = \log(x + 1) y=log(x+1)(当 x ⩾ 0 x\geqslant0 x⩾0时),这种方法适用于数据在一个方向上有较大的取值范围的情况。
- 归一化是将数据映射到指定的范围,通常是[0, 1]或[- 1,1]区间。常见的归一化方法有:
- 特点
- 归一化受数据的最大值和最小值影响较大。如果数据集中存在异常值,会对归一化的结果产生较大影响。
- 它保留了原始数据的分布形状,只是改变了数据的取值范围。
- 在一些对数据范围有要求的算法中应用广泛,比如在使用SVM(支持向量机)时,数据归一化可以使不同特征在相同的尺度上,有助于提高模型的收敛速度和性能。
- 定义
-
标准化(Standardization)
- 定义
- 标准化是将数据转换为均值为0,标准差为1的分布。其公式为 x n e w = x − μ σ x_{new}=\frac{x - \mu}{\sigma} xnew=σx−μ,其中 x x x是原始数据, μ \mu μ是数据集的均值, σ \sigma σ是数据集的标准差。
- 特点
- 标准化不受数据的量级和数据范围的影响,它基于数据的统计特性(均值和标准差)。因此,数据集中存在少量异常值对标准化的结果影响相对较小。
- 标准化后的数据符合标准正态分布(如果原始数据本身近似正态分布,标准化后更接近标准正态分布),这种特性使得它在很多基于正态分布假设的算法中非常有用,例如在使用基于正态分布假设的机器学习算法(如线性回归等)时,标准化数据有助于算法更好地收敛和工作。
- 定义
-
应用场景区别
- 归一化的应用场景
- 当需要将数据映射到特定区间时,如在图像处理中,将像素值归一化到[0, 1]区间,便于后续的计算和处理。
- 在一些对数据范围敏感的算法中,如神经网络中的某些激活函数(如Sigmoid函数),输入数据归一化到一个合适的范围可以使模型训练更加高效。
- 标准化的应用场景
- 在基于正态分布假设的统计分析和机器学习算法中广泛应用,如线性回归、逻辑回归、主成分分析(PCA)等。标准化可以使这些算法更好地处理数据,避免因为数据尺度不同而导致的模型偏差。
- 当数据集中存在少量异常值,但不希望这些异常值对数据转换产生过大影响时,标准化相对归一化是更好的选择。
- 归一化的应用场景
样本归一化还是标准化的
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/492350.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
【前端系列】Element-UI 悟道
???欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学习,不断总结,共同进步,活到老学到老…
中软高科身份证云解码金融(银行)解决方案介绍
多年来,中软高科一直深耕身份证云解码领域,对身份证云解码应用于金融(银行),进行了大量且深入的研究。从长期调研来看,金融(银行)的痛点需求主要有:
传统身份证解码设备…
【LeetCode】每日一题 2024_12_19 找到稳定山的下标(模拟)
前言
每天和你一起刷 LeetCode 每日一题~
最近力扣的每日一题出的比较烂,难度过山车,导致近期的更新都三天打鱼,两天断更了 . . .
LeetCode 启动! 题目:找到稳定山的下标 代码与解题思路
先读题:最重要…
SpringBoot开发——详解Tomcat线程池默认最大支持200并发
文章目录 1、SpringBoot 应用可以同时并发处理多少请求2、Tomcat线程池3、底层源码3.1 runWorker3.2 workQueue.offer 4、总结 1、SpringBoot 应用可以同时并发处理多少请求
Q:经典面试题,SpringBoot 应用可以同时并发处理多少请求? A&#…
Linux限制root 用户的远程登录(安全要求)
前言:现在基本用户主机都不允许使用root来操作,所以本文通过创建新用户,并限制root用户的ssh来解决这个问题
1. 创建新账户 aingo
首先,使用 root 账户登录系统。
sudo useradd aingo设置 aingo 账户密码:
sudo pa…
计算机网络之王道考研读书笔记-2
第 2 章 物理层
2.1 通信基础
2.1.1 基本概念
1.数据、信号与码元
通信的目的是传输信息。数据是指传送信息的实体。信号则是数据的电气或电磁表现,是数据在传输过程中的存在形式。码元是数字通信中数字信号的计量单位,这个时长内的信号称为 k 进制码…
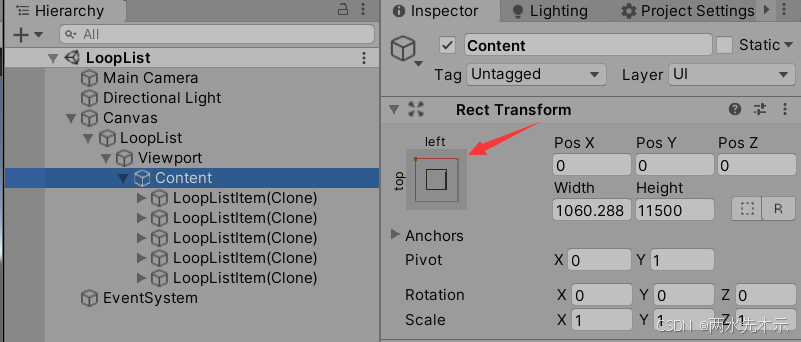
【Unity3D】无限循环列表(扩展版)
基础版:【Unity技术分享】UGUI之ScrollRect优化_ugui scrollrect 优化-CSDN博客 using UnityEngine;
using UnityEngine.UI;
using System.Collections.Generic;public delegate void OnBaseLoopListItemCallback(GameObject cell, int index);
public class BaseLo…
Hive SQL 查询所有函数
-- 显示所有的函数
show functions;
-- 对函数year进行解释
desc function year;
-- 对函数year进行详细解释,并举例说明
desc function extended year;– 对函数year进行解释 desc function year;
– 对函数year进行详细解释,并举例说明 desc functio…
Android13 系统签名应用编译调试说明
Android13 系统签名应用编译调试说明 文章目录 Android13 系统签名应用编译调试说明一、前言二、系统签名应用调试步骤1、新建一个应用,确保可以正常编译出APK2、获取系统签名文件3、Android Studio 编译安装系统权限应用(1)导入签名文件生成…
基于Spring Boot的医院质控上报系统
一、系统背景与意义
医院质控上报系统旨在通过信息化手段,实现医院质量控制的标准化、流程化和自动化管理。该系统能够帮助医院实时监控医疗质量数据,及时发现和处理潜在的质量问题,从而确保医疗服务的安全性和有效性。同时,系统…
将java项目部署到linux
命令解析 Dockerfile: Dockerfile 是一个文本文件,包含了所有必要的指令来组装(build)一个 Docker 镜像。 docker build: 根据 Dockerfile 或标准指令来构建一个新的镜像。 docker save: 将本地镜像保存为一个 tar 文件。 docker load: 从…
LeetCode:226.翻转二叉树
跟着carl学算法,本系列博客仅做个人记录,建议大家都去看carl本人的博客,写的真的很好的! 代码随想录 LeetCode:226.翻转二叉树 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 …
Webpack学习笔记(2)
1.什么是loader? 上图是Webpack打包简易流程,webpack本身只能理解js和json这样的文件,loader可以让webpack解析其他类型文件,并且将文件转换成模块供我们使用。 test识别出那些文件被转换,use定义转换时使用哪个loader转换
上图…
【WebDriver】浏览器驱动下载及其配置
一、Windows电脑环境搭建-Chrome浏览器
行业内,Chrome (谷歌) 浏览器对于自动化程序来讲是比较稳定的. 自动化程序推荐使用 Chrome 浏览器的原因有几个: 开发者工具:Chrome 提供强大的开发者工具,方便调试和测试自动化脚本。 稳…
【AIGC】如何高效使用ChatGPT挖掘AI最大潜能?26个Prompt提问秘诀帮你提升300%效率的!
还记得第一次使用ChatGPT时,那种既兴奋又困惑的心情吗?我是从一个对AI一知半解的普通用户,逐步成长为现在的“ChatGPT大神”。这一过程并非一蹴而就,而是通过不断的探索和实践,掌握了一系列高效使用的技巧。今天&#…
windows 使用python共享网络给另外一个网卡
# -*- coding: utf-8 -*-
import subprocessdef open_share(to_shared_adapter, from_shared_adapter):"""打开以太网的网络共享:return: None"""powershell_script f"""# Register the HNetCfg library (once)# regsvr32 hnetc…
devops-部署Harbor实现私有Docker镜像仓库
文章目录 概述下载配置安装安装后生成的文件使用和维护Harbor参考资料 概述
Harbor是一个开源注册中心,它使用策略和基于角色的访问控制来保护工件,确保镜像被扫描并且没有漏洞,并将镜像签名为可信的。Harbor是CNCF的一个毕业项目࿰…
Java深拷贝和浅拷贝区别?
大家好,我是锋哥。今天分享关于【Java深拷贝和浅拷贝区别?】面试题。希望对大家有帮助; Java深拷贝和浅拷贝区别?
1000道 互联网大厂Java工程师 精选面试题-Java资源分享网
在Java中,深拷贝(Deep Copy)和浅拷贝&am…
最新文章
推荐文章
- 【项目实战】犬只牵绳智能识别:源码详细解读与部署步骤
- (.htaccess文件特性)[MRCTF2020]你传你呢 1
- (11)(2.2) BLHeli32 and BLHeli_S ESCs(一)
- (2023Arxiv)Meta-Transformer: A Unified Framework for Multimodal Learning
- (3)(3.5) 遥测无线电区域条例
- (c++)类和对象 下篇
- (done 剩个什么 3/4 unigram frequency 的玩意儿没懂) word2vec 算法,计算 嵌入矩阵(CBOW, Skip-gram)随机梯度下降法 SGD 负采样方案
- (iFlyCode、FREEGPT、Copilot、AIPlus、稳定高效)分享好用的ChatGPT
- (JAVA)树——tree
- (UM1724) STM32 Nucleo-64 boards User manual
- (二)市场调查大赛系列——市场调查问卷设计
- (每日更新)《虚拟现实VR资讯》(Yanlz+Unity+SteamVR+云技术+5G+AI=VR云游戏=云渲染+人机交互+立钻哥哥+==)