文章目录

回顾：层次分析法的一些局限性

一、模型介绍

1.1 引例：

一个简单的想法：

一个较好的方法：

1.2 增加指标：

统一指标类型

标准化处理

计算得分

二、TOPSIS的介绍

第一步：将原始矩阵正向化

第二步：正向化矩阵标准化

第三步：计算得分并归一化

三、拓展：添加权重

*熵权法对TOPSIS模型的修正

度量信息量的大小

信息熵的定义

熵权法的计算步骤

熵权法背后的原理

四、代码实现

*熵权法加权

TOPSIS法（Technique for Order Preference by Similarity to Ideal Solution）可翻译为逼近理想解排序法，国内常简称为优劣解距离法。

TOPSIS 法是一种常用的综合评价方法，其能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。

回顾：层次分析法的一些局限性

1. 评价的决策层不能太多，太多的话n会很大，判断矩阵和一致矩阵差异可能会很大。

我们上面提到过的RI指标也只到了15：

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
R	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52	1.54	1.56	1.58	1.59

2. 如果决策层中指标的数据是已知的，那么我们如何利用这些数据来使得评价的更加准确呢？

该方法仍具有较强的主观性，判断/比较矩阵的构造在一定程度上是凭感觉决定的，一致性检验只是检验感觉有没有自相矛盾得太离谱。

如果题目中有已经提供了的数据，那就暗示我们不要用层次分析法了，我们可以通过分析这些数据内在的特征来进行建模。这就是TOPSIS方法应用于评价类问题与层次分析法不同之处。

一、模型介绍

1.1 引例：

坤坤宿舍共有四名同学，他们第一学期的高数成绩如下表所示：

姓名	成绩
坤坤	89
菜菜	60
小徐	74
鸡哥	99

请为这四名同学进行评估，该评分能合理的描述其高数水平的高低。

一个简单的想法：

姓名	成绩	等级level	排名	评分
坤坤	89	2	3	3/10=0.3
菜菜	60	4	1	1/10=0.1
小徐	74	3	2	2/10=0.2
鸡哥	99	1	4	4/10=0.4

可见，鸡哥成绩最高，最后评估得分0.4也是最高的。

但该方法存在一些问题：哪怕菜菜只得了0分，他的评价分数也是0.1，只与鸡哥差0.3分。

一个较好的方法：

我们构造评分公式：

$\frac{x-min}{max-min}$

其中，最高成绩max：99，最低成绩min：60。

则有：

姓名	成绩	归一化前的评分	归一化后的评分
坤坤	89	(89-60)/(99-60) = 0.74	0.74/2.1 = 0.35
菜菜	60	(60-60)/(99-60) = 0	0
小徐	74	(74-60)/(99-60) = 0.36	0.36/2.1 = 0.17
鸡哥	99	(99-60)/(99-60) = 1	1/2.1 = 0.48

这样的话，菜菜考得再低，鸡哥考得再高，评分还是不变的。

其实，按卷子满分是max:100，最低min：0。

姓名	成绩	归一化前的评分	归一化后的评分
坤坤	89	0.89	0.28
菜菜	60	0.60	0.19
小徐	74	0.74	0.23
鸡哥	99	0.99	0.30

这样显然更合理一些，菜菜最后的评分也不是0分了。

但是，我们依然选择max：99，最低成绩min：60，而不是max:100，最低min：0。原因如下：

比较的对象一般要远大于两个，例如比较一个班级的成绩。
比较的指标也往往不只是一个方面的，例如成绩、工时数、课外竞赛得分等。
- 菜菜的成绩是0，但也许他的其它项就把评分弥补回来了。
有很多指标不存在理论上的最大值和最小值，例如衡量经济增长水平的指标：GDP增速。

评分的公式：

$\frac{x-min}{max-min}$

1.2 增加指标：

新增加了一个指标，现在要综合评价四位同学，并为他们进行评分。

姓名	成绩	发生矛盾次数
坤坤	89	2
菜菜	60	0
小徐	74	1
鸡哥	99	3

成绩是越高（大）越好，这样的指标称为极大型指标（效益型指标）。
发生矛盾次数越少（越小）越好，这样的指标称为极小型指标（成本型指标）。

统一指标类型

为了方便评分，我们需要统一指标类型(就比如最开始成绩第一等级给他level4)；

将所有的指标转化为极大型称为指标正向化（最常用）：

姓名	成绩	发生矛盾次数	正向化后的争吵次数
坤坤	89	2	1
菜菜	60	0	3
小徐	74	1	2
鸡哥	99	3	0
指标类型	极大型	极小型	极大型

极小型指标转换为极大型指标的公式： max - x

标准化处理

姓名	成绩	正向化后的争吵次数
坤坤	89	1
菜菜	60	3
小徐	74	2
鸡哥	99	0

为了消去不同指标量纲的影响，需要对已经正向化的矩阵进行标准化处理。

如果我们直接计算，很明显成绩的数值大小远大于争吵次数，这就会导致结果过于倾向于成绩的高低，而争吵次数的影响微乎其微，因此，我们要对其进行 标准化处理。

标准化公式：

假设有n个要评价的对象，m个评价指标(已经过正向化处理)，构成矩阵X：

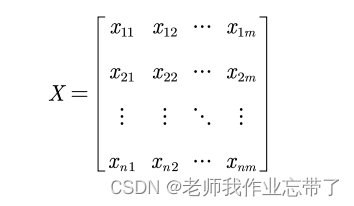
那么对其标准化的矩阵记为Z，Z中每个元素：

$z_{ij}=\frac{x_{ij}}{\sqrt{\sum_{i=1}^{n}}x_{ij}^{2}}$

如：

计算得分

姓名	成绩	正向化后的争吵次数
坤坤	0.5437	0.2673
菜菜	0.3665	0.8018
小徐	0.4520	0.5345
鸡哥	0.6048	0

当只有一个指标的时候，我们:

$\frac{x-min}{max-min}$

他可以看作：

$\frac{x-min}{(max-x)+(x-min)}$

即：

x与最小值的距离 / (x与最大值的距离+x与最小值的距离)

我们以 $D^{+}$ 表示与最大值的距离， $D^{-}$ 表示与最小值的距离，则：

对于坤坤：

$D^{+} = \sqrt{(0.6048-0.5437)^{2}+(0.8018-0.2673)^{2}} = 0.5380$
$D^{-} = \sqrt{(0.3665-0.5437)^{2}+(0-0.2673)^{2}} = 0.3206$

对于菜菜：

$D^{+} = \sqrt{(0.6048-0.3665)^{2}+(0.8018-0.8018)^{2}} = 0.2382$
$D^{-} = \sqrt{(0.3665-0.3665)^{2}+(0-0.8018)^{2}} = 0.8018$

对于小徐、鸡哥：略

得到下表：

姓名	$D^{+}$	$D^{-}$	归一化前的评分	归一化后的评分	排名
坤坤	0.5380	0.3206	0.3734	0.1857	3
菜菜	0.2382	0.8018	0.7709	0.3834	1
小徐	0.3078	0.5413	0.6375	0.3170	2
鸡哥	0.8018	0.2382	0.2291	0.1139	4

想不到，最后居然是成绩最低的菜菜综合测评排名第一！

当然，如果本学校更加看重成绩，也可以在第二步：标准化处理时设置权重。

二、TOPSIS的介绍

C.L.Hwang 和 K.Yoon 于1981年首次提出 TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution)，可翻译为逼近理想解排序法，国内常简称为优劣解距离法。

TOPSIS 法是一种常用的综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。

基本过程为先将原始数据矩阵统一指标类型（一般正向化处理）得到正向化的矩阵，再对正向化的矩阵进行标准化处理以消除各指标量纲的影响，并找到有限方案中的最优方案和最劣方案，然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制，数据计算简单易行。

第一步：将原始矩阵正向化

最常见的四种指标：

指标名称	指标特点	例子
极大型（效益型）指标	越大（多）越好	成绩、GDP增速、企业利润
极小型（成本型）指标	越小（少）越好	费用、坏品率、污染程度
中间型指标	越接近某个值越好	水质量评估时的PH值
区间型指标	落在某个区间最好	体温、水中植物性营养物量

所谓的将原始矩阵正向化，就是要将所有的指标类型统一转化为极大型指标。（转换的函数形式可以不唯一）

极小型指标 --> 极大型指标：

$max-x$ 或者 $\frac{1}{x}(\forall x>0)$

中间型指标 --> 极大型指标:

$\begin{Bmatrix} x_{i} \end{Bmatrix}$ 为一指标序列， $x_{best}$ 为最佳指标；

$M=max\begin{Bmatrix} |x_{i}-x_{best}| \end{Bmatrix}, \: \: \: \widetilde{x}_{i}=1-\frac{|x_{i}-x_{best}|}{M}$

如：

PH值(转换前)	PH值(转换后)
6	$1-\frac{\|6 - 7\|}{2}=\frac{1}{2}$
7	$1-\frac{\|7 - 7\|}{2}=1$
8	$1-\frac{\|8 - 7\|}{2}=\frac{1}{2}$
9	$1-\frac{\|9 - 7\|}{2}=0$

其中 $x_{best} = 7$ , $M=max\begin{Bmatrix} |6-7|,|7-7|,|8-7|,|9-7| \end{Bmatrix} = 2$

区间型指标 --> 极大型指标

$\begin{Bmatrix} x_{i} \end{Bmatrix}$ 为一指标序列， $[a,b]$ 为最佳区间；

$M=max\begin{Bmatrix} a-min(\begin{Bmatrix} x_{i} \end{Bmatrix}),max(\begin{Bmatrix} x_{i} \end{Bmatrix})-b \end{Bmatrix}$

$x_{i}=\left\{\begin{matrix} 1-\frac{a-x_{i}}{M} & x_{i}<a\\ 1 & a\leq x_{i}\leq b\\ 1-\frac{x_{i}-b}{M}& x_{i}>b \end{matrix}\right.$

如：

体温(转换前)	体温(转换后)
35.2	0.4286
35.8	0.8571
36.6	1
37.1	0.9286
37.8	0.4286
38.4	0

其中：a=36，b=37， $M = max\begin{Bmatrix} 36-35.2,\: 38.4-37 \end{Bmatrix}=1.4$

注意：正向化的公式不唯一，大家也可以结合自己的数据进行适当的修改。

第二步：正向化矩阵标准化

标准化的目的是消除不同指标量纲的影响。

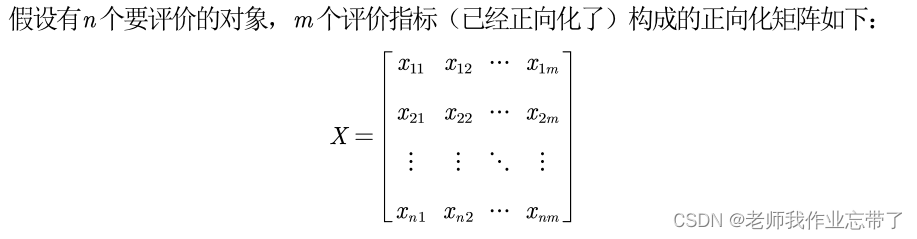
假设有n个要评价的对象，m个评价指标(已经过正向化处理)，构成矩阵X：

那么对其标准化的矩阵记为Z，Z中每个元素：

$z_{ij}=\frac{x_{ij}}{\sqrt{\sum_{i=1}^{n}}x_{ij}^{2}}$

注意：标准化的方法有很多种，其主要目的就是去除量纲的影响，未来我们还可能见到更多种的标准化方法，例如：(x‐x的均值)/x的标准差；具体选用哪一种标准化的方法在多数情况下并没有很大的限制，这里我们采用的是前人的论文中用的比较多的一种标准化方法。

第三步：计算得分并归一化

注意：

要区别开归一化和标准化。归一化的计算步骤也可以消去量纲的影响，但更多时候，我们进行归一化的目的是为了让我们的结果更容易解释，或者说让我们对结果有一个更加清晰直观的印象。例如将得分归一化后可限制在0‐1这个区间，对于区间内的每一个得分，我们很容易的得到其所处的比例位置。
这里还没有考虑指标的权重，后面的内容会考虑指标的权重来进行计算。

三、拓展：添加权重

在我们计算x与最大值的距离和 x与最小值的距离之前，也就是刚刚标准化完数据之后，可以指标进行权重的设置。

可以使用之前学的层次分析法来确定权重。

此时，我通过查阅资料，询问走访，自己一拍脑门对含氧量，PH值，细菌总个数，植物营养物量进行了打分(我自己乱打的分，略了)

权重结果	含氧量	PH值	细菌总个数	植物营养物量
含氧量	1
PH值		1
细菌总个数			1
植物营养物量				1

那么我们在代码中添加: # 加入权重的部分

上图也说了，我们也可以把权重加在标准化处理完成后的矩阵上，而不是距离公式上，结果几乎相同。

*熵权法对TOPSIS模型的修正

之前说过层次分析法判断矩阵的确定有很强的主观性。

熵权法是一种客观赋权方法

依据的原理：指标的变异程度越小，所反映的信息量也越少，其对应的权值也应该越低。

（客观 = 数据本身就可以告诉我们权重）

（一种极端的例子：对于所有的样本而言，这个指标都是相同的数值，那么我们可认为这个指标的权值为0，即这个指标对于我们的评价起不到任何帮助）

度量信息量的大小

小例子：

小红和小明是两个高中生，小明学习很差，小红学习很好，高考结束后二人都考上了清华。对于小红大家觉得这很正常，而小明考上了清华这就不一样了，这里面包含的信息量就非常大。

这个例子告诉我们：

越有可能发生的事情，信息量越少，越不可能发生的事情，信息量就越多。

那么我们怎么衡量事情发生的可能性大小？

概率

信息熵的定义

对于熵权法而言， 信息熵越大，信息量越小。因为我们关注的是已有的信息。

信息熵越大，说明它的值越大，能给你补充的信息量就越大，说明已有的信息量越小。

熵权法的计算步骤

1. 判断输入的矩阵中是否存在负数，如果有则要重新标准化到非负区间

我们前面所学，标准化得到Z

$z_{ij}=\frac{x_{ij}}{\sqrt{\sum_{i=1}^{n}}x_{ij}^{2}}$

本次我们需要去判断矩阵中是否存在负数(本身就是极大型)，如果存在，则需要对X使用另一种标准化方法：

$\widetilde{z}_{ij} = \frac{x_{ij}-min\begin{Bmatrix} x_{1j},x_{2j},...,x_{nj} \end{Bmatrix}}{max\begin{Bmatrix} x_{1j},x_{2j},...,x_{nj} \end{Bmatrix}-min\begin{Bmatrix} x_{1j},x_{2j},...,x_{nj} \end{Bmatrix}}$

2. 计算第j项指标下第i个样本所占的比重，并将其看作相对熵计算中用到的概率。

此时我们有了非负矩阵 Z，计算概率P：

$p_{ij}=\frac{\widetilde{z}_{ij}}{\sum_{i=1}^{n}\widetilde{z}_{ij}}$

注：这个还有上面和下面的公式都是固定列(指标)对所有行(对象)进行计算，即每一列所有的数据。

3. 计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权。

对于第j个指标而言，其信息熵的计算公式为：

$e_{j}=-\frac{1}{\ln n}\sum_{i=1}^{n}p_{ij}ln(p_{ij})$

定义: 0log0=0

熵权法背后的原理

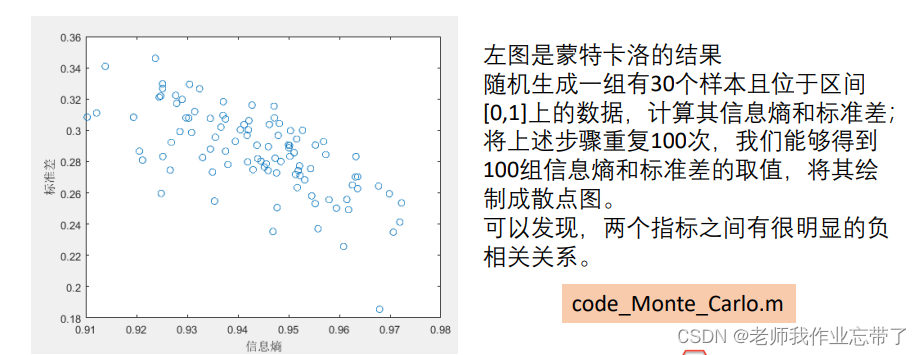
我们可以用指标的标准差来衡量样本的变异程度，指标的标准差越大，其信息熵越小。

四、代码实现

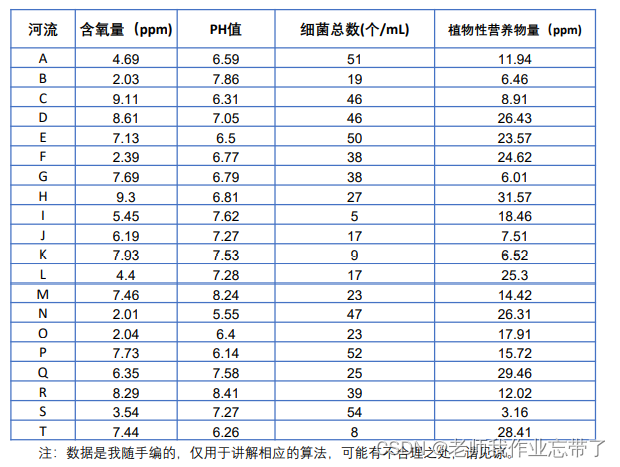
题目：评价下表中20条河流的水质情况。

注：含氧量越高越好；PH值越接近7越好；细菌总数越少越好；植物性营养物量介于10‐20之间最佳，超过20或低于10均不好

我们先将其指标正向化，再标准化再计算得分归一化，啪，就完成了。

ps: 下面代码可以设计得更智能一些，比如加入个input让你输入需要正向化的列是多少、正向化的方法是什么、是否加入权重、加入的权重又是多少，输入是否有误... 不过我觉得没必要。

import numpy as np
import pandas as pddata = pd.read_excel('20条河流的水质情况数据.xlsx')
matrix = data.loc[:, '含氧量（ppm)':].values# matrix第一列是极大型指标 我们对第二三四列进行正向化
# 注：正向化的公式不唯一，大家也可以结合自己的数据进行适当的修改。# 正向化类，这里返回拷贝后的result，也可以直接在原矩阵上进行修改。
class Index_calculation:def __init__(self, array):# 初始化指标序列self.array = array# 极小型 --> 极大型def samll_to_big(self):max_num = max(self.array)result = max_num - self.array# result = 1/self.arrayreturn result# 中间型 --> 极大型def middle_to_big(self, best):M = max(abs(self.array - best))result = 1 - abs(self.array - best) / Mreturn result# 区间型 --> 极大型def interval_to_big(self, a, b):M = max([a - min(self.array), max(self.array) - b])result = self.array.copy()result[result < a] = 1 - (a - result[result < a]) / Mresult[(a < result) & (result < b) | (result == a) | (result == b)] = 1result[result > b] = 1 - (result[result > b] - b) / Mreturn resultif __name__ == '__main__':# PH值越接近7越好col_2 = matrix[:, 1]# 细菌总数越少越好col_3 = matrix[:, 2]# 植物性营养物量介于10‐20之间最佳,超过20或低于10均不好。col_4 = matrix[:, 3]# 正向化matrix[:, 1] = Index_calculation(col_2).middle_to_big(7)matrix[:, 2] = Index_calculation(col_3).samll_to_big()matrix[:, 3] = Index_calculation(col_4).interval_to_big(10, 20)# 标准化for i in range(4):matrix[:, i] = matrix[:, i] / np.sqrt(sum(matrix[:, i] ** 2))# 求出 x与最大值的距离 和 x与最小值的距离D_big = np.sqrt(sum((max(matrix[:, i]) - matrix[:, i]) ** 2 for i in range(4)))D_small = np.sqrt(sum((min(matrix[:, i]) - matrix[:, i]) ** 2 for i in range(4)))# 得到未归一化前的得分s = D_small / (D_big + D_small)# 得分归一化fina_res = s / sum(s)

我们可以画图看一下这几条河流得分：

import matplotlib.pyplot as plt
%matplotlib inlineplt.rcParams['font.sans-serif']=['SimHei'] 
plt.rcParams['axes.unicode_minus']=False x = data['河流'].values
y = fina_resfig = plt.figure(figsize = (9,6))
plt.title('标题',fontsize = 15)
plt.xlabel('x轴',fontsize = 12)
plt.ylabel('y轴',fontsize = 12)
plt.ylim(0,max(y)*1.1)
plt.axhline(min(y),linestyle='--',color = 'grey')
plt.axhline(max(y),linestyle='--',color = 'orange')
plt.bar(x,y,color = 'lightblue',width = 0.6,linewidth = 0.5,edgecolor = 'r',tick_label = [a for a in x])# 最后一个参数加不下 都是下面显示abcd
plt.show()

可以看到河流K得分最高，N得分最低。

*熵权法加权

一些写法看个人喜好，还有一些正向化及标准化方法不唯一。

import numpy as np
import pandas as pddata = pd.read_excel('20条河流的水质情况数据.xlsx')
matrix = data.loc[:, '含氧量（ppm)':].values# 熵权法求权重weights
def get_weights(matrix):p = np.empty_like(matrix)for j in range(m):p[:, j] = matrix[:, j] / np.sum(matrix[:, j])e = np.empty(m)for j in range(m):array = p[:, j][p[:, j] != 0]  # 0*log0 = 0 我们直接把0去掉e[j] = -1 / np.log(n) * np.sum(array * np.log(array))d = 1 - eweights = d / np.sum(d)return weights# matrix第一列是极大型指标 我们对第二三四列进行正向化
# 注：正向化的公式不唯一，大家也可以结合自己的数据进行适当的修改。
# 正向化类，这里返回拷贝后的result，也可以直接在原矩阵上进行修改。
class Index_calculation:def __init__(self, array):# 初始化指标序列self.array = array# 极小型 --> 极大型def samll_to_big(self):max_num = max(self.array)result = max_num - self.array# result = 1/self.arrayreturn result# 中间型 --> 极大型def middle_to_big(self, best):M = max(abs(self.array - best))result = 1 - abs(self.array - best) / Mreturn result# 区间型 --> 极大型def interval_to_big(self, a, b):M = max([a - min(self.array), max(self.array) - b])result = self.array.copy()result[result < a] = 1 - (a - result[result < a]) / Mresult[(a < result) & (result < b) | (result == a) | (result == b)] = 1result[result > b] = 1 - (result[result > b] - b) / Mreturn resultif __name__ == '__main__':# PH值越接近7越好col_2 = matrix[:, 1]# 细菌总数越少越好col_3 = matrix[:, 2]# 植物性营养物量介于10‐20之间最佳,超过20或低于10均不好。col_4 = matrix[:, 3]# 正向化matrix[:, 1] = Index_calculation(col_2).middle_to_big(7)matrix[:, 2] = Index_calculation(col_3).samll_to_big()matrix[:, 3] = Index_calculation(col_4).interval_to_big(10, 20)n,m = matrix.shape# 标准化if np.min(matrix) < 0:for j in range(4):matrix[:, j] = (matrix[:, j] - np.min(matrix[:, j])) / (np.max(matrix[:, j]) - np.min(matrix[:, j]))else:for j in range(m):matrix[:, j] = matrix[:, j] / np.sqrt(sum(matrix[:, j] ** 2))# 调用函数 熵权法求解权重weights = get_weights(matrix)# 求出 x与最大值的距离 和 x与最小值的距离D_big = np.sqrt(sum(weights[j] * (max(matrix[:, j]) - matrix[:, j]) ** 2 for j in range(m)))D_small = np.sqrt(sum(weights[j] * (min(matrix[:, j]) - matrix[:, j]) ** 2 for j in range(m)))# 得到未归一化前的得分s = D_small / (D_big + D_small)# 得分归一化fina_res = s / sum(s)

之前我们没有加权值，如今这四个指标的权重为：

array([0.14106059, 0.22667469, 0.44093378, 0.19133094])

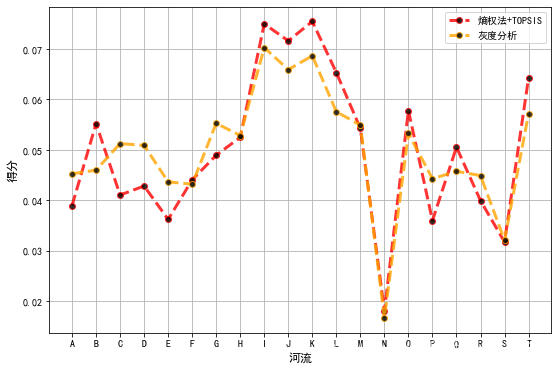
同样，我们再画图看一下添加权重后20条河流的得分：

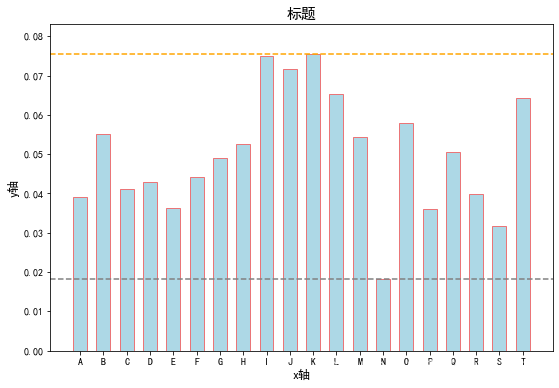
还是K最好，N最差。

ps:求权重的方法不同、权重加在数据上或者距离公式上、正向化及标准化方法不同，都可能导致最终结果有一点变换。

下期预告：灰度关联分析

PH值(转换前)	PH值(转换后)
6	$1-\frac{\|6 - 7\|}{2}=\frac{1}{2}$
7	$1-\frac{\|7 - 7\|}{2}=1$
8	$1-\frac{\|8 - 7\|}{2}=\frac{1}{2}$
9	$1-\frac{\|9 - 7\|}{2}=0$

【数学模型】TOPSIS

回顾：层次分析法的一些局限性

一、模型介绍

1.1 引例：

一个简单的想法：

一个较好的方法：

1.2 增加指标：

统一指标类型

标准化处理

计算得分

二、TOPSIS的介绍

第一步：将原始矩阵正向化

第二步：正向化矩阵标准化

第三步：计算得分并归一化

三、拓展：添加权重

*熵权法对TOPSIS模型的修正

度量信息量的大小

信息熵的定义

熵权法的计算步骤

熵权法背后的原理

四、代码实现

*熵权法加权

相关文章