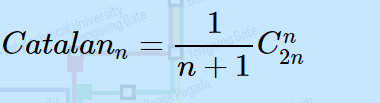复旦大学计算机机试

笔者最近打算刷一下各大高校的机试题，暂时不详细分类（可能是夏令营，预推免，也可能是考研机试。很有可能不全）

就按照学校分类一下：

先从最简单的复旦刷起。

题目来源是一个名叫N诺的网站，大家可以上去自己玩玩。

N诺

可自行注册一个账号

邀请码为：noobdream

题一 :求众数

分析：计数类首先想到Hash表，发现没有数字的取值范围，就老老实实用map。

因为c++的map有序，遍历一次就可以找到较小的那个众数。（不要用unordered_map）

#include <bits/stdc++.h>using namespace std;int main()
{int n;cin>>n;int a[n];map<int,int> m; //默认按照a[i]的大小排序for(int i=0;i<n;i++){cin>>a[i];m[a[i]]++;}int maxcnt=0,res=0;for(auto& it:m){if(it.second>maxcnt){res=it.first;maxcnt=it.second;}}cout<<res<<endl;return 0;
}

题二：解一元一次方程

#include <iostream>using namespace std;int main()
{string s;cin>>s;int sumx=0; //记录x前系数和int sumd=0;//记录常数和int num=0;int flag=1; //正负号int reve=1;//等号左右边int len=s.size();for(int i=0;i<len;i++){if(isdigit(s[i])){num=10*num+s[i]-'0';}if(s[i]=='x'){if(num==0) num=1;//x前没有缺省系数sumx+=num*flag*reve;num=0;}if(s[i]=='+'){sumd+=num*flag*reve;flag=1; //正号num=0; //为下一轮系数提取清零}if(s[i]=='-'){sumd+=num*flag*reve;flag=-1;num=0;}if(s[i]=='='){sumd+=num*flag*reve;flag=1;reve=-1;num=0;}}sumd+=num*flag*reve; //字符串末尾是没有结束符的，要再累计一次if(sumx==0&&sumd==0) cout<<"infinite solutions"<<endl;else if(sumx==0) cout<<"no solution"<<endl;else cout<<"x="<<(double)-sumd/sumx<<endl; //sumx * x+sumd=0 ,x=-sumd/sumxreturn 0;
}

题三：骨牌

#include <iostream>using namespace std;
/*
n=1 , 1
n=2 , 2
n=3 , 3
n=4 , 5
发现规律：f(n)=f(n-1)+f(n-2)  也可以从排放形状入手
带入知道，f(6)=13
*/int main()
{int n;cin>>n;if(n<=2){cout<<n<<endl;return 0;}int pre2=1;int pre1=2;int ans;for(int i=3;i<=n;i++){ans=(pre1+pre2)%999983;pre2=pre1;pre1=ans;}cout<<ans<<endl;return 0;
}

题四：集合交并

#include <bits/stdc++.h>using namespace std;int main()
{int n,m;cin>>n>>m;int a[n],b[m];set<int> s1;for(int i=0;i<n;i++){cin>>a[i];s1.insert(a[i]);}set<int> s2,s3(s1);for(int i=0;i<m;i++){cin>>b[i];if(s1.count(b[i])){ //s2用来存交集s2.insert(b[i]);}else{s3.insert(b[i]);//s3用来存并集}}cout<<s2.size()<<" "<<s3.size()<<endl;return 0;
}

题五：约数求和

#include <iostream>using namespace std;
/*
1 : 1
2 : 1 2
3 : 1 3
4 : 1 2 4
5 : 1 5
6 : 1 2 3 6
7 : 1 7
通过以上规律发现：1出现7/1次，2出现7/2次，3出现7/3次
i 出现 n/i次
*/int main()
{int n;cin>>n;long long ans=0;for(int i=1;i<=n;i++){ans+=(i)*(n/i);  }cout<<ans<<endl;return 0;
}

题六：求交点

#include <bits/stdc++.h>using namespace std;
/*
y=(x-x1)*(y2-y1)/(x2-x1)+y1
y=(x-x3)*(y4-y3)/(x4-x3)+y3解方程即可，但是注意，用乘积，少用除，防止出现除0. k1,k3不要算出来，展开了做
*/
int main()
{int x1,y1,x2,y2;int x3,y3,x4,y4;cin>>x1>>y1>>x2>>y2;cin>>x3>>y3>>x4>>y4;int a0=(y2-y1)*(x4-x3)-(y4-y3)*(x2-x1);if(a0==0){cout<<"Parallel or coincident"<<endl;}else{int a1=(x4-x3)*(y2-y1)*x1;int a2=(x2-x1)*(y4-y3)*x3;int a3=(x4-x3)*(x2-x1)*(y3-y1);double x=(double)(a1-a2+a3)/a0;double y=(x-x1)*(y2-y1)/(x2-x1)+y1;printf("%.2f %.2f",x,y);}return 0;
}

题七：长方形中的正方形

#include <iostream>using namespace std;/*
刚开始一看，有点儿像辗转相除的味道。
用递归写就好
递归函数recur(n,m)表示求的长方形长为n，宽为m的正方形个数
recur(n,m)=
1, n==m 
1+recur(n-m,m),n>m
1+recur(n,m-n),n<m递归三步走：
1.确定递归函数的意义
2.确定递归的方程
3.确定递归的初始条件*/
int recur(int n,int m){if(n==m) return 1;else{if(n<m) return 1+recur(n,m-n);else return 1+recur(m,n-m);}}int main()
{int n,m;cin>>n>>m;cout<<recur(n,m)<<endl;return 0;
}

题八：a与b得到c

#include <bits/stdc++.h>using namespace std;
/*
送分不解释，如果是经过有限次四则运算，就变成了dfs的题了
*/
int main()
{int a,b,c;cin>>a>>b>>c;set<double> s;s.insert(a+b);s.insert(a-b);s.insert(b-a);s.insert(a*b);s.insert((double)a/b);s.insert((double)b/a);if(s.count(c)) cout<<"YES"<<endl;else cout<<"NO"<<endl;return 0;
}

题九：相隔天数

#include <bits/stdc++.h>using namespace std;
/*
日期类问题，常规模拟，注意相隔多少天，要取绝对值。
这里没说错误提示，我就没有对日期进行错误判断了。
*/
bool isLeapYear(int year){return (year%4==0&&year%100!=0)||year%400==0;
}int month_day[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};int fromDays(int year,int month,int day){  //自1970：01：01int days=0;for(int i=1970;i<year;i++){if(isLeapYear(i)) days+=366;else days+=365;}for(int i=1;i<month;i++){days+=month_day[i];}if(isLeapYear(year)&&month>2) days++;days+=day;return days;
}int main()
{string s;cin>>s;int len=s.size();int year=0;int month=0;int day=0;for(int i=0;i<len;i++){if(i<4){year=10*year+s[i]-'0';}else if(i<6){month=10*month+s[i]-'0';}else{day=10*day+s[i]-'0';}}cout<<abs(fromDays(year,month,day)-fromDays(2019,2,5))<<endl;return 0;
}

题十：最大连续子序列

#include <bits/stdc++.h>
/*
非常简单的一个dp，
dp[i]表示以a[i]结尾的最大连续子序列
dp[i]=
dp[i-1]+a[i],dp[i-1]>0
a[i] ,dp[i-1]<=0最终答案res=max(res,dp[i])所有dp[i]的最大值
因为dp[i]只与dp[i-1]有关，于是可以压缩数组，为一个cur变量即可
*/
using namespace std;int main()
{int n;cin>>n;int a[n];int cur=0;int res=INT_MIN;for(int i=0;i<n;i++){cin>>a[i];cur=cur>0?cur+a[i]:a[i];res=max(cur,res);}cout<<res<<endl;return 0;
}

题十一：有向树形态

#include <iostream>using namespace std;/*
n=0, f(0)=1;
n=1 ,f(1)=1
n=2, f(2)=2
n=3, f(3)=f(2)+f(1)*f(1)+f(2)卡特兰数
f(n)=f(n-1)f(0)+f(n-2)f(1)+ ...+f(1)f(n-2)+f(0)f(n-1)f(n)=(2n)!/((n)!*(n+1)!)
*/long long f[21];int main()
{int n;cin>>n;f[0]=1;f[1]=1;for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){f[i]+=f[i-j]*f[j-1];}}cout<<f[n]<<endl;return 0;
}

2020夏令营机试（图片来源网上）

题一：拓扑排序模板

/*
测试用例：
4
1 0
2 0
3 1
3 2
-1 -1//结束标志
*/#include <bits/stdc++.h>using namespace std;vector<int> topo(int n,vector<vector<int>>& prerequist){vector<int> res;vector<int> indegrees(n);  //入度表vector<vector<int>> adj(n); //邻接表queue<int> zero;//度数为0的队列for(vector<int> tmp:prerequist){indegrees[tmp[0]]++;adj[tmp[1]].push_back(tmp[0]);}for(int i=0;i<n;i++){if(indegrees[i]==0) zero.push(i);}while(!zero.empty()){int tmp=zero.front();zero.pop();res.push_back(tmp);for(int j=0;j<adj[tmp].size();j++){if(--indegrees[adj[tmp][j]]==0) zero.push(adj[tmp][j]);}}return res.size()==n?res:vector<int>{};return res;
}int main()
{int n;cin>>n;  //输入没有进行太多处理，不是重点vector<vector<int>> prerequist;int x,y;while(cin>>x>>y) {vector<int> tmp;tmp.push_back(x);tmp.push_back(y);prerequist.push_back(tmp);if(x==-1){prerequist.pop_back();break;}}vector<int> res=topo(n,prerequist);for(int tmp:res){cout<<tmp<<" ";}cout<<endl;return 0;
}

题二：动规，等有时间再更新

备注：复旦这边题可以说，比较基础，大一的c语言学好都能做，有一些基础的数学找规律题。

可能是文理学校的缘故。