数学是编程的灵魂所在。

作者 | Justin Meiners
译者 | 王艳妮,责编 | 屠敏
出品 | CSDN(ID:CSDNnews)
以下为译文:
程序员喜欢讨论编程语言。除了辩论它们各自的优点外,我们还喜欢将它们整合到我们的身份认知中,甚至通过某人使用的语言来推断这是一个怎样的人。有些人甚至用语言决定论的一种形式争辩,认为思维受限于可被分类的东西的。
由于我们花了很多时间来使用语言,因此想要使它们变得更好的想法是合理的。然而,这些辩论的特点表明我们认为它们代表着更多的东西。也许我们忘记了语言本身最主要的作用。编程语言是实现工具,而不是思考工具。它们是严格的正式的语言,以人性化的方式来给机器下指令。相反,思想最好通过一种自由而灵活的媒介来表达。

用数学思考
数千年来,被高效地用于计算方面思考的自然语言就是数学。大多数人并不认为数学是自由的或灵活的。他们在学校看到可怕的符号和对解题步骤生硬记忆的经历与自由和灵活的数学精神恰恰相反。我希望本文的读者在数学方面有更好的经历,比如在离散数学或线性代数课程中; 那种涉及构建清晰的定义和演绎,并用符号写成散文(推理步骤)的经历(大多数符号甚至直到16世纪才被发明)。
数学允许你推理逻辑结构,而不受其他约束的影响。这也是编程所需要的:创建逻辑系统来解决问题。我们来看一下编程的基本模式:
找出问题所在
设计算法和数据结构来解决它
实现和测试
在实践中,工作往往组织得不是那么好,因为步骤之间存在相互作用。你可以编写代码来通知别人设计方面的问题。可即便如此,上面这个基本模式也一遍又一遍地在实践中重现。
请注意,步骤1和2是占用我们大部分时间,能力和精力的步骤。同时,这些步骤并不适合编程语言。这并不能阻止程序员尝试在他们的编辑器中解决它们,但他们最终会得到一些混乱,缓慢或解决了错的问题的代码。并不是编程语言还不够好。没有哪一种正式语言在这方面擅长。我们的大脑就不是那么思考问题的。当问题变得困难时,我们绘制图表并与同事们讨论。
理想情况下,首先解决步骤1和2,然后才使用编程语言来解决步骤3。这在转换实现过程中有额外的好处。有了数学解决方案,你就可以专注于选择最佳的表示和实现方式,编写更好的代码,了解最终目标将是什么。

实现问题
为什么编程语言作为思维工具是繁琐的?一个原因是编写代码与实现密不可分。实现问题对于给计算机下指令是必要的,并且值得做好,但它们也分散了在要解决的问题方面的注意力。想想如果要编写一个简单的函数,所有的注意事项:
我应该提供什么输入?
它们应该被命名为什么?
它们应该是什么类型的?(即使动态类型语言也必须考虑类型,它是隐含的而已。)
我应该通过值还是通过引用来传递它们?
我应该把这个函数放在什么文件中?
结果是否应该重复使用,或者它是否足够快以便每次重新计算?
这个列表还可以继续下去。关键是这些考虑因素与函数的作用无关。它们会分散人们对该函数试图解决的问题本身的注意力。
许多语言旨在隐藏诸如此类的细节,这对于普通的日常任务尤其有用。但是,它们无法超越其作为实现工具的角色。SQL很容易被认为是这方面最成功的例子之一,但它最终关注的还是表,行,下标和类型等实现方面的问题。正因为如此,程序员仍然在编写一堆JOIN之前,以随意的方式设计一些复杂的查询,比如一些他们想要“获取”的东西。

不灵活的抽象
编程语言的另一个限制是它们是糟糕的抽象工具。通常,当我们讨论工程中的抽象时,我们的意思是隐藏实现细节。一个复杂的操作或过程被打包成一个“黑盒”,其内容隐藏,并且暴露出明确定义的输入和输出。伴随着这个盒子的是一个关于它的功能的虚构故事,这很容易理解。
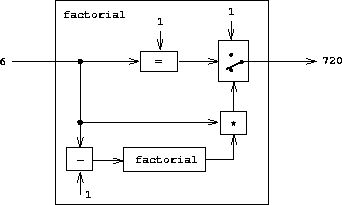
黑盒对于大型系统的工程设计至关重要,因为细节过多,对人脑来说理解起来压力山大。它们也有许多众所周知的局限性。黑盒泄漏是因为其简要的说明无法完全表述清楚其具体行为。不透明的界面引入了低效率,例如重复和分散设计。
最重要的是对解决问题来说,黑盒很僵硬。它们呈现出固定的抽象层级,这个层级可能对问题来说级别太高或太低。从理论上讲,你可以随时查看黑盒内部,但在代码中,任何时候的抽象级别都是固定的。它们也只提供了一种抽象视角。一个高级Web服务器可以提供用于服务JSON的极好的接口,但是如果你想要将其用于提供不完整数据流的接口(例如来自程序的输出)那它表现就很差了。
相比之下,数学中的抽象一词与隐藏信息完全不同。这里,抽象意味着提取与特定上下文相关的某些事物的基本特征或特征。与黑盒不同,这不会隐藏任何信息。它们不会以同样的方式泄漏。我们鼓励你调整到正确的抽象级别,并在不同角度之间快速跳转:
这个问题最好用表来表示吗?或者,一个函数?
我可以将整个系统视为一个函数吗?
我可以将这些东西作为一个整体处理吗?
我应该看整个系统还是单个部分?
我应该做出什么假设?我应该让它们更强还是更弱?
只需看看一个函数的多种表示方法:
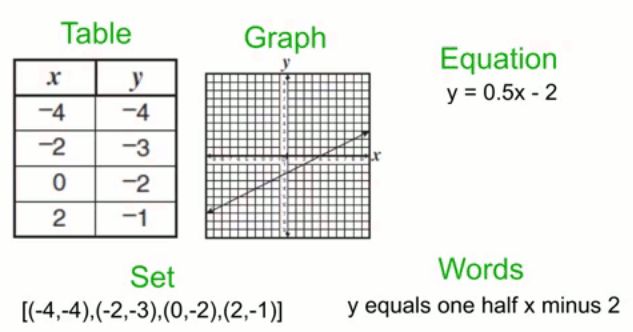
数学的主要分支代表了常用的抽象:
几何图形从世界中的物体中(或转换不变量,取决于想要获得的宇宙)抽象出基本形状。
拓扑从其形状中提取表面特征。
群论将二元运算抽象为关于它们如何组合和反转的属性。
但是,并不仅限于这几个领域。你可以选出对某个问题很重要的属性,并忽略其他。文章最后的示例项目显示了如何完成此操作。
编程语言非常适合构建黑盒; 它们提供了函数,类和模块,所有这些都有助于将代码包装到漂亮的接口中。但是,在尝试解决问题和设计解决方案时,你真正想要的是数学那样的抽象。如果你试着在键盘边上思考,可用的黑盒会扭曲你的视线。

问题表征
正如编程语言的抽象能力有限一样,它们在表示数据的方式上也受到限制。实现算法或数据结构的行为只是选择一个能表示它的许多可能的方式之一。通常,在你了解所需内容之前,这还不是一个你想现在就做出的决定。
例如,图(顶点和边的集合)出现在许多编程问题中,例如互联网网络,寻路和社交网络。尽管定义简单,但选择如何表示它们很难并且这取决于它们的使用情境:
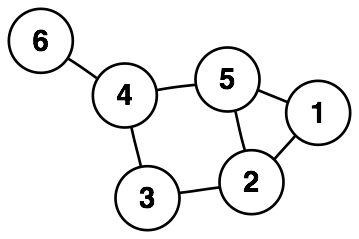
与定义最匹配的那个:
vertices:vector <NodeData> edges:vector <pair <Int,Int >>如果你只关心连接问题,可以删除顶点。
如果要快速遍历节点的邻接节点,那么你可能需要一个节点结构:
Node{id:Int,neighbors:vector <Node *>}
你可以使用邻接矩阵。每行存储特定节点的邻接节点:
connectivity:vector <vector <int >>
寻路算法通常在单元板上隐式地处理图:
walls:vector <vector <bool >>
在对等网络中,每台计算机都是一个顶点,每个插槽都是一个边。整个图表甚至无法从一台机器访问!
数学允许你对图本身进行推理,解决问题,然后选择合适的表达方式。如果你使用编程语言进行思考,则不能延迟此决定,因为你的第一行代码就是为了特定的表达而存在的。
请注意,图的表示太多样化,无法限于单一种类的接口,类型类(tpyeclass)甚至程序。因此,创建一个可完全复用的库是不切实际的。它只能在几种类型上工作,或者强制所有图使用不恰当的表示。但这并不意味着库没用。类似的表示会重复出现(比如std :: vector),但你没法写一个能一劳永逸地解决所有图形问题的库。
一些现代编程语言试图提供更多的数学抽象工具。例如,Haskell有Ring和Group类型类(typeclass)。然而,表示问题表明这些特征肯定不如它们的理论灵感有用。编写一个仅依赖于关联属性并且就那样存档的算法是明智的。这就是用数学语言思考。但是,实际上,这只能适度地处理相似类型的小家族。考虑几种类型的简单通用是合适的。
作为必然结果,编程语言应该主要将注意力放在如何做好一个有用的实现工具,而不是思考工具上。C在很大程度上做到了这一点。C#的异步和等待等现代语言功能为实现并发程序提供了很大的改进。

示例项目
那么用数学思考是什么样的一个过程呢?最近,我在工作中研究了一个API,它为商家的加密货币定价。它考虑了最近的价格变动,并建议商家在动荡时期收取更高的价格。
虽然我们在理论上做了一些功课,但我们想通过实证检验它以了解它在各种市场条件下的表现。为此,我设计了一个机器人来模拟与我们的API开展业务的商家,以了解它的表现。
BTC / USD(1天)
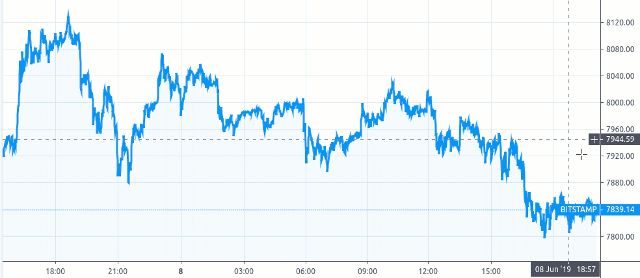
预备步骤:
定义:汇率r(t)是法定/加密货币的市场汇率。
定义:商家费率r'(t)是商家被建议向客户收费的修改后的汇率。
定义:当客户购买商品时,我们称该行为是“购买”。购买包括法定价格和时间。p =(f,t)。
定理:通过应用修改的汇率t(p)= p(1)/ r'(p(2))找到购买的加密量。
证明:p(1)/ r'(p(2))= fiat /(fiat / crypto)= fiat * crypto / fiat = crypto
定义:当商家出售他们的加密资产时,我们将该事件称为销售。销售包括加密金额和时间戳。s =(c,t)。
定理:通过将汇率应用于销售g(s)= s(1)* r(s(2))来找到商家从销售中获得的法定金额。
证明:s(1)* r(s(2))= 加密*(法定/ 加密)=法定
定义:一组购买和销售的余额是所有购买加密金额和所有销售加密金额之间的差额。b(P,S)=从t到p(p_i)的i到N之和 - 从j到M的s_j(1)之和
请注意,b(P,S)> = 0必须始终成立。
定义:一组购买和销售的收益是销售法定金额和购买法定金额之间的差额。e(P,S)=(s_j(1))从j到M的总和- p_i(1)从i到N的和> = 0。
目的
定义:如果大多数典型的购买和销售收入都是非负的,我们说商家利率是有利的。
r'(t) is favorable iff e(P, S) >= 0.
在一个有利的案例中,商人通过接受加密并没有失去任何法定货币。
“大多数”和“典型”的两个要求将不会被严格定义。
作为典型的一部分,我们可以假设商家会及时出售他们的加密资产。因此,假设s_i(2) - s_j(2)<W在i,j属于{1 .. M}范围内时成立,某些约束W.购买金额应随机分布在商业行为完成的合理范围内。也许10-100美元。
机器人的目标是验证r'(t)是有利的。
请注意,此定义只是质量的一种衡量标准。也许抵制最坏的情况比有利更重要。在这种情况下,我们会担心可能会进行一组收益非常低的购买。
算法
重复多次:
随机选择时间范围[t0,t1]。
在[t0,t1]内的随机时间生成一组购买。价格应该在典型价格的[p0,p1]范围内。
在[t0,t1]内以均匀间隔时间(可能具有轻微随机噪声)生成一组销售额。每次销售应该是当时的全部余额。
计算这些集合的收入。
记录收入。
后:
报告有多少收入为负数,有多少为非负数。显示每个的百分比。
确定最低和最高收入并报告。

总结
当你阅读这个例子时,我认为你的倾向可能是认为它的陈述是显而易见的。当然,这些步骤都不是很难。然而,令我惊讶的是,我的许多假设得到了纠正,选择有利结果的客观定义是多么困难。这个过程让我意识到一些如果我从简单编写代码开始的话,就压根不会考虑的假设。也许最大的好处是,在编写之后,我能够与同事一起快速审查它并进行简单的更正,但在代码中很难改变。
我希望用数学语言思考会给你的项目带来类似的好处!请注意,此示例只是一种利用数学思维的方式。我建议读Leslie Lamport,Udi Manber和Alex Stepanov等等其他人的想法。
原文:https://justinmeiners.github.io/think-in-math/
本文为 CSDN 翻译,转载请注明来源出处。



热 文 推 荐
☞开发小程序遇协同、平台兼容难题,该如何破局?
☞ 微软再称王
GitHub断供危机来了!权威解读程序员应对指南
☞ 真看不懂程序员的骚操作! | 每日趣闻
☞5G+AI重新定义生老病死
☞干货 | 20个Python教程,掌握时间序列的特征分析(附代码)
☞ 阿里云十年,从去“IOE”到引领云原生浪潮
☞ 知名饮料制造商股价暴涨500%惊动FBI,只因在名字中加入了"区块链" ?
为什么雷军说“华为不懂研发”?