熵大概是统计学、信息学中最让人纠结的基本概念之一。很多的人对于熵是什么多多少少能说出一二,但是不能准确的表达出来。我们都知道熵可以用来描述含有的信息丰富程度的多少,但具体指什么呢?
在讲到熵之前,在这里我先讲一个“自信息”
目录
1.自信息(信息量)
2.熵的引入
3.信息熵(香农熵)
3.1基本性质或特点
1)基本性质1: 若事件x的所有状态n发生概率都一致,即都为1/n,那么信息熵H(x)有极大值
2)基本性质2: 对于两个相互独立的事件,它们的信息熵是可加的
3)基本性质3: 加入发生概率为0的结果并不会有影响
4)基本性质4: 不确定性的度量应该是连续的
5)唯一性定理
6)特点: 具有更多可能结果的均匀分布有更大的不确定性
4.其他熵
4.1.联合熵(Joint Entropy)
4.2.条件熵(Conditional Entropy)
信息增益比
4.3.交叉熵(cross entropy)
4.4.相对熵(Relative Entropy)
4.5.互信息(Mutual Information)
1.自信息(信息量)
事件A:巴西队进入了2018世界杯决赛圈。
事件B:中国队进入了2018世界杯决赛圈。
仅凭直觉来说,显而易见事件B的信息量比事件A的信息量要大。究其原因,是因为事件A发生的概率很大,事件B发生的概率很小。所以当越不可能的事件发生了,我们获取到的信息量就越大。越可能发生的事件发生了,我们获取到的信息量就越小。
在生活中,极少发生的事情最容易引起吃瓜群众的关注。而经常发生的事情则不会引起注意,比如吃瓜群众从来不会去关心明天太阳会不会东边升起。
也就是说,信息量的多少与事件发生概率的大小成反比。
对于已发生的事件i,其所提供的信息量为:
![]()
其中对数的底数通常为2,也可以为10或e (在这里多谈一句,关于对数的计算,物理上常用e,数学计算中常用10,计算机相关常用2 。对数底数为e、2或者10之间存在 常数倍 关系,所以底数为什么都不影响最终结果,详解看 对数底数为e、2、10之间的关系转化),负号的目的是保证信息量不为负值。单位为bit
事件发生的概率与其对应的信息量的关系如下图所示:

2.熵的引入
熵这个概念对物理学、化学都很重要,它表示一个系系统在不受外部干扰时,其内部最稳定的状态。
我们知道,任何粒子的常态都是随机运动,也就是"无序运动",如果让粒子呈现"有序化",必须耗费能量。所以,温度(热能)可以被看作"有序化"的一种度量,而"熵"可以看作是"无序化"的度量。
1948年,香农Claude E. Shannon引入信息(熵),将其定义为离散随机事件的出现概率。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。所以说,信息熵可以被认为是系统有序化程度的一个度量。
即 熵通常被描述为一种对混乱度的度量单位。
举个很简单栗子:
假设你在医生办公室中与三个等待的病人交流。三个病人都刚刚完成药物测试,他们面临着两种可能的结果:患病或者未患病。假设这三个病人都充满好奇心而且数学好。他们提前各自研究得到了自己患病的风险,并且想通过这些来确认自己的诊断结果。
病人 A 知道他自己有 95% 的可能会患病。对于病人 B,患病概率为 30%,病人 C 的患病未患病的概率都为 50%。
显而易见,病人C具有最大的不确定性,而病人A的不确定性最弱,而病人B的不确定性介于病人A与病人C之间。
而熵这个概念的引入,就是用来描述这种不确定性的强弱的。
3.信息熵(香农熵)
在机器学习领域中,我们提到的熵都是信息熵。 在下面如果没有特别的指出,那么熵就是指的信息熵
H(x)表示用以消除这个事件的不确定性所需要的统计信息量,即信息熵。
在没有特意说明的情况下,下面就是熵的公式。对于事件X,有n种可能结果,且概率分别为p_1, ... p_n,公式为:
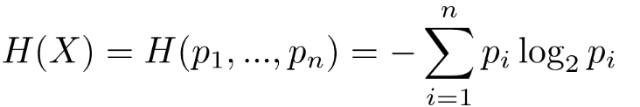
接下来我们来看看熵的基本性质或特点有哪些。
3.1基本性质或特点
1)基本性质1: 若事件x的所有状态n发生概率都一致,即都为1/n,那么信息熵H(x)有极大值
简单回顾一下概率分布:概率分布是一个函数,对于每个可能的结果都有一个概率,且所有的概率相加等于 1。
熵满足一个条件,就是均匀分布具有最大的熵,比如:抛硬币的正反面两面概率都是1/2,摇色子的每个点出现的概率都是1/6,此时信息熵具有极大值。
对于伯努利试验中熵的图像如下(伯努利试验中,有两种可能的结果:p和1-p):

所以在伯努利试验中,当p=0.5的时候,信息熵最大;当p=0或1的时候,信息熵最小。
2)基本性质2: 对于两个相互独立的事件,它们的信息熵是可加的
事件X=A,Y=B,如果同时发生,且相互独立,则可以得出:P(X=A,Y=B)=P(X=A)·P(Y=B)
那么信息熵为: H(X,Y)=H(X)+H(Y)
补充一下,对于两个不相互独立的事件,信息熵为: H(X,Y)=H(X)+H(Y)- I(X,Y),其中I(X,Y) 为互信息
3)基本性质3: 加入发生概率为0的结果并不会有影响
例如抛硬币试验,正面朝上的概率是1/2,反面朝上的概率是1/2,竖着的概率为0 。
根据信息熵H(X)公式就可以得知,加入发生概率为0的结果,并不会影响对不确定性的度量
4)基本性质4: 不确定性的度量应该是连续的
连续性的最直观的解释就是没有断开或者空洞。更精确的解释是:输出(在我们的场景下是不确定性)中任意小的变化,都可以由输入(概率)中足够小的变化得到。
对数函数在定义域上每个点都是连续的。在子集上有限数量函数的和和乘积也是连续的。由此可能得出熵函数也是连续的。
5)唯一性定理
Khinchin(1957)证明,满足上述四种基本性质的唯一函数族具有如下形式:

其中λ是正常数。Khinchin称之为唯一性定理。将λ设为1,并使用以2为底的对数就得到了香农熵。
6)特点: 具有更多可能结果的均匀分布有更大的不确定性
比如你可以在抛硬币试验和抛骰子试验中做出一个选择,如果硬币正面朝上(概率为1/2)或者骰子1朝上(概率为1/6)就算赢。你会选择哪个试验?如果你想最大化收入,肯定会选择硬币。如果只是想体验下不确定性,那可能就会选骰子。
随着等概率结果的数量的增加,不确定性的度量也应该增加。
这正是熵所做的:H(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)> H(0.5, 0.5)
所以均匀分布具有最大的熵是相对于同一个事件的而言的,如果是不同的事件,结果的数量越多,它的信息熵也就越大。
这就意味着,在决策树算法的计算中,用熵来计算是有短板的。
举个栗子:
你要判断一个人是否能生孩子,给出了两个特征列:性别(男,女),政治面貌(群众,共青团员,预备党员,中共党员)。
很明显,我们要判断一个人是否能生孩子,只需要知道他是 男 还是 女 就可以了,不需要知道政治面貌。但是因为 政治面貌 有4个结果数,而 性别 只有2个结果数,则 政治面貌 的 熵 会更大,所以在决策树中他会选择 政治面貌 来判断一个人是否能生孩子,这显然是不合理的。
那么在这里就需要引入一个概念——信息增益比 (具体计算方式看下方 条件熵 内) 来解决这个问题
4.其他熵
4.1.联合熵(Joint Entropy)
我们上面考虑的主要是单个事件发生的情况,假如两个事件同时发生,那么应该怎么考虑呢?
例如我们同时 抛两枚硬币 那么会出现四种结果:正正,正反,反正,反反,要怎么去度量计算它的信息熵呢?
这个时候就需要使用联合熵。两个离散随机变量X和Y的联合概率分布函数为p(X,Y),则联合熵公式如下:

其中p(x,y)代表事件x和事件y的联合概率。
举个小栗子:
这次以同时抛两枚硬币为例来说明联合熵如何对两个事件进行度量(对数的底数为2):
| 事件 | 联合概率 | 自信息量 | 联合熵 |
| x正,y正 | 1/2 * 1/2 = 1/4 | -log(1/4) | -(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4) |
| x正,y反 | 1/2 * 1/2 = 1/4 | -log(1/4) | -(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4) |
| X反,y正 | 1/2 * 1/2 = 1/4 | -log(1/4) | -(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4) |
| X反,y反 | 1/2 * 1/2 = 1/4 | -log(1/4) | -(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4) |
H(X,Y)=-(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4)-(1/4*log(1/4)=2 (四个事件,每个事件出现的联合概率代入进去计算)
4.2.条件熵(Conditional Entropy)
信息熵是代表随机变量的复杂度(不确定度),条件熵代表在某一个条件下,随机变量的复杂度(不确定度)。
条件熵表示在已知事件x的条件下,事件y的不确定性,即x发生的前提下,y发生的熵。定义为在给定条件下x,y的条件分布概率的熵对x的数学期望:
 条件熵与联合熵的公式仅仅log对数项上不同。
条件熵与联合熵的公式仅仅log对数项上不同。
条件熵与联合熵的关系:H(X|Y)=H(X,Y)-H(X)。即在x条件下,y的条件熵 = x,y的联合熵 - x的信息熵

信息增益比
信息增益 = 信息熵 - 条件熵
信息增益比 = (信息熵 - 条件熵 )/结果数 (比如骰子有6个面,那么摇骰子的结果数就为6)
信息增益代表了在一个条件下,信息复杂度(不确定性)减少的程度
4.3.交叉熵(cross entropy)
交叉熵是一个用来比较两个概率分布p和q的度量公式。换句话说,交叉熵是衡量在真实分布下,使用非真实分布所制定的策略能够消除系统不确定性的大小。
如何正确理解上述这段描述呢?首先,观察交叉熵的公式,如下图所示:

其中,p(x)为事件的真实分布概率,q(x)为事件的非真实分布概率。
可以看到,与信息熵相比,唯一不同的是log里的概率由信息熵中的真实分布概率p(x)变成了非真实概率(假设分布概率)q(x),即1-p(x)。也就是与信息熵相比,交叉熵计算的不是log(p)在p下的期望,而是log(q)在p下的期望。
同样地,交叉熵可也以推广到连续域。对于连续随机变量x和概率密度函数p(x)和假设分布概率密度函数q(x), 交叉熵的定义如下:

所以,如果假设分布概率与真实分布概率一致,那么交叉熵 = 信息熵。
4.4.相对熵(Relative Entropy)
相对熵又称KL散度,KL距离。
相对熵衡量了当修改从先验分布p到后验分布q的信念后所带来的信息增益。换句话说,就是用后验分布 q 来近似先验分布 p 的时候造成的信息损失。再直白一点,就是衡量不同策略之间的差异性。
p(x),q(x)是离散随机变量X中取值的两个概率分布,则p对q的相对熵计算公式如下:

也可以使用:
![]()
其中H(p,q)代表策略p下的交叉熵,H(p)代表信息熵。所以,相对熵 = 某个策略的交叉熵-信息熵。
相对熵用来衡量 q拟合p的过程中产生的信息损耗,损耗越少,q拟合p也就越好。
需要注意的是,尽管从直觉上相对熵(KL散度)是个度量或距离函数, 但是它实际上并不是一个真正的度量或距离。因为KL散度不具有对称性:从分布P到Q的距离通常并不等于从Q到P的距离。 另外D(p||q)必然大于等于0
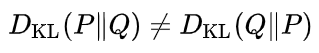
4.5.互信息(Mutual Information)
互信息用来表示两个变量X与Y之间是否有关系,以及关系的强弱。
用公式可以表示为:
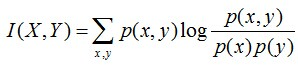
通过公式的计算,可得变量X与Y的互信息就是信息熵H(X)与条件熵H(X|Y)的差: I(X,Y)=H(X)-H(X|Y)=H(X) + H(Y) - H(X,Y)
参考:
https://blog.csdn.net/qq_39521554/article/details/80559531
https://baijiahao.baidu.com/s?id=1615832462981347284&wfr=spider&for=pc
https://www.cnblogs.com/wkang/p/10068475.html