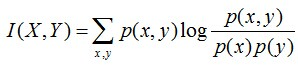ℹ️ 本文参考自 [d2l] Information Theory

此外，本文所提到的 $\log (\cdot )$ 如无特殊说明均指 ${\log }_2(\cdot )$。

一、自信息（Self-information）

先来看一个例子。掷一个质地均匀的骰子，会有 $6$ 种可能的结果，且每种结果发生的概率均为 $1/6$。现在：

• 设事件 X = { 点数不大于 6 } X=\{\text{点数不大于}6\} X={点数不大于6}，则显然 $\mathbb{P}(X)=1$；此外，这句话是废话，它并没有告诉我们任何信息，因为掷一个骰子得到的点数肯定不会超过 $6$；
• 设事件 X = { 点数不大于 5 } X=\{\text{点数不大于}5\} X={点数不大于5}，则显然 $\mathbb{P}(X)=5/6$；此外，这句话包含了一些信息，但并不多，因为我们差不多能够猜到结果；
• 设事件 X = { 点数正好等于 2 } X=\{\text{点数正好等于}2\} X={点数正好等于2}，则显然 $\mathbb{P}(X)=1/6$；此外，这句话的信息量要比上面那句话更大，因为 { 点数正好等于 2 } \{\text{点数正好等于}2\} {点数正好等于2} 包含了 { 点数不大于 5 } \{\text{点数不大于}5\} {点数不大于5} 的信息在里面。

从这个例子可以看出，一个事件 $X$ 所包含的信息量和它发生的概率有关系。概率越小信息量越大，概率越大信息量越少。

设事件 $X$ 所包含的信息量为 $I(X)$，其发生的概率为 $p\triangleq \mathbb{P}(X)$，那么我们如何寻找 $I(X)$ 与 $p$ 之间的关系呢？

首先，我们有以下常识：

• 观测一个几乎确定的事件得到的信息量几乎是 $0$；
• 共同观测两个随机变量得到的信息量不超过分别观测两个随机变量得到的信息量的和，且该不等式取等当且仅当两个随机变量相互独立。

设事件 X = { A 与 B 同时发生，其中 A 、 B 相互独立 } X=\{A与B同时发生，其中A、B相互独立\} X={A与B同时发生，其中A、B相互独立}，则显然 $\mathbb{P}(X)=\mathbb{P}(A)\mathbb{P}(B)$，而根据上述常识，又有 $I(X)=I(A)+I(B)$。不妨设 $I(\ast )=f(\mathbb{P}(\ast ))$，则

$$f(\mathbb{P}(A)\cdot \mathbb{P}(B))=f(\mathbb{P}(X))=I(X)=I(A)+I(B)=f(\mathbb{P}(A))+f(\mathbb{P}(B))$$

不难看出 $\log (\cdot )$ 能够满足这一要求。但考虑到 $\log x$ 在 $(0,1]$ 上是非正的且单调递增，所以我们一般采用 $-\log (\cdot )$ 来衡量一个事件的信息量。

综合以上，设事件 $X$ 发生的概率为 $p$，则其信息量（又称自信息）可以这样计算：

$$I(X)=-\log p\text{\hspace{1em}(1)}$$

---

• 当 $(1)$ 式中的 $\log$ 以 $2$ 为底时，自信息的单位是 $\text{bit}$；
• 当 $(1)$ 式中的 $\log$ 以 $e$ 为底时，自信息的单位是 $\text{nat}$；
• 当 $(1)$ 式中的 $\log$ 以 $10$ 为底时，自信息的单位是 $\text{hart}$。

还可以得到：

$$1\text{nat}={\log }_{2}e\text{bit}\approx 1.443\text{bit},1\text{hart}={\log }_{2}10\text{bit}\approx 3.322\text{bit}$$

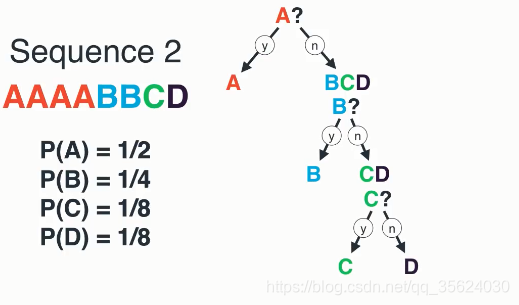
我们知道，对于任何长度为 $n$ 的二进制序列，它包含 $n$ 比特的信息。例如，对于序列 $0010$，它出现的概率是 $1/2^4$，因此

$$I(\text{“0010”})=-\log \frac{1}{2^4}=4\text{bits}$$

二、熵（Entropy）

设随机变量 $X$ 服从分布 $\mathcal{D}$，则 $X$ 的熵定义为其信息量的期望：

$$H(X)={\mathbb{E}}_{X\sim \mathcal{D}}[I(X)]\text{\hspace{1em}(2)}$$

若 $X$ 是离散分布，则

$$H(X)=-{\mathbb{E}}_{X\sim \mathcal{D}}[\log p_i]=-\sum _i{p}_i\log p_i$$

若 $X$ 是连续分布，则

$$H(X)=-{\mathbb{E}}_{X\sim \mathcal{D}}[\log p(x)]=-\int p(x)\log p(x)\text{d}x$$

在离散情况下，设 $X$ 只取 $k$ 个值，则有：$0\le H(X)\le \log k$。

📌 与信息量不同的是，这里的 $X$ 是随机变量而不是事件
📌 把事件看成一个点，则信息量可以看成一个点所产生的的信息，而信息熵则代表一系列点所产生的信息的均量
📌 接下来的章节中我们都将只讨论离散情形，连续情形下的公式可类比推理

2.1 联合熵（Joint Entropy）

我们已经知道如何计算 $X$ 的信息熵了，那么如何计算 $(X,Y)$ 的信息熵呢？

设 $(X,Y)\sim \mathcal{D}$，联合概率分布为 $p_{ij}\triangleq \mathbb{P}(X=x_i,Y=y_j)$，再记 $p_i=\mathbb{P}(X=x_i),p_j=\mathbb{P}(Y=y_j)$，依照信息熵的定义类似可得

$$H(X,Y)=-\sum _{ij}{p}_{ij}\log p_{ij}\text{\hspace{1em}(3)}$$

如果 $X=Y$，则 $H(X,Y)=H(X)=H(Y)$；如果 $X$ 和 $Y$ 相互独立，则 $p_{ij}=p_i\cdot p_j$，进而

$$H(X,Y)=-\sum _{ij}(p_i\cdot p_j)(\log p_i+\log p_j)=-\sum _j{p}_j\sum _i{p}_i\log p_i-\sum _i{p}_i\sum _j{p}_j\log p_j=H(X)+H(Y)$$

此外，总有以下不等式成立：

$$H(X),H(Y)\le H(X,Y)\le H(X)+H(Y)$$

2.2 条件熵（Conditional Entropy）

条件熵 $H(Y|X)$ 表示在已知随机变量 $X$ 的情况下随机变量 $Y$ 的不确定性，定义为 $X$ 给定条件下 $Y$ 的条件概率分布的熵对 $X$ 的数学期望：

$$H(Y|X)=\sum _i{p}_{i}H(Y|X=x_i)=\sum _i{p}_i\left(-\sum _j{p}_{j|i}\log p_{j|i}\right)=-\sum _{ij}{p}_{ij}\log p_{j|i}\text{\hspace{1em}(4)}$$

利用 $p_{j|i}=p_{ij}/p_i$ 可得

$$H(Y|X)=H(X,Y)-H(X)$$

从上式可以看出，$H(Y|X)$ 实际上代表了包含在 $Y$ 但不包含在 $X$ 中的信息（类似于 $\mathbb{P}(B\backslash A)=\mathbb{P}(A\cup B)-\mathbb{P}(A)$）。

2.3 互信息（Mutual Information）

给定随机变量 $(X,Y)$，我们已经知道了 $X$ 的信息可以用 $H(X)$ 来表示；$(X,Y)$ 总共的信息可以用 $H(X,Y)$ 来表示；包含在 $Y$ 但不包含在 $X$ 中的信息可以用 $H(Y|X)$ 来表示。那我们该用什么来衡量 $X$ 和 $Y$ 都包含的信息呢？

答案是互信息，其定义如下（可以理解为集合 $X$ 与 $Y$ 的交集）：

$$I(X,Y)=H(X,Y)-H(Y|X)-H(X|Y)\text{\hspace{1em}(5)}$$

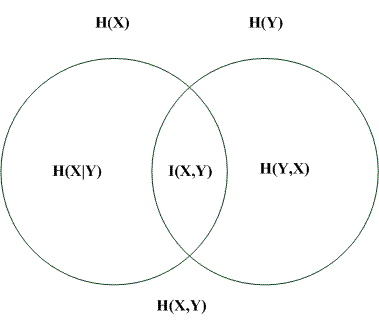
熵、联合熵、条件熵、互信息之间的关系如下：

从上图还可以得到：

$$\begin{array}{rl}I(X,Y)& =H(X)-H(X|Y)\\ I(X,Y)& =H(Y)-H(Y|X)\\ I(X,Y)& =H(X)+H(Y)-H(X,Y)\end{array}$$

我们将 $(5)$ 式展开得到

$$\begin{array}{rl}I(X,Y)& =-\sum _{ij}{p}_{ij}\log p_{ij}+\sum _{ij}{p}_{ij}\log p_{j|i}+\sum _{ij}{p}_{ij}\log p_{i|j}\\ & =\sum _{ij}{p}_{ij}(\log p_{j|i}+\log p_{i|j}-\log p_{ij})\\ & =\sum _{ij}{p}_{ij}\log \frac{p_{ij}}{p_i\cdot p_j}\\ & ={\mathbb{E}}_{(X,Y)\sim \mathcal{D}}\left[\log \frac{p_{ij}}{p_i\cdot p_j}\right]\end{array}$$

互信息的一些性质：

• 对称性：$I(X,Y)=I(Y,X)$；
• 非负性：$I(X,Y)\ge 0$；
• $I(X,Y)=0$ $\iff$ $X$ 与 $Y$ 相互独立；

2.4 点互信息（Pointwise Mutual Information）

点互信息定义为：

$$\text{PMI}(x_i,y_j)=\log \frac{p_{ij}}{p_i\cdot p_j}\text{\hspace{1em}(6)}$$

结合 2.3 节，我们会发现有如下关系成立（好比信息熵是信息量的期望一样，互信息也是点互信息的期望）

$$I(X,Y)={\mathbb{E}}_{(X,Y)\sim \mathcal{D}}\left[\text{PMI}(x_i,y_j)\right]$$

PMI 的值越高，表示 $x_i$ 与 $y_j$ 的相关性越强。PMI 常用于 NLP 任务中计算两个单词之间的相关性，但如果语料库不足，可能会出现 $p_{ij}=0$ 的情况，这就导致两个单词的互信息为 $-\infty$，因此需要做一个修正：

$$\text{PPMI}(x_i,y_j)=\max (0,\text{PMI}(x_i,y_j))$$

上述的 PPMI 又称为正点互信息（Positive PMI）。

三、相对熵（KL散度）

相对熵（Relative Entropy）又称为KL散度（Kullback–Leibler divergence），后者是其更常用的名字。

设随机变量 $X$ 服从概率分布 $P$，现在我们尝试用另外一个概率分布 $Q$ 来估计 $P$（假设 $Y\sim Q$）。记 $p_i=\mathbb{P}(X=x_i),q_i=\mathbb{P}(Y=x_i)$，则KL散度定义为

$$D_{\text{KL}}(P\Vert Q)={\mathbb{E}}_{X\sim P}\left[\log \frac{p_i}{q_i}\right]=\sum _i{p}_i\log \frac{p_i}{q_i}\text{\hspace{1em}(7)}$$

KL散度的一些性质：

• 非对称性：$D_{\text{KL}}(P\Vert Q)\ne D_{\text{KL}}(Q\Vert P)$；
• 非负性：$D_{\text{KL}}(P\Vert Q)\ge 0$，等式成立当且仅当 $P=Q$；
• 若存在 $x_i$ 使得 $p_i>0,q_i=0$，则 $D_{\text{KL}}(P\Vert Q)=\infty$。

KL散度被用来衡量两个概率分布之间的差异。如果两个分布完全相等，则KL散度为 $0$。因此，KL散度可以用作多分类任务的损失函数。

📌 由于KL散度不满足对称性，因此它不是严格意义上的 “距离”

四、交叉熵（Cross-Entropy）

我们将 $(7)$ 式拆解

$$D_{\text{KL}}(P\Vert Q)=\sum _i{p}_i\log p_i-\sum _i{p}_i\log q_i$$

若令 $\text{CE}(P,Q)=-{\sum }_i{p}_i\log q_i$，则上式可写成

$$D_{\text{KL}}(P\Vert Q)=\text{CE}(P,Q)-H(P)$$

而 $\text{CE}(P,Q)$ 就是我们所说的交叉熵，其正式定义为

$$\text{CE}(P,Q)=-{\mathbb{E}}_{X\sim P}[\log q_i]\text{\hspace{1em}(8)}$$

结合KL散度的非负性，我们还可以得到 $\text{CE}(P,Q)\ge H(P)$，该不等式又称为吉布斯不等式。

📌 通常 $\text{CE}(P,Q)$ 也会写成 $H(P,Q)$

---

交叉熵计算一例：

$P$ 是真实分布，而 $Q$ 是估计分布，考虑三分类问题，对于某个样本，其真实标签和预测结果列在下表中：

	类别 1	类别 2	类别 3
target	0	1	0
prediction	0.2	0.7	0.1

从上表可以看出，该样本真实情况是属于类别 2，且 $p_1=0,p_2=1,p_3=0,q_1=0.2,q_2=0.7,q_3=0.1$。

因此

$$\text{CE}(P,Q)=-(0\cdot \log 0.2+1\cdot \log 0.7+0\cdot \log 0.1)=-\log 0.7\approx 0.5146$$

📶 当给定了数据集，$H(P)$ 就成了一个常数，因此KL散度和交叉熵都能够用作多分类问题的损失函数。当真实分布 $P$ 是 One-Hot 向量时，则有 $H(P)=0$，此时交叉熵等于KL散度

4.1 二元交叉熵（Binary Cross-Entropy）

二元交叉熵（BCE）是交叉熵的一个特例

$$\begin{array}{rl}\text{BCE}(P,Q)& =-\sum _{i=1}^2{p}_i\log q_i\\ & =-(p_1\log q_1+p_2\log q_2)\\ & =-(p_1\log q_1+(1-p_1)\log (1-q_1))\end{array}$$

BCE 可用作二分类或多标签分类的损失函数。

📌 交叉熵损失前通常接Softmax，而二元交叉熵损失前通常接Sigmoid
📌 二分类情景下，输出层既可以采用一个神经元+Sigmoid也可以采用两个神经元+Softmax，两者等价，但使用前者训练起来更快一些

BCE 还可通过 MLE 得到。给定 $n$ 个样本：$x_1,x_2,\cdots ,x_n$，每个样本的标签 $y_i$ 非 $0$ 即 $1$（$1$ 代表正类，$0$ 代表负类），神经网络的参数简记为 $\theta$。我们的目标是寻找最优的 $\theta$ 使得 ${\hat{y}}_i={\mathbb{P}}_{\theta }(y_i|x_i)$。设 $x_i$ 被分类为正类的概率为 ${\pi }_i={\mathbb{P}}_{\theta }(y_i=1|x_i)$，则对数似然函数为

$$\begin{array}{rl}\ell (\theta )& =\log L(\theta )\\ & =\log \prod _{i=1}^n{\pi }_i^{y_i}(1-{\pi }_i{)}^{1-y_i}\\ & =\sum _{i=1}^n{y}_i\log {\pi }_i+(1-y_i)\log (1-{\pi }_i)\end{array}$$

最大化 $\ell (\theta )$ 等价于最小化 $-\ell (\theta )$，而后者就是二元交叉熵损失。