集合

子集关系

证明A是B的子集
证明A中任意的元素都在B中即可

句式

For each element a in set A， we have a belongs to B. So A is the subset of B.
（以下我都尽量用符号吧，毕竟符号更直观点）

两个集合相等

证明A=B
证明A,B互为子集即可

句式

For each element a in set A, 
……（题目条件）
we have a∈B, i.e A ⊆ B.
For each element a in set B,
……（题目条件）we have a∈A, i.e B ⊆ A.
To sum up, A=B holds obviously.

例子

A,B,C是非空有限集，证明A-（B∪C）=（A-B）∩（A-C）

Proof:
∀ x∈A-（B∪C）, we have x∈A and x∉B∪C，which indicates x∉B and x∉C. So x∈A-B and x∈A-C hold obviously, i.e x∈（A-B）∩（A-C）holds. Now we can say A-（B∪C）⊆（A-B）∩（A-C）
∀ x∈（A-B）∩（A-C）, we have x∈（A-B）and x∈（A-C），which indicates x∈A, x∉B and x∉C, i.e x∈A-（B∪C）holds. Now we can say （A-B）∩（A-C）⊆A-（B∪C）.
To sum up, A-（B∪C）=（A-B）∩（A-C）.
——————————————————————

令R为从A到B的二元关系，S为从B到C的二元关系，若D是A的一个子集，证明(S○R)(D) = S(R(D))

Suppose that z∈C exists in (S○R)(D), there is a element x∈D that makes x(S○R)z holds.
By the definition of composite, there must be y∈D, so we have xRy and ySz hold, which implies y∈R(x) and z∈S(y) so that z∈S(R(x)).
Since x∈D and z∈(S○R)(D) hold, we have z∈S(R(D)), i.e (S○R)(D) ⊆ S(R(D)) holds.

∀ z∈S(R(D)) there must be a y∈B that makes z∈S(y) hold. There must exists x∈D making xRy holds, i.e y∈R(x) and z∈S(y) hold obviously, which makes z∈(S○R)(x) hold.
Since x∈D hold, now we can say that z∈(S○R)(D), i.e S(R(D)) ⊆ (S○R)(D) holds.
To sum up, (S○R)(D) = S(R(D)).
——————————————————————

设A，B是集合，定义 （环积）运算，如A⊗B = （A⊕B）
证明A⊗B=（A∪B ）∩（A∪B）
（上划线我实在找不到表示方法，就用斜杠表示吧，遇到双重的，我内层就以补集符号∁代替了，意为取反；⊕是异或运算）

Proof：
A⊗B=（A⊕B） 题目条件
=（∁A∩B ∪ A∩∁B） 根据⊕定义
=(∁A∩B) ∩ (A∩∁B) 德·摩根定律
=(∁A ∪ B) ∩ (A ∪ ∁B) 德·摩根定律
=(A∪B)∩(A∪B) 化简得

划分（partition）

非空集合A的非空子集（在划分中称为block或者cell）组成的集合，就是A的划分。
比如下图a11~a93为A中的全部元素，其子集如有颜色部分所示
这些子集共同组成了一个A的划分

其满足：
1、A中每个元素属于划分中的某个集合
2、如果A₁、A₂是A中的不同元素，那么A₁∩A₂=Ø

补充：A的幂集是A所有子集构成的集合，所以划分（没有空集元素）是幂集的子集

句式

Supposing ∀ a∈A，∃b∈B,
……（题目条件）
a∈b holds.
Suppose that A₁、A₂∈B and A₁≠A₂ 
……（题目条件）
A₁∩A₂ = Ø holds.
To sum up, B is the partition of A.

例子

设π={Ai：i∈I}（I在离散数学中代表整数集）是集合A上的的一个划分，证明对于任意的集合B，所有Ai∩B≠Ø的Ai∩B组成的集合是A∩B的划分。

Proof:
We define S as a set that made of {Ai∩B, Ai∩B≠Ø and i∈I}
Supposing ∀ a∈A∩B, there exists a set b∈S that contains the element a since b = {Ai∩B} and s=A∩B={Ai∩B,i∈I}, i.e a∈b holds.
Suppose that s₁、s₂∈B, which are made of different Ai∩B. By the definition of partition, Ai≠Aj holds, if i≠j, i.e s₁∩s₂=Ø.
To sum up, S that is made of {Ai∩B, Ai∩B≠Ø and i∈I} is the partition of A∩B.

关系

关系R的自反性（reflexive）反自反（irreflexive）

三者关系如下

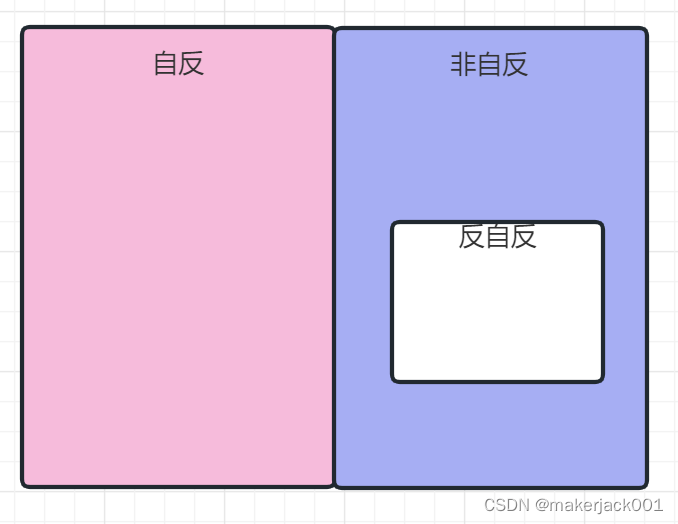
对A中任意元素a，都有（a,a）∈R，那么R就具备自反性
如果都不在那就反自反，存在（a,a）∉R 就是非自反，反自反是特殊的非自反

句式

For each element a∈A, ……（这里是题目给的条件，比如A×A什么的）, 
1  we have (a,a) ∈ R, i.e R is reflexive.
2  we have (a,a) ∉ R, i.e R is irreflexive

关系R的对称性（symmetric）反对称（antisymmetric）

三者关系如下

任意的a,b∈A，都有（a,b）∈R 并且（b.a）∈R ,那么R就具备对称性
如果都有（a,b）∈R并且（b,a）∉R,那么R就具备反对称
存在（a,b）∈R并且（b,a）∉R 就是斜对称，反对称是特殊的斜对称

句式

For each a,b are the elements in A, ……（题目条件）
1  we have (a,b) ∈R and (b,a) ∈R，i.e R is symmetric
2  we have (a,b) ∈R， (b,a) ∈R and a=b, i.e R is antisymmetric

例子

证明若集合A上的一个二元关系R是对称的，则对于任意的n≥1，Rⁿ也是对称的

Proof：（数学归纳法，其应用往往在于前后条件成立有因果关系时，即k成立能推导k+1成立，此时应用数学归纳法）

1. By the condition, when n = 1, R is symmetric.
2. When n ＞ 1, supposing R^k is symmetric, ∀(a,b)∈R^k, there exists c∈A for (a,c)∈R^k and (c,b)∈R holding. Moreover, R^k and R is symmetric, which indicate (c,a)∈R^k and (b,c)∈R hold obviously. Since R^k+1 = R^kR holds, (b,a) ∈R^k+1 holds obviously, which suggests R^k+1 is Symmetric.

To sum up, Rⁿ is symmetric for ∀ n ≥ 1.

关系R的传递性（transitive）

（a,b）∈R ，（b,c）∈R
如果有（a,c）∈R，那么R就具有传递性

句式

For each (a,b) ∈R and (b,c) ∈R, ……（题目条件）
we have (a,c) ∈ R, i.e R is transitive

例子

设R∈A×A，对于任意的x,y,z∈A，如果（x,y）∈R且（y，z）∈R那么（z，x）∈R，则称R为A上的循环关系，证明若R是自反和循环的，则R具有对称性和传递性。

Proof:
Supposing a,b∈A and (a,b)∈R, since R is reflexive, (a,a)∈R holds. By the condition, (a,a)∈R and (a,b)∈R so (b,a)∈R holds obviously, i.e R is symmetric.
Basing on the condition, ∀a,b,c∈R, if (a,b)∈R and (b,c)∈R, (c,a)∈R holds. Since R is Symmetric, (a,c)∈R holds, i.e R is transitive.

关系R的相容性（compatible）

R具有自反性，对称性，不必具备传递性（所以等价关系是特殊的相容关系）
依次证明自反性、对称性即可

句式

……
R is reflexive.
……
R is symmetric.
To sum up, R is compatible relation.

例子

集合A的覆盖为{A₁,A₂,A₃,……An}，证明R=A₁×A₁∪A₂×A₂……An ×An是相容关系

Proof:
For ∀ a∈A, by the definition that {A₁,A₂,A₃,……An} is the covering of A, we konw taht a∈A₁∪A₂∪A₃∪……An, which indicates (a,a)∈A₁×A₁∪A₂×A₂∪A₃×A₃∪……An×An
Since R=A₁×A₁∪A₂×A₂∪A₃×A₃∪……An×An, i.e R is reflexive.
For ∀ a,b∈A, by the condition, we know that there exists A_i for a,b∈A_i holding. Furthermore, (a,b)∈A_i×A_i and (b,a)∈A_i×A_i hold obviously, which implies that (a,b)∈A₁×A₁∪A₂×A₂∪A₃×A₃∪……An×An and (b,a)∈A₁×A₁∪A₂×A₂∪A₃×A₃∪……An×An, i.e R is symmetric.
To sum up, R is compatible.

关系R的等价性（equivalent）

先证明R的自反性，再证对称性，最后证传递性
总结一下就是全等关系

句式

……
R is reflexive.
……
R is symmetric.
……
R is transitive.
To sum up, R is equivalence relation.

偏序关系（partial order）

关系R满足自反性、反对称、传递性，其就是偏序关系

句式

……
R is reflexive.
……
R is antisymmetric.
……
R is transitive.
To sum up, R is partial order.

格（lattices）

任意两个元素都有最大下边界和最小上边界的偏序集（其关系是偏序关系）就是格

句式

……
A is a poset.
……
∀ a,b∈A 
x is the greatest lower bound of a and b.
……
y is the least upper bound of a and b.
To sum up, A is a lattice

例子

令L为一个格，对于L中的任意两个元素a和b，证明下列结论：
（1）a∨b=b，当且仅当a≤b
（2）a∧b=a，当且仅当a≤b

Proof：

1. =>
   By the definition of LUB, we have a≤a∨b. Basing on the condition, it is clear that a∨b = b, i.e a≤b holds obviously.
   <=
   Since a≤b and b≤b, we have b is one of the upper bound of a and b. By the definition of LUB, we have a∨b≤b. However, a∨b is one of the upper bound of a and b, which implies b≤a∨b., i.e a∨b=b holds obviously.
2. =>
   By the definition of GLB, we have a∧b≤b. Basing on the condition, it is clear that a∧b = a, i.e a≤b holds obviously.
   <=
   Since a≤a and a≤b, we have a is one of the lower bound of a and b. By the definition of GLB, we have a≤a∧b. However, a∧b is one of the lower bound of a and b, which suggests a∧b≤a., i.e a∧b=a holds obviously.
   ——————————————

证明（p（x），⊆）是格，其中p（x）是集合x的幂集
Proof:
∀ a∈p（x），it is clear that a⊆a holds obviously, i.e ⊆ is reflexive.
Supposing a,b∈p（x）a⊆b and b⊆a, by the definition of ⊆, a=b holds, i.e ⊆ is antisymmetric.
Suppose that a,b,c⊆p（x）,a⊆b and b⊆c. By the definition of ⊆, it is clear that a⊆c, i.e is transitive.
To sum up, ⊆ is partial order reletion, p（x）is a poset.
∀ a,b∈p（x）, we have a∩b⊆a，and a∩b⊆b, which indicates that a∩b is a lower bound of a and b. Supposing c∈p（x）and c⊆a, c⊆b, we obtain c⊆a∩b, i.e a∩b is the greatest lower bound of a and b.
∀ a,b∈p（x）, we have a⊆a∪b and b⊆a∪b, which implies that a∪b is a upper bound of a and b. Supposing c∈p（x）and a⊆c, b⊆c, we obtain a∪b⊆c, i.e a∪b is the least upper bound of a and b.
To sum up, p（x）is a lattice.

引申

格由于其具有的最大下边界GLB 最小上边界LUB，有一些性质，常常会在计算中做文章
用a∧b表示GLB，a∨b表示LUB，其具有一些运算中用到的性质
a∨b=b，当且仅当a≤b
a∧b=a，当且仅当a≤b
幂等律
a∨a=a
a∧a=a
交换性律
a∨b = b∨a
a∧b = b∧a
结合性律
a∨(b∨c) = (a∨b)∨c
a∧(b∧c) = (a∧b)∧c
吸收性律
a∨(a∧b) = a
a∧(a∨b) = a

例子

令（L,≤）是一个分配格，证明如果存在a∈L，使得a∧x=a∧y,并且a∨x=a∨y 那么就有x=y.

Proof:
y≤y∨(a∧y) 这一步有点取巧，为了凑出a，利用LUB性质
=(y∨a)∧(y∨y) 分配律展开
=(a∨y)∧y 幂等律
=(a∨x)∧y 题目条件
=(a∧y)∨(x∧y) 分配律展开
=(a∧x)∨(y∧x) 题目条件，交换律
=(a∨y)∧x 分配率提取x
=(a∨x)∧x 题目条件
≤ x GLB的性质

x≤x∨(a∧x) LUB的性质
=(x∨a)∧(x∨x) 分配率展开
=(y∨a)∧x 题目条件，幂等率
=(y∧x)∨(a∧x) 分配率展开
=(x∧y)∨(a∧y) 交换律，题目条件
=(a∨x)∧y 分配率提取y
=(a∨y)∧y 题目条件
≤y

To sum up, x=y holds.
——————————————————————————
令*是有限集合A上的一个二元运算，若对于∀a,b,c∈A,满足
（1）a = a * a
（2）a * b = b * a
（3）a * （b * c）=（a * b） * c
在A上定义一个关系≤，形如 a ≤ b ⇔ a = a * b，证明
1、（A,≤）是一个偏序集。
2、∀ a,b ∈ A, a ∧ b = a * b

Proof:

1. ∀a∈A, by the condition, we have a * a = a ⇔ a ≤ a, which implies (a,a) ∈ R, i.e R is reflexive.
   Supposing a,b∈A, a ≤ b and b ≤ a, by the condition, we obtain a = a * b and b = b * a.
   Since * is commutative, a = a * b = b * a = b holds obviously, i.e R is antisymmetric.
   Suppose that a,b,c ∈ A and a ≤ b, b ≤ c, which indicate a = a * b and b = b * c, i.e a = a * (b * c) hold obviously. Since * is associative, we have a = (a * b) * c = a * c. Basing on the definition, we have a ≤ c holds, i.e R is transitive.
   To sum up, ≤ is partial order and (A,≤) is a poset.

2. Supposing a * b=a * b * b=(a * b) * b, by the condition we have a * b ≤ b. Similarly a * b=a * a * b=(a * b) * a, Basing on the condition we have a * b≤a. So a * b is a lower bound of a and b. Suppose that c ∈ A, c≤a and c≤b hold, which indicate that c=c * a and c=c * b hold clearly. Furthermore, c=(c * a) * b=c * (a * b) hold obviously. By the condition, c≤a * b hold, i.e a * b is the greatest lower bound of a and b.
   To sum up, ∀ a,b ∈ A, a ∧ b = a * b holds.

群

二元运算（Binary operation）

定义在A上的二元运算满足
处处有定义
运算结果唯一
这两点没法直观证明，直接声明一下即可

句式

& is an everywhere defined function.
only one element of A is assigned to each ordered pair.

幺元（identity）逆元（inverse）

这是二元运算下的特殊元 ，以下的二元运算符都用&表示
幺元 e&x=x&e=x
逆元 x&y=y&x=e

句式

For element e in A, ……  
a*e=e*a=x, e is the identity of Afor each element x in A, there exists y, ……
x*y=y*x=e, A has the inverse.

半群（semigroup）

非空集合A与一个定义在A上的满足结合律的二元运算符&组成的整体（A,&）

句式

A is a nonempty set.
……
& is a binary operation
……
& is associative 
……
（A,&）is a semigroup

拟群（monoid）

半群基础上存在幺元

句式

……
A is a semigroup
……
e is the indentity of A
To sum up, (A,&) is a monoid

群（group）

拟群基础上存在逆元

句式

……
A is a monoid
……
For each x∊A, y is the inverse of x
To sum up, (A,&) is a group

例子

令（S, ○ ）和（T, ○’ ）为两个群，证明（S×T，○’‘）也是一个群，其中 ○‘’运算定义为:
（s₁,t₁）○’'（s₂,t₂）=（s₁○s₂ ,t₁○’t₂ ）

Proof
By the condition, it is clear that S×T is a nonempty set and ○’’ is a binary operation.
∀ s₁,s₂ ,s₃ ∈ S and t₁,t₂ ,t₃ ∈ T, we have
(s₁,t₁) ○’’ (s₂,t₂)○’‘(s₃,t₃) = （s₁○s₂ ,t₁○’t₂ ）○’’ (s₃,t₃) = (s₁○s₂○s₃,t₁○’t₂○’t₃) and
(s₁,t₁) ○’‘[ (s₂,t₂)○’‘(s₃,t₃)] = (s₁,t₁) ○’‘(s₂○s₃,t₂ ○’t₃) = (s₁○s₂○s₃,t₁○’t₂○’t₃) hold.
To sum up, ○’’ is associative, which implies（S×T，○’'） is a semigroup.
What is more, Since （S, ○ ）and（T, ○’ ）are groups, there must be two identity e₁∈S and e₂∈T, for each element s∈S and t∈T, making s ○ e₁ = e₁ ○ s = s and t ○’ e₂ = e₂ ○’ t = t hold.
By the condition, (s,t) ○’’ (e₁,e₂ ) = (s ○ e₁, t ○’ e₂ ) = (e₁ ○ s, e₂ ○’ t) = (s,t) holds obviously, i.e (e₁,e₂) is the identity of (S×T,○’‘), which suggests (S×T,○’') is a monoid.
Moreover, Since （S, ○ ）and（T, ○’ ）are groups, they should have inverses x,y for each element s∈S or t∈T making s○x = x○s = e₁ and y○’t = t○’y = e₂ hold.
Basing on the condition, (s,t) ○’’ (x,y) = (s ○ x,t ○’ y) = (x ○ s,y ○’ t) = (e₁,e₂) hold obviously, i.e for each (s,t) in S×T, (x,y) is inverse of (s,t).
To sum up, (S×T,○’') is a group.

交换群（Abelian group）

群基础上二元运算&满足交换律

句式

……
A is a group
……
& is commutative
A is a Abelian group

例子

在整数集合Z上定义0运算，如∀ x,y∈Z，x0y=x+y-2，证明（Z,0）是交换群

Proof:
It is clear that Z is a nonempty set.
By the condition 0 is a everywhere defined function and only one element of A is assigned to each ordered pair.
Supposing a,b,c∈Z, and (a0b)0c = (a+b-2)0c = (a+b-2)+c-2=a+b+c-4 holds.
Moreover a0(b0c) = a0(b+c-2) = a+(b+c-2)-2 = a+b+c-4 holds obviously, **i.e 0 is associative, which indicates that (Z,0) is a semigroup. **What’s more, for each x,2∈Z, we have x02 = x+2-2 = x and 20x = 2+x-2 = x, i.e x02=20x=2, so 2 is the identity of A. which implies (Z,0) is a monoid.
∀ x∈Z, we have 4-x ∈Z, x0(4-x) = x+(4-x)-2 = 2 and (4-x)0x = (4-x)+x-2 = 2 hold obviously, i.e 4-x is the inverse of x for each x ∈ Z, which implies (Z,0) is a group.
∀ a,b∈Z, we have a0b = a+b-2 and b0a = b+a-2, i.e a0b = b0a, which suggests that 0 is commutative.
To sum up, (Z,0) is an Abelian group.

特别鸣谢

某位头像美腻的小姐姐一直帮助我不断修正，方有此文。