1.kruskal
设图共有k个顶点
当k=2时,图G只有一条边,显然最短边为此边,图G的最小生成树为其自身。
设k=n时,成立。
对于有n+1个顶点的图G,接最短边e后,剩余n个顶点待连接,由假设,成立,那么其最小生成树为T’。
反证法:若T’不是G的最小生成树,则应存在含e的最小生成树T*,则对T短接e,G’生成树T-{e},则此时有
W(T*-{e})=W(T*)-W{e}<W(T)-W{e}=W(T’)
与T’是G的最小生成树相矛盾,故T*不存在,T就是G的最小生成树
2.Prim
反证法
假设权值最小的边不在最小生成树T中,此时将权值最小的边加入T中,必然构成回路,去除回路中权值最大的边,新的生成树T’权值比T的权值小,故最小生成边必然在最小生成树中。
3.由栈的特性,不存在i<j<k,使得pj<pk<pi
反证法
假设存在i<j<k,使得pj<pk<pi,因为原序列1,2,3…n是单调递增序列,
又pi>pk,pi>pj,故pk pj必然在1,2,3…pi-1的序列中。
同理可得,pk>pj,pj必在1…pk-1的序列中,综上,分部序列应该为:1,…pj…pk…pi…n
那么出栈的时候要求i<j<k,i最小,pi最先出栈,1,…pj…pk…pi都应先入栈,pi出栈后,pk必比pj先出栈,即出栈顺序应为:pi pk pj 根据序列的单调性,下标序列应为i<k<j,与假设矛盾,故原命题得证。
4.Dijkstra


5.Floyd


6.Huffman最优性
7.前 后序 层次+中序分别确定唯一二叉树
证明题(考研)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/55259.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
离散数学中 集合、关系、群 的证明方法(英文证明附例题)
文章目录 集合子集关系句式 两个集合相等句式例子 划分(partition)句式例子 关系关系R的自反性(reflexive)反自反(irreflexive)句式 关系R的对称性(symmetric)反对称(ant…
中值定理证明题解题思路
对于只有一个未知量的,通常是把未知量替换为x。令等式一边为0,然后把另一边当作F(x),然后找原函数。在写解题过程时,不写如何求得F(x)的,直接设F(x),然后证明F(x)符合某一种中值定理。 例1:f(x)…
回忆当年高考的一道数学证明题
恰逢高考季,昨夜又做梦,与高中相关,就索性来写一篇,题目自定,立意自选。 每年高考后,我都会拿湖北高考的数学试卷做一下,这也许是特殊的爱好吧。知识点和公式基本没有忘记,熟练度肯定…
【期权系列】顶部和底部信号:期权看跌看涨比(PCR)
【期权系列】顶部和底部信号:期权看跌看涨比(PCR) 本篇文章是基于研究报告的复现作品,旨在记录个人的学习过程和复现过程中的一些思路。
感谢华福证券研究员前辈的宝贵思路。 一、期权看跌看涨比(PCR: PutCallRatio&a…
“风口猪”指标-寻找大牛股的波段机会
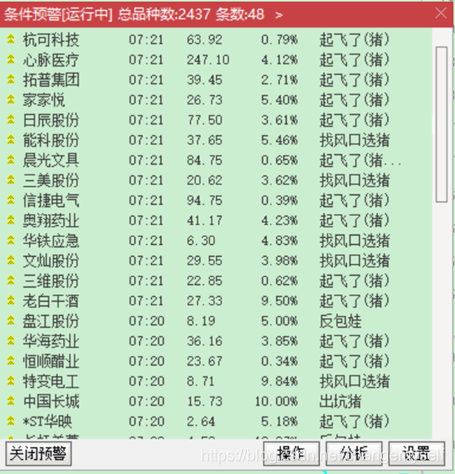
1. “风口猪”指标简介和用法: 为了抓住大牛股的波段行情,买在行情启动阶段,先找到风口,就可以看到猪飞起来了! 4根均线:MA5,MA10是短线,MA60和MA250是长线、 主图指标上有 买入&…
c 语言编写的一元二次方程的根,C#程式求一元二次方程根
C#程式求一元二次方程根以下文字资料是由(历史新知网www.lishixinzhi.com)小编为大家搜集整理后发布的内容,让我们赶快一起来看一下吧! C#程式求一元二次方程根, c# 由使用者输入a,b,c求一元二次方程根的程式 public static void Main() {double a, b, c; Console.Write(&quo…
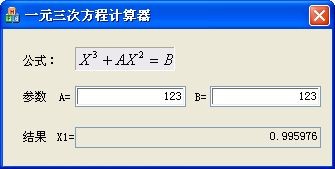
怎么用计算机算一元三次方程,一元三次方程计算器求解(附使用方法)
一元三次方程计算器是一款十分好用的方程计算软件,该软件采用牛顿迭代法计算,用户输入参数A和B就可得出X的值了,还可计算复数根,软件操作简单,十分好用,需要的朋友赶紧来本站下载吧! 一元三次方…
一元线性回归方程C语言实现
之前没写对,尴尬,于是重新研究了一遍,啊,确实没写对大佬帮改了一下
首先来看看如何求线性回归方程公式http://www.gaosan.com/gaokao/263926.html
第一:用所给样本求出两个相关变量的(算术)平均值
第二&…
接口测试用例生成工具介绍及应用
背景
目前,接口测试是开展项目测试实施过程中非常重要的环节,对于新增接口和修改接口更是需要做到应测必测,但是在实施过程中普遍存在一些问题,经分析总结如下:
1.耗时长: 接口测试整体流程较长ÿ…
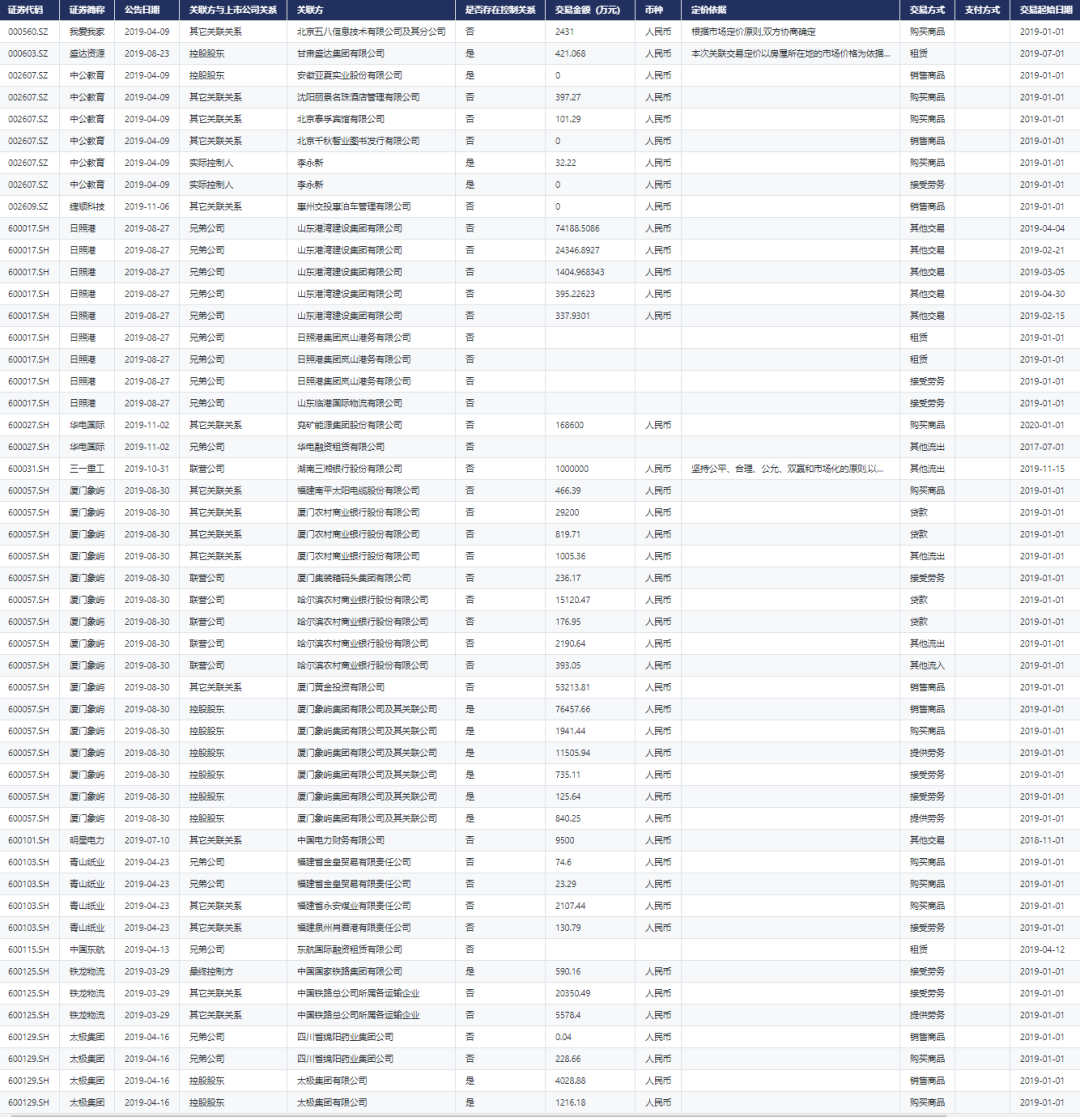
CnOpenData·A股上市公司关联交易数据
一、数据简介 据《上市公司信息披露管理办法》,上市公司作为信息披露义务人,应真实、准确、及时、完整地向市场公开依法及自愿披露的信息。这些公开披露的信息包含但不仅限于公司基本情况、主要会计数据和财务指标、股东持股情况、高管薪酬情况等。上市公…
利用tushare实现选股
ID:399899 量化交易中,首先要弄好的就是选股。然后在才是买卖策略的制定。
不同类型的策略,选股思路也不相同。俗话说得好,不管黑猫白猫,抓到老鼠的就是好猫。一个好的选股策略,往往在量化中是起较为关键的作用的。
…
腾讯微信附近推广告推广,店铺周围黄金3-5公里推广,微信朋友圈广告
继朋友圈广告后,微信4年以来终于推出的第二项广告服务“附近推”——微信终究还是对朋友圈资源下手了。
背靠微信的10亿日活,朋友圈一直以来都是一个巨大广告流量入口,这也是朋友圈广告发展至今依然处于红利期的原因之一。
一:微…
腾讯广点通广告投放-转化归因API回传接口对接踩坑指南
对于腾讯广点通广告平台的文档,实在是忍不住要吐槽一番。本来接收到回传接口文档,看到给的PDF文档没有备注说明,但是看到回传方式,挺简单的。以为一下就能搞定了,但是对接下来才发现,各个字段根本不知道什么…
在 GitHub 上“搞事”,Meta 开源 ImageBind 新模型,超越 GPT-4,对齐文本、音频等 6 种模态!...
整理 | 屠敏 出品 | CSDN(ID:CSDNnews) 据外媒报道,上周四,Google、微软、OpenAI 几家公司的 CEO 受邀去白宫,共论关于人工智能发展的一些重要问题。然而,让人有些想不通的是,深耕 A…
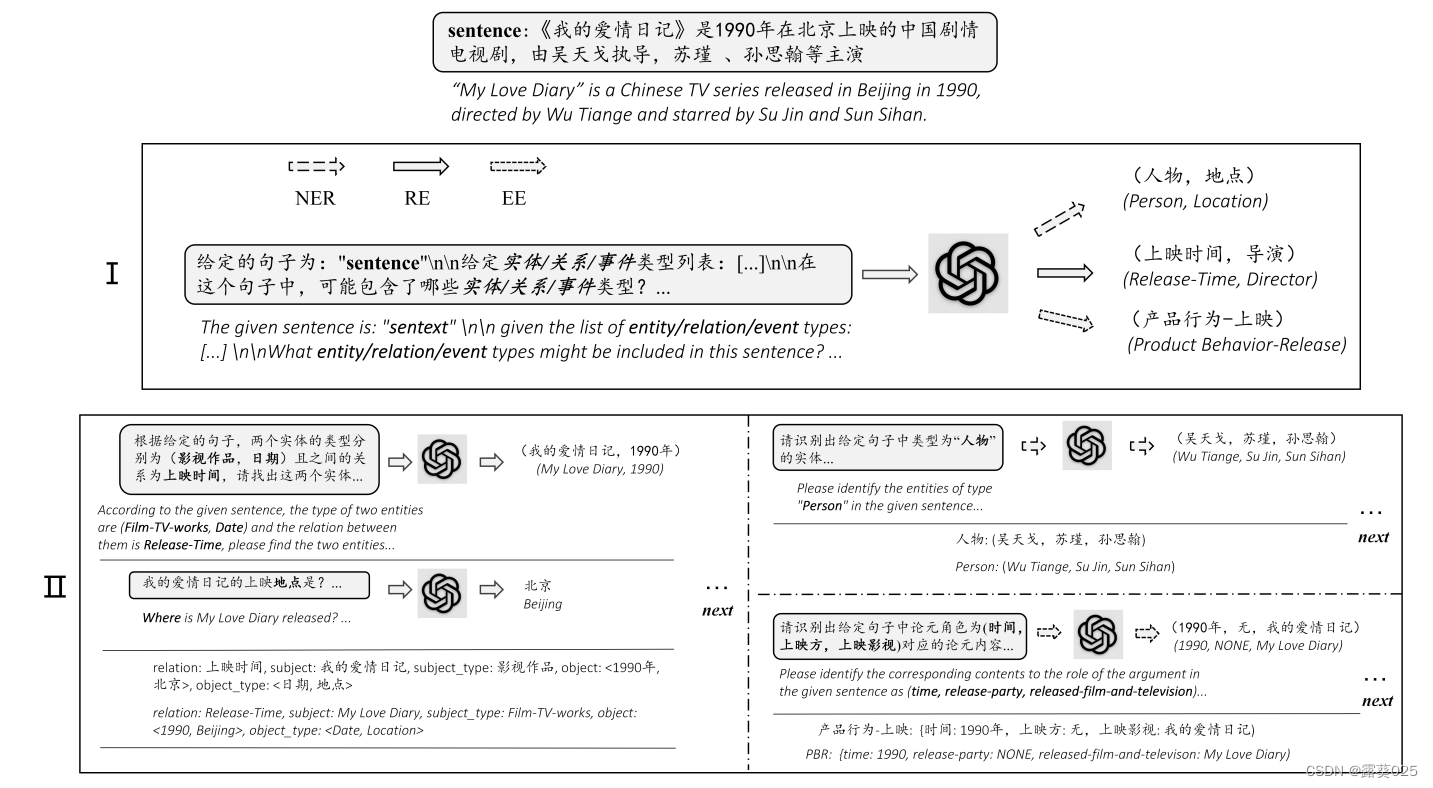
基于ChatGPT聊天的零样本信息提取7.25
基于ChatGPT聊天的零样本信息提取 摘要介绍ChatIE用于零样本IE的多轮 QA 实验总结 摘要
零样本信息提取(IE)旨在从未注释的文本中构建IE系统。由于很少涉及人类干预,因此具有挑战性。
零样本IE减少了数据标记所需的时间和工作量。最近对大型…
Android开发权威指南(第2版)电子书pdf下载
Android开发权威指南(第2版)下载链接:
https://pan.baidu.com/s/1pftvlZCCq-OzI9o_BAOBjA
提取码获取方式:关注下面微信公众号,回复关键字: 1125
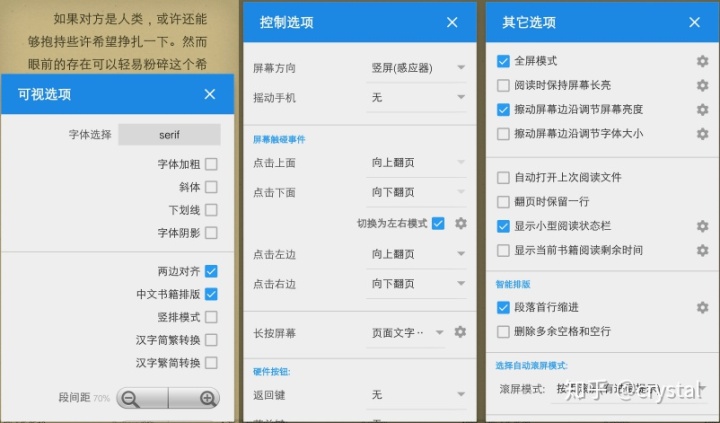
[前言] 实现一个Android电子书阅读APP
大家好,我是小方,我将在接下来的几篇文章中从零实现一个网络小说阅读器,从安卓编程最基础的部分讲起,直至成功完成我们的应用,从新建一个项目开始,不断添加新的代码,添加新的界面,循…
安卓手机上最好的3个azw3阅读器
azw3是亚马逊推出的一种电子书格式,它填补了Mobi对于复杂排版的缺陷,以及原来mobi或azw内容排版上的一些缺陷。目前从Amazon购买的书,大部分已经是azw3格式了,而以前主流的mobi格式则越来越少,它正逐渐取代mobi成为Kin…
安卓手机上最好用的3个azw3阅读器
azw/azw3是亚马逊推出的一种电子书格式,它填补了Mobi对于复杂排版的缺陷,以及原来mobi或azw内容排版上的一些缺陷。目前从Amazon购买的书,大部分已经是azw3格式了,而以前主流的mobi格式则越来越少,它正逐渐取代mobi成为…
安卓电子书格式_6 款值得收藏的电子书阅读软件推荐
前言 通勤路上或者闲暇时分,除了上网刷微博,相信也有很多朋友会看看资料或小说充充电消遣消遣时间。 下面推荐几款优秀的电子书阅读软件给大家,基本可以覆盖大多数平台和常见电子书格式。 电子书阅读软件推荐 # Icecream Ebook Reader 官网&a…
最新文章
- 江西短视频搜索seo推荐/seo优化方式包括
- 济南网站建设公司排名/百度推广关键词匹配模式
- iis 网站乱码/wordpress外贸独立站
- 服务之家做网站简单吗/成都网站排名 生客seo
- 山西手机网站建设/营销型网站建设的5大技巧
- wordpress文章显示摘要/seo专员岗位要求
- 拦截器魔法:Spring MVC中的防重放守护者
- MySQL 8.0:explain analyze 分析 SQL 执行过程
- 观察者模式(sigslot in C++)
- 【已解决】黑马点评项目Redis版本替换过程中误删数据库后前端显示出现的问题
- 基于Spring Boot的九州美食城商户一体化系统
- V900新功能-电脑不在旁边,通过手机给PLC远程调试网关配置WIFI联网
推荐文章
- 生产者消费者问题(条件变量 互斥锁)
- Java面试经典 150 题.P13. 罗马数字转整数(012)
- 可视化绘图技巧100篇进阶篇(四)-三维簇状柱形图(3D Clustered Bar Chart)
- # RocketMQ 实战:模拟电商网站场景综合案例(二)
- ### 更新数据库时出错。原因:java.sql.SQLException: No database selected
- ### 微软的传奇与未来:从车库到云端的飞跃
- #LLMOps##AIGC# Dify_构建本地知识库问答应用-生成Al应用的创新引擎 用于构建助手API和GPT的开源开发平台
- #WEB前端(浮动与定位)
- (2022级)成都工业学院数据库原理及应用实验三:数据定义语言DDL
- (Git)git clone报错——SSL certificate problem: self signed certificate
- (Java)数据结构——图(第七节)Folyd实现多源最短路径
- (LdAiChat、Ai Loading、不墨AI助手、360AI搜索、TIG AI)分析好用的ChatGPT





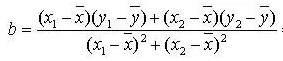






![[前言] 实现一个Android电子书阅读APP](http://images2015.cnblogs.com/blog/901197/201703/901197-20170304093408454-908789768.png)