演示求解中学数学题(Mathematica)

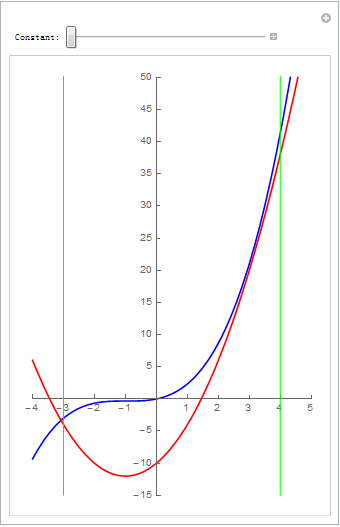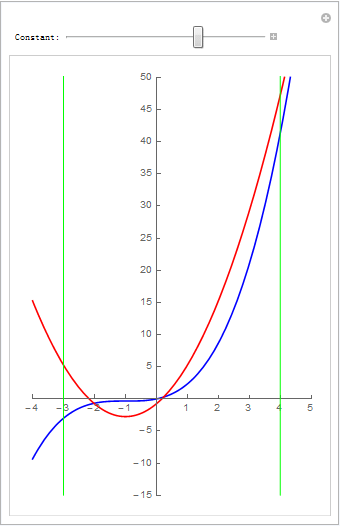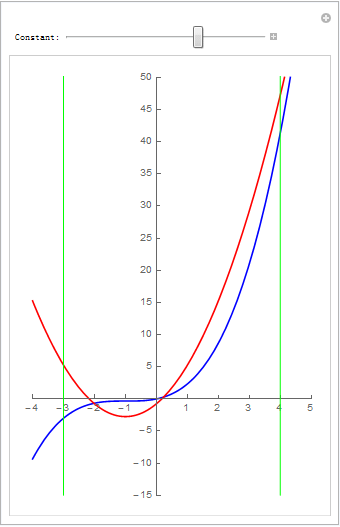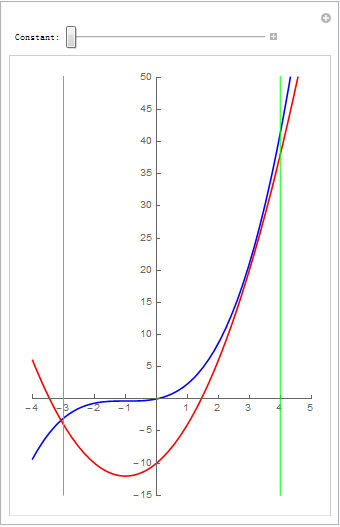
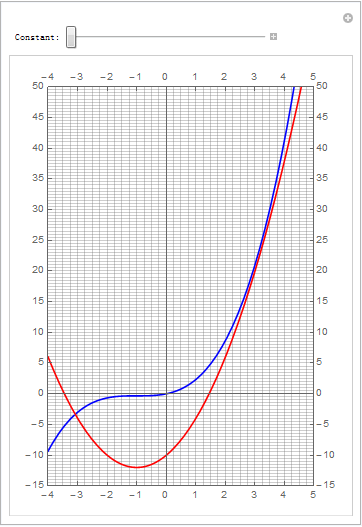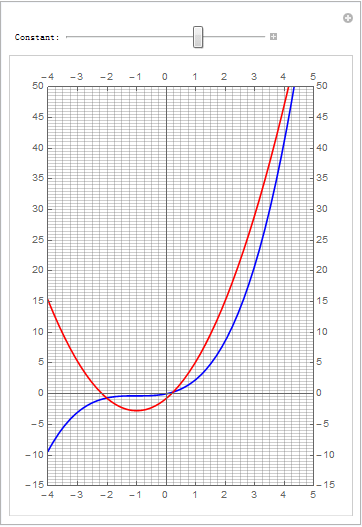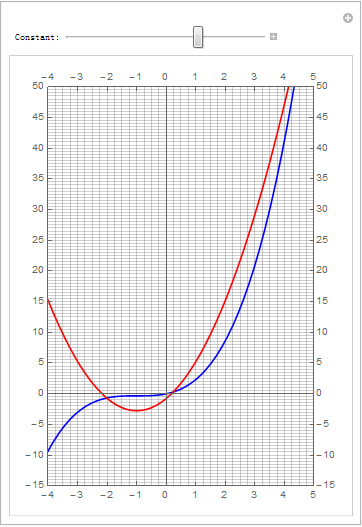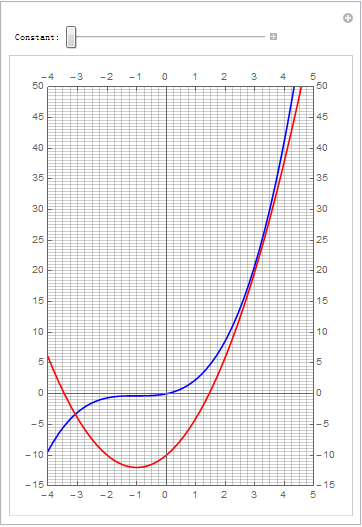
#高二解析几何题# 在[-3,4]区间上动曲线2x^2+4x+c跟曲线1/3x^3+x^2+x有两个公共点,求c的取值范围. (现在高中的数学题难度已经算是高了;需要高等数学知识了)

直接求解:

ClearAll["Global`*"]; xmin = -4; xmax = 5; ymin = -15; ymax = 50; \
xnum = 4; ynum = 2; v = Table[Manipulate[Plot[{1/3 x^3 + x^2 + x, 2 x^2 + 4 x + c}, {x, xmin, xmax}, PlotStyle -> {Blue, Red}, PlotRange -> {{xmin, xmax}, {ymin, ymax}}, Ticks -> {Table[k, {k, xmin, xmax}], Table[k*5, {k, ymin/5, ymax/5}]}, GridLines -> {Table[k/xnum, {k, xmin*xnum, xmax*xnum}], Table[k/ynum, {k, ymin*ynum, ymax*ynum}]}, AspectRatio -> 1.5, Frame -> True, FrameTicks -> {Table[k, {k, xmin, xmax}], Table[k*5, {k, ymin/5, ymax/5}]}, Axes -> True, AxesOrigin -> {0, 0}], {{c, k/4, "Constant:"}, -10, 15/4}], {k, -40, 15}]; v = Join[v[[1 ;; Dimensions[v][[1]] - 1]], Reverse[v]]; Export["testManip003.gif", v, "DisplayDurations" -> 0.1]

把 2x^2+4x+c = 1/3x^3+x^2+x 变成

c =（1/3x^3+x^2+x）-（2x^2+4x）

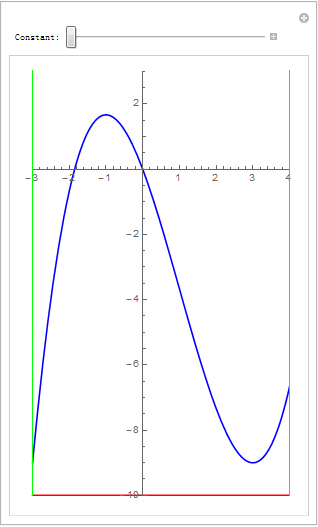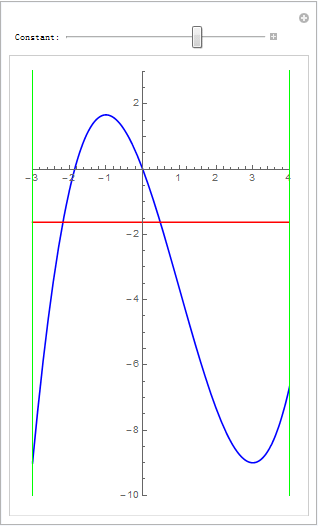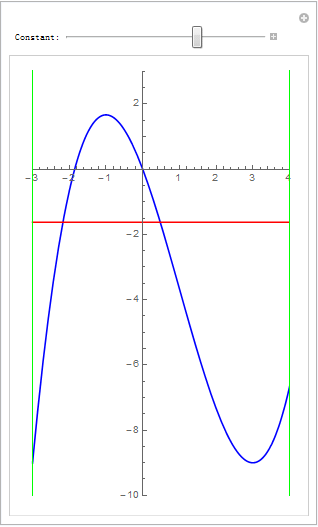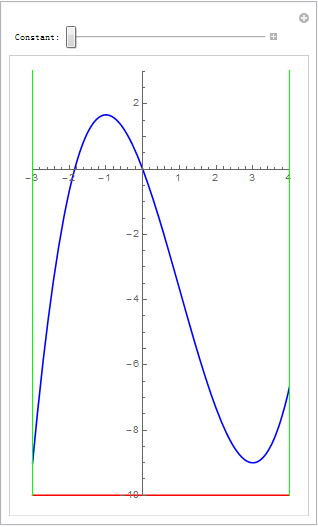
从而简化成一条三次曲线在[-3,4]区间上跟水平线y=c的交点问题则更简单:

line1 = Line[{{-3, -20}, {-3, 20}}];
line2 = Line[{{4, -20}, {4, 20}}]; slides = 8; cmin = -10; cmax = 5/2; v = Table[Manipulate[Plot[{f[x], c}, {x, -3, 4}, PlotStyle -> {Blue, Red}, AspectRatio -> 1.65, PlotRange -> {{-3, 4}, {-10, 3}}, Epilog -> {Directive[{Green, Green}], line1, line2}], {{c, k/slides, "Constant:"}, cmin, cmax}], {k, cmin*slides, cmax*slides}]; v = Join[v[[1 ;; Dimensions[v][[1]] - 1]], Reverse[v]]; Export["testManip007.gif", v, "DisplayDurations" -> 0.1]