一、数据结构的存储方式

数据结构的存储方式只有两种：数组（顺序存储）和链表（链式存储）。

二、数据结构的基本操作

对于任何数据结构，其基本操作：增删查改。
各种数据结构的遍历 + 访问无非两种形式：线性的和非线性的。
线性就是 for/while 迭代为代表，非线性就是递归为代表

• 数组遍历框架，典型的线性迭代结构：

void traverse(vector<int>& arr) {for (int i = 0; i < arr.size(); i++) {// 迭代访问 arr[i]}
}

• 链表遍历框架，兼具迭代和递归结构：

/* 基本的单链表节点 */
class ListNode {public:int val;ListNode* next;
};void traverse(ListNode* head) {for (ListNode* p = head; p != nullptr; p = p->next) {// 迭代访问 p->val}
}void traverse(ListNode* head) {// 递归访问 head->valtraverse(head->next);
}

• 二叉树遍历框架，典型的非线性递归遍历结构

/* 基本的二叉树节点 */
struct TreeNode {int val;TreeNode* left;TreeNode* right;
};void traverse(TreeNode* root) {traverse(root->left);traverse(root->right);
}

• 二叉树框架可以扩展为 N 叉树的遍历框架：

/* 基本的 N 叉树节点 */
class TreeNode {
public:int val;vector<TreeNode*> children;
};void traverse(TreeNode* root) {for (TreeNode* child : root->children)traverse(child);
}

数据结构的基本存储方式就是链式和顺序两种，基本操作就是增删查改，遍历方式无非迭代和递归。

三、双指针

3.1 数组/单链表系列算法

单链表常考的技巧就是双指针

• 首先说二分搜索技巧，可以归为两端向中心的双指针。如果让你在数组中搜索元素，一个 for 循环穷举肯定能搞定对吧，但如果数组是有序的，二分搜索不就是一种更聪明的搜索方式么。
• 滑动窗口算法技巧，典型的快慢双指针，快慢指针中间就是滑动的「窗口」，主要用于解决子串问题。教你聪明的穷举技巧。
• 还有回文串相关技巧，如果判断一个串是否是回文串，使用双指针从两端向中心检查，如果寻找回文子串，就从中心向两端扩散。
• 最后说说 前缀和技巧 和 差分数组技巧。如果频繁地让你计算子数组的和，每次用 for 循环去遍历肯定没问题，但前缀和技巧预计算一个 preSum 数组，就可以避免循环。类似的，如果频繁地让你对子数组进行增减操作，也可以每次用 for 循环去操作，但差分数组技巧维护一个 diff 数组，也可以避免循环。

3.2 滑动窗口

解决子串问题

/* 滑动窗口算法框架 */
void slidingWindow(string s) {unordered_map<char, int> window;int left = 0, right = 0;while (right < s.size()) {// c 是将移入窗口的字符char c = s[right];// 增大窗口right++;// 进行窗口内数据的一系列更新.../*** debug 输出的位置 ***/// 注意在最终的解法代码中不要 print// 因为 IO 操作很耗时，可能导致超时printf("window: [%d, %d)\n", left, right);/********************/// 判断左侧窗口是否要收缩while (window needs shrink) {// d 是将移出窗口的字符char d = s[left];// 缩小窗口left++;// 进行窗口内数据的一系列更新...}}
}

滑动窗口算法的思路是这样：

• 1、我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引左闭右开区间 [left, right) 称为一个「窗口」。
• 2、我们先不断地增加 right 指针扩大窗口 [left, right)，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。
• 3、此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right)，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。
• 4、重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

在我们来看看这个滑动窗口代码框架怎么用：

• 首先，初始化 window 和 need 两个哈希表，记录窗口中的字符和需要凑齐的字符：

unordered_map<char, int> need, window;
for (char c : t) need[c]++;

• 然后，使用 left 和 right 变量初始化窗口的两端，不要忘了，区间 [left, right) 是左闭右开的，所以初始情况下窗口没有包含任何元素：

int left = 0, right = 0;
int valid = 0; 
while (right < s.size()) {// 开始滑动
}

其中 valid 变量表示窗口中满足 need 条件的字符个数，如果 valid 和 need.size 的大小相同，则说明窗口已满足条件，已经完全覆盖了串 T。
现在开始套模板，只需要思考以下几个问题：

• 1、什么时候应该移动 right 扩大窗口？窗口加入字符时，应该更新哪些数据？

• 2、什么时候窗口应该暂停扩大，开始移动 left 缩小窗口？从窗口移出字符时，应该更新哪些数据？

• 3、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

回答：如果一个字符进入窗口，应该增加 window 计数器；如果一个字符将移出窗口的时候，应该减少 window 计数器；当 valid 满足 need 时应该收缩窗口；应该在收缩窗口的时候更新最终结果。

3.3 二分查找

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。
另外提前说明一下，计算 mid 时需要防止溢出，代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同，但是有效防止了 left 和 right 太大，直接相加导致溢出的情况。

3.3.1 寻找一个数（基本的二分搜索）

int binarySearch(vector<int>& nums, int target) {int left = 0; int right = nums.size() - 1; // 注意while(left <= right) {int mid = left + (right - left) / 2;if(nums[mid] == target)return mid; else if (nums[mid] < target)left = mid + 1; // 注意else if (nums[mid] > target)right = mid - 1; // 注意}return -1;
}

• 1、为什么 while 循环的条件中是 <=，而不是 <？

答：区别是：前者的搜索区间为 [left, right]，后者相当 [left, right)。搜索区间为空的时候应该终止。
while(left <= right) 的终止条件是 left == right + 1，写成区间的形式就是 [right + 1, right]，可见这时候区间为空，所以这时候 while 循环终止是正确的，直接返回 -1 即可。
while(left < right) 的终止条件是 left == right，写成区间的形式就是 [right, right]，这时候区间非空，区间 [right, right]被漏掉了，索引 right 没有被搜索，如果这时候直接返回 -1 就是错误的。

• 2、为什么 left = mid + 1，right = mid - 1？我看有的代码是 right = mid 或者 left = mid，没有这些加加减减，到底怎么回事，怎么判断？

答：发现索引 mid 不是要找的 target 时，下一步应该去搜索区间 [left, mid-1] 或者区间 [mid+1, right] 。因为 mid 已经搜索过，应该从搜索区间中去除。

• 3、此算法有什么缺陷？
  答：想得到 target 的左侧边界，或右侧边界，算法是无法处理的。而找到一个 target，然后向左或向右线性搜索会破坏二分查找对数级的复杂度。

3.3.2 寻找左侧边界的二分搜索(搜索区间向左靠拢)

int left_bound(vector<int>& nums, int target) {int left = 0;int right = nums.size(); // 注意while (left < right) { // 注意int mid = left + (right - left) / 2;if (nums[mid] == target) {right = mid;} else if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid; // 注意}}return left;
}

• 1、为什么 while 中是 < 而不是 <=?

答：用相同的方法分析，因为 right = nums.length 而不是 nums.length - 1。因此每次循环的「搜索区间」是 [left, right) 左闭右开。

while(left < right) 终止的条件是 left == right，此时搜索区间 [left, left) 为空，所以可以正确终止。

• 2、为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？

答：其实很简单，在返回的时候额外判断一下 nums[left] 是否等于 target 就行了，如果不等于，就说明 target 不存在。不过我们得考察一下 left 的取值范围，免得索引越界。由于这里 right 初始化为 nums.length，所以 left 变量的取值区间是闭区间 [0, nums.length]，那么我们在检查 nums[left] 之前需要额外判断一下，防止索引越界：

while (left < right) {//...
}
// 此时 target 比所有数都大，返回 -1
if (left == nums.length) return -1;
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;

• 3、为什么 left = mid + 1，right = mid ？和之前的算法不一样？

答：这个很好解释，因为我们的「搜索区间」是 [left, right) 左闭右开，所以当 nums[mid] 被检测之后，下一步应该去 mid 的左侧或者右侧区间搜索，即 [left, mid) 或 [mid + 1, right)。

• 4、为什么该算法能够搜索左侧边界？

答：关键在于对于 nums[mid] == target 这种情况的处理：

   if (nums[mid] == target)right = mid;

可见，找到 target 时不要立即返回，而是缩小「搜索区间」的上界 right，在区间 [left, mid) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。

• 5、为什么返回 left 而不是 right？

答：都是一样的，因为 while 终止的条件是 left == right。

• 6、能不能想办法把 right 变成 nums.length - 1，也就是继续使用两边都闭的「搜索区间」？这样就可以和第一种二分搜索在某种程度上统一起来了。

答：当然可以，只要你明白了「搜索区间」这个概念，就能有效避免漏掉元素，随便你怎么改都行。下面我们严格根据逻辑来修改：

int left_bound(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;// 搜索区间为 [left, right]while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {// 搜索区间变为 [mid+1, right]left = mid + 1;} else if (nums[mid] > target) {// 搜索区间变为 [left, mid-1]right = mid - 1;} else if (nums[mid] == target) {// 收缩右侧边界right = mid - 1;}}// 判断 target 是否存在于 nums 中// 此时 target 比所有数都大，返回 -1if (left == nums.size()) return -1;// 判断一下 nums[left] 是不是 targetreturn nums[left] == target ? left : -1;
}

3.3.3 寻找右侧边界的二分查找（搜索区间向右靠拢）

int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size();while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {left = mid + 1; // 注意} else if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid;}}return left - 1; // 注意
}

• 1、为什么这个算法能够找到右侧边界？

if (nums[mid] == target) {left = mid + 1;

当 nums[mid] == target 时，不要立即返回，而是增大「搜索区间」的左边界 left，使得区间不断向右靠拢，达到锁定右侧边界的目的。

• 2、为什么最后返回 left - 1 而不像左侧边界的函数，返回 left？而且我觉得这里既然是搜索右侧边界，应该返回 right 才对。

// 增大 left，锁定右侧边界
if (nums[mid] == target) {left = mid + 1;// 这样想: mid = left - 1

答：首先，while 循环的终止条件是 left == right，所以 left 和 right 是一样的，你非要体现右侧的特点，返回 right - 1 好了。
什么 left 的更新必须是 left = mid + 1，当然是为了把 nums[mid] 排除出搜索区间

• 3、为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？
  答：只要在最后判断一下 nums[left-1] 是不是 target 就行了。
  类似之前的左侧边界搜索，left 的取值范围是 [0, nums.length]，但由于我们最后返回的是 left - 1，所以 left 取值为 0 的时候会造成索引越界，额外处理一下即可正确地返回 -1：

while (left < right) {// ...
}
// 判断 target 是否存在于 nums 中
// 此时 left - 1 索引越界
if (left - 1 < 0) return -1;
// 判断一下 nums[left] 是不是 target
return nums[left - 1] == target ? (left - 1) : -1;

• 4、是否也可以把这个算法的「搜索区间」也统一成两端都闭的形式呢？这样这三个写法就完全统一了，以后就可以闭着眼睛写出来了。
  答：当然可以，类似搜索左侧边界的统一写法，其实只要改两个地方就行了：

int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 这里改成收缩左侧边界即可left = mid + 1;}}// 最后改成返回 left - 1if (left - 1 < 0) return -1;return nums[left - 1] == target ? (left - 1) : -1;
}

统一一下可以总结为：

int binary_search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1; while(left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1; } else if(nums[mid] == target) {// 直接返回return mid;}}// 直接返回return -1;
}int left_bound(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 别返回，锁定左侧边界right = mid - 1;}}// 判断 target 是否存在于 nums 中// 此时 target 比所有数都大，返回 -1if (left == nums.size()) return -1;// 判断一下 nums[left] 是不是 targetreturn nums[left] == target ? left : -1;
}int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 别返回，锁定右侧边界left = mid + 1;}}// 此时 left - 1 索引越界if (right < 0) return -1;// 判断一下 nums[left] 是不是 targetreturn nums[right] == target ? (left - 1) : -1;
}

二分查找某个值，左边界，右边界的区别主要是两个地方不同：

1. 当 nums[mid] == target时

• 寻找某个值

return mid;

• 寻找左边界时，搜索区间向左靠拢

right = mid - 1;

• 寻找右边界，搜索区间向右靠拢

left = mid + 1;

2. 当结束循环时

• 寻找某个值

return -1；

• 寻找左边界

if(left > nums.size()) return -1;
return nums[left] == target? left : -1;

• 寻找右边界

if(right < 0) return -1;
return nums[right] == target? right : -1;

3.3.4 二分查找的泛化

因为算法题一般都让你求最值，比如让你求吃香蕉的「最小速度」，让你求轮船的「最低运载能力」，求最值的过程，必然是搜索一个边界的过程。

1. 首先，要从题目中抽象出

• 一个自变量 x
• 一个关于 x 的函数 f(x)
• 一个目标值
  同时，满足以下条件：
• f(x) 是在 x 上的单调函数
• 题目要求是让计算满足约束条件 f(x) == targer 时 x 的值
  如图所示：
  
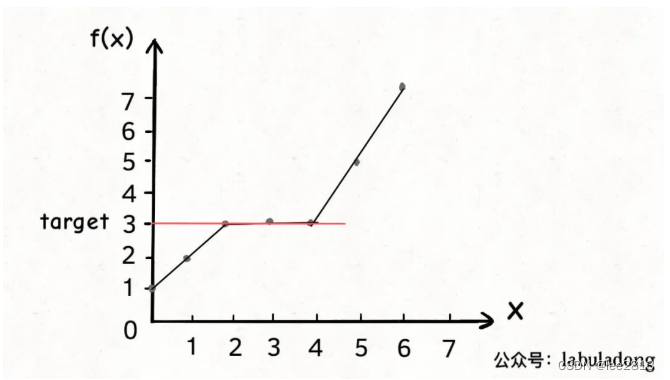
  对应的代码如下：
  

3.3.5 二分搜索的框架

确定可以用双指针且对应的算法流程分为三步：

2. 确认x , f(x), target分别是什么，并写出函数 f 的代码
3. 找到 x 的取值范围作为二分搜索的区间，初始化 left 和 right 变量
4. 根据题目要求，确定使用左边界搜索还是右边界搜索，并写出解法代码

3.4 两数之和

一、twoSum 问题

• 先对 nums 排序,基本思路还是排序加双指针：

vector<vector<int>> twoSumTarget(vector<int>& nums, int target {// 先对数组排序sort(nums.begin(), nums.end());vector<vector<int>> res;int lo = 0, hi = nums.size() - 1;while (lo < hi) {int sum = nums[lo] + nums[hi];// 根据 sum 和 target 的比较，移动左右指针if      (sum < target) lo++;else if (sum > target) hi--;else {res.push_back({lo, hi});lo++; hi--;}}return res;
}

• sum == target 条件的 if 分支，当给 res 加入一次结果后，lo 和 hi 不应该改变 1 的同时，还应该跳过所有重复的元素，可修改如下：

vector<vector<int>> twoSumTarget(vector<int>& nums, int target) {// nums 数组必须有序sort(nums.begin(), nums.end());int lo = 0, hi = nums.size() - 1;vector<vector<int>> res;while (lo < hi) {int sum = nums[lo] + nums[hi];int left = nums[lo], right = nums[hi];if (sum < target) {while (lo < hi && nums[lo] == left) lo++;} else if (sum > target) {while (lo < hi && nums[hi] == right) hi--;} else {res.push_back({left, right});while (lo < hi && nums[lo] == left) lo++;while (lo < hi && nums[hi] == right) hi--;}}return res;
}

3.5 nSum 问题

3.5.1 2sum

• 于第一个数字，nums[i] 都有可能。确定了第一个数字之后，剩下的两个数字就是和为 target - nums[i] 的两个数字，也就是 twoSum问题。

/* 从 nums[start] 开始，计算有序数组* nums 中所有和为 target 的二元组 */
vector<vector<int>> twoSumTarget(vector<int>& nums, int start, int target) {// 左指针改为从 start 开始，其他不变int lo = start, hi = nums.size() - 1;vector<vector<int>> res;while (lo < hi) {int sum = nums[lo] + nums[hi];int left = nums[lo], right = nums[hi];if (sum < target) {while (lo < hi && nums[lo] == left) lo++;} else if (sum > target) {while (lo < hi && nums[hi] == right) hi--;} else {res.push_back({left, right});while (lo < hi && nums[lo] == left) lo++;while (lo < hi && nums[hi] == right) hi--;}}return res;
}/* 计算数组 nums 中所有和为 target 的三元组 */
vector<vector<int>> threeSumTarget(vector<int>& nums, int target) {// 数组得排个序sort(nums.begin(), nums.end());int n = nums.size();vector<vector<int>> res;// 穷举 threeSum 的第一个数for (int i = 0; i < n; i++) {// 对 target - nums[i] 计算 twoSumvector<vector<int>> tuples = twoSumTarget(nums, i + 1, target - nums[i]);// 如果存在满足条件的二元组，再加上 nums[i] 就是结果三元组for (vector<int>& tuple : tuples) {tuple.push_back(nums[i]);res.push_back(tuple);}// 跳过第一个数字重复的情况，否则会出现重复结果while (i < n - 1 && nums[i] == nums[i + 1]) i++;}return res;
}

需要注意的是，类似 twoSum，3Sum 的结果也可能重复。关键点在于，不能让第一个数重复，至于后面的两个数，我们复用的 twoSum 函数会保证它们不重复。所以代码中必须用一个 while 循环来保证 3Sum 中第一个元素不重复。

3.5.2 Sum和问题

vector<vector<int>> fourSum(vector<int>& nums, int target) {// 数组需要排序sort(nums.begin(), nums.end());int n = nums.size();vector<vector<int>> res;// 穷举 fourSum 的第一个数for (int i = 0; i < n; i++) {// 对 target - nums[i] 计算 threeSumvector<vector<int>> triples = threeSumTarget(nums, i + 1, target - nums[i]);// 如果存在满足条件的三元组，再加上 nums[i] 就是结果四元组for (vector<int>& triple : triples) {triple.push_back(nums[i]);res.push_back(triple);}// fourSum 的第一个数不能重复while (i < n - 1 && nums[i] == nums[i + 1]) i++;}return res;
}/* 从 nums[start] 开始，计算有序数组* nums 中所有和为 target 的三元组 */
vector<vector<int>> threeSumTarget(vector<int>& nums, int start, int target) {int n = nums.size();vector<vector<int>> res;// i 从 start 开始穷举，其他都不变for (int i = start; i < n; i++) {// 对 target - nums[i] 计算 twoSumvector<vector<int>> tuples = twoSumTarget(nums, i + 1, target - nums[i]);// 如果存在满足条件的二元组，再加上 nums[i] 就是结果三元组for (vector<int>& tuple : tuples) {tuple.push_back(nums[i]);res.push_back(tuple);}// 跳过第一个数字重复的情况，否则会出现重复结果while (i < n - 1 && nums[i] == nums[i + 1]) i++;}return res;

3.5.3 100Sum问题

可统一的函数为：

/* 注意：调用这个函数之前一定要先给 nums 排序 */
vector<vector<int>> nSumTarget(vector<int>& nums, int n, int start, int target) {vector<vector<int>> res;// 至少是 2Sum，且数组大小不应该小于 nif (n < 2 || nums.size() < n) return res;// 2Sum 是 base caseif (n == 2) {// 双指针那一套操作int lo = start, hi = nums.size() - 1;while (lo < hi) {int sum = nums[lo] + nums[hi];int left = nums[lo], right = nums[hi];if (sum < target) {while (lo < hi && nums[lo] == left) lo++;} else if (sum > target) {while (lo < hi && nums[hi] == right) hi--;} else {res.push_back({left, right});while (lo < hi && nums[lo] == left) lo++;while (lo < hi && nums[hi] == right) hi--;}}} else if(n > 2){// n > 2 时，递归计算 (n-1)Sum 的结果for (int i = start; i < nums.size(); i++) {vector<vector<int>> sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);for (vector<int>& arr : sub) {// (n-1)Sum 加上 nums[i] 就是 nSumarr.push_back(nums[i]);res.push_back(arr);}while (i < nums.size() - 1 && nums[i] == nums[i + 1]) i++;}}return res;
}

如果在 nSum 函数里调用排序函数，那么每次递归都会进行没有必要的排序，效率会非常低。因此，在调用函数之前，应该先给 nums 进行排序。例如：

vector<vector<int>> fourSum(vector<int>& nums, int target) {sort(nums.begin(), nums.end());// n 为 4，从 nums[0] 开始计算和为 target 的四元组return nSumTarget(nums, 4, 0, target);
}

四、二叉树系列算法

对递归的理解不到位，更应该好好刷二叉树相关题目。
二叉树题目的递归解法可以分两类思路：

• 第一类是遍历一遍二叉树得出答案？—— 回溯算法核心框架
  如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。

• 第二类是通过分解问题计算出答案？—— 动态规划核心框架。
  即是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

• PS:无论使用哪种思维模式，你都需要思考：
  如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？其他的节点不用操心，递归函数会帮你在所有节点上执行相同的操作。

4.1 深入理解前中后序（递归之前——前序位置；递归之后——后序位置）

void traverse(TreeNode* root) {if (root == nullptr) {return;}// 前序位置traverse(root->left);// 中序位置traverse(root->right);// 后序位置
}//递归遍历单链表
void traverse(ListNode* head) {if (head == nullptr) {return;}//前序位置traverse(head -> next);//后序位置
}

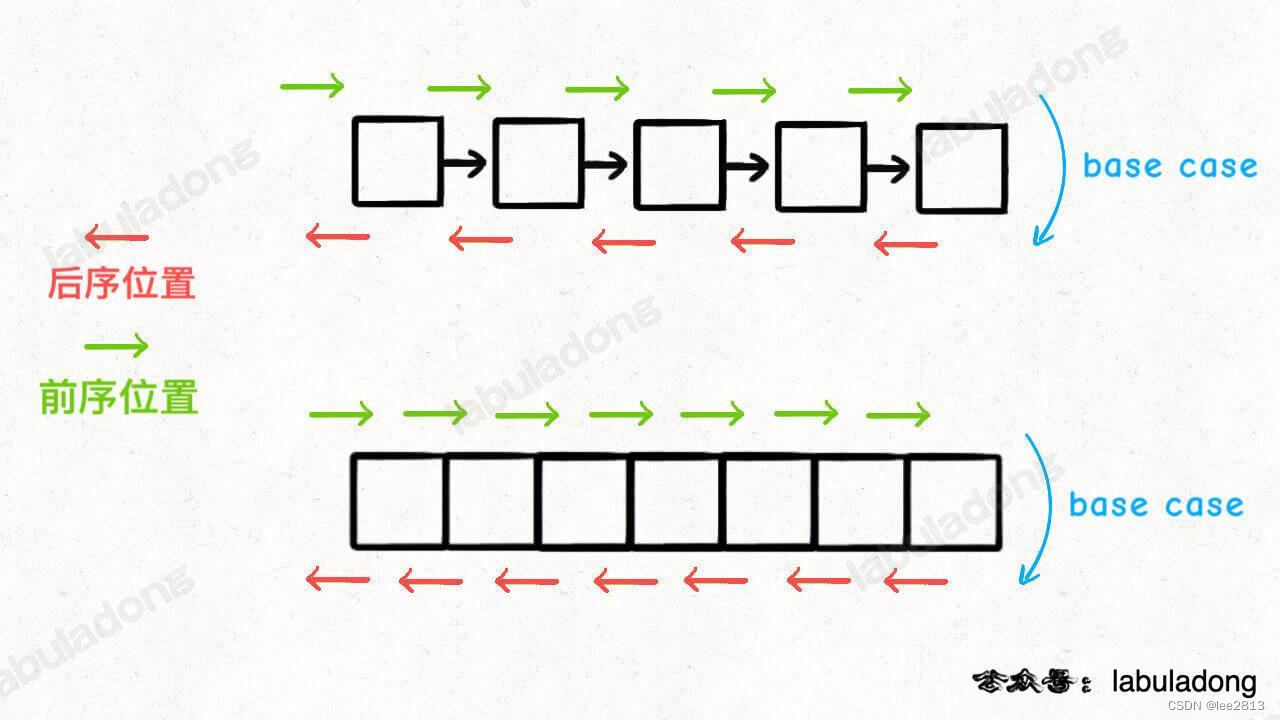
• 单链表和数组的遍历可以是迭代的（从前往后单向传递），也可以是递归的（从前往后传递，再从后往前传递），二叉树的遍历框架都是指递归的形式。
• 只要是递归形式的遍历，都可以有前序位置和后序位置，分别在递归之前和递归之后。
• 所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候
• 前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点
• 二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。

综上，遇到一道二叉树的题目时的通用思考过程是：

• 1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现。

• 2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。

• 3、无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

什么叫通过遍历一遍二叉树得出答案？ 计算二叉树最大深度

class Solution {
public:// 记录最大深度int res = 0;int depth = 0;// 主函数int maxDepth(TreeNode* root) {traverse(root);return res;}// 二叉树遍历框架void traverse(TreeNode* root) {if (root == NULL) {// 到达叶子节点return;}// 前序遍历位置depth++;if(root->left == nullptr && root->right == nullptr){res = max(res, depth);}traverse(root->left);traverse(root->right);// 后序遍历位置depth--;}
};

回溯算法的时候就告诉你回溯算法本质就是遍历一棵多叉树

class Solution {
public:// 记录所有全排列vector<vector<int>> res;vector<int> track;/* 主函数，输入一组不重复的数字，返回它们的全排列 */vector<vector<int>> permute(vector<int>& nums) {backtrack(nums);return res;}// 回溯算法框架void backtrack(vector<int>& nums) {if (track.size() == nums.size()) {// 穷举完一个全排列res.push_back(track);return;}for (int i = 0; i < nums.size(); i++) {if (find(track.begin(), track.end(), nums[i]) != track.end()) continue;// 前序遍历位置做选择track.push_back(nums[i]);backtrack(nums);// 后序遍历位置取消选择track.pop_back();}}
};

• 那什么叫通过分解问题计算答案？
  也就是利用子问题的答案来推导出父问题的答案。
  同样是计算二叉树最大深度这个问题，你也可以写出下面这样的解法：

// 定义：输入根节点，返回这棵二叉树的最大深度
int maxDepth(TreeNode* root) {if (root == nullptr) {return 0;}// 递归计算左右子树的最大深度int leftMax = maxDepth(root->left);int rightMax = maxDepth(root->right);// 整棵树的最大深度int res = max(leftMax, rightMax) + 1;return res;
}

同样的，前序遍历也可以从两种思路来进行求解：

• 遍历二叉树的思路：

#include <iostream>
#include <vector>using namespace std;vector<int> res;// 前序遍历结果
vector<int> preorderTraverse(TreeNode* root) {traverse(root);return res;
}// 二叉树遍历函数
void traverse(TreeNode* root) {if (root == nullptr) {return;}// 前序位置res.push_back(root->val);traverse(root->left);traverse(root->right);
}

• 分解子问题的思路：

// 定义：输入一棵二叉树的根节点，返回这棵树的前序遍历结果
vector<int> preorderTraverse(TreeNode* root) {vector<int> res;if (root == nullptr) {return res;}// 前序遍历的结果，root->val 在第一个res.push_back(root->val);// 利用函数定义，后面接着左子树的前序遍历结果vector<int> leftRes = preorderTraverse(root->left);res.insert(res.end(), leftRes.begin(), leftRes.end());// 利用函数定义，最后接着右子树的前序遍历结果vector<int> rightRes = preorderTraverse(root->right);res.insert(res.end(), rightRes.begin(), rightRes.end());return res;
}

不信你看 动态规划核心框架 中凑零钱问题的暴力穷举解法：

// 定义：输入金额 amount，返回凑出 amount 的最少硬币个数
int coinChange(vector<int>& coins, int amount) {// base caseif (amount == 0) return 0;if (amount < 0) return -1;int res = INT_MAX;for (int coin : coins) {// 递归计算凑出 amount - coin 的最少硬币个数int subProblem = coinChange(coins, amount - coin);if (subProblem == -1) continue;// 凑出 amount 的最少硬币个数res = min(res, subProblem + 1);}return res == INT_MAX ? -1 : res;
}

• 分治算法详解 中说到的运算表达式优先级问题，其核心依然是大问题分解成子问题，只不过没有重叠子问题，不能用备忘录去优化效率罢了。
• 比如 图论基础， 环判断和拓扑排序 和 二分图判定算法 就用到了 DFS 算法；再比如 Dijkstra 算法模板，就是改造版 BFS 算法加上一个类似 dp table 的数组。

二叉树题目的思考思路为：

• 1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现。

• 2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。

• 3、无论使用哪一种思维模式，都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

4.2 后序位置的特殊之处：

1. 中序位置主要用在 BST 场景中，完全可以把 BST 的中序遍历认为是遍历有序数组。
2. 前序位置本身其实没有什么特别的性质，对前中后序位置不敏感的代码写在前序位置罢了。
3. 前序位置的代码执行是自顶向下的，而后序位置的代码执行是自底向上的： 意味着前序位置的代码只能从函数参数中获取父节点传递来的数据，而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。

具体的例子，现在给你一棵二叉树，我问你两个简单的问题：
1、如果把根节点看做第 1 层，如何打印出每一个节点所在的层数？

// 二叉树遍历函数
void traverse(TreeNode* root, int level) {if (root == NULL) {return;}// 前序位置printf("节点 %s 在第 %d 层", root, level);traverse(root->left, level + 1);traverse(root->right, level + 1);
}// 这样调用
traverse(root, 1);

2、如何打印出每个节点的左右子树各有多少节点？

// 定义：输入一棵二叉树，返回这棵二叉树的节点总数
int count(TreeNode* root) {if (root == nullptr) {return 0;}int leftCount = count(root->left);int rightCount = count(root->right);// 后序位置printf("节点 %s 的左子树有 %d 个节点，右子树有 %d 个节点",root->val, leftCount, rightCount);return leftCount + rightCount + 1;
}

根本区别在于：

• 一个节点在第几层，从根节点遍历过来的过程就能顺带记录；
• 而以一个节点为根的整棵子树有多少个节点，需要遍历完子树之后才能数清楚。

后序位置的特点，只有后序位置才能通过返回值获取子树的信息。
也就是说，一旦发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

五、回溯算法

回溯算法和常说的 DFS 算法非常类似，本质上就是一种暴力穷举算法。回溯算法和 DFS 算法的细微差别是：回溯算法是在遍历「树枝」，DFS 算法是在遍历「节点」。
解决一个回溯问题，实际上就是一个决策树的遍历过程，站在回溯树的一个节点上，你只需要思考 3 个问题：

• 1、路径：也就是已经做出的选择。

• 2、选择列表：也就是你当前可以做的选择。

• 3、结束条件：也就是到达决策树底层，无法再做选择的条件。

result = []
def backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择

核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」

5.1 全排列问题

只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。

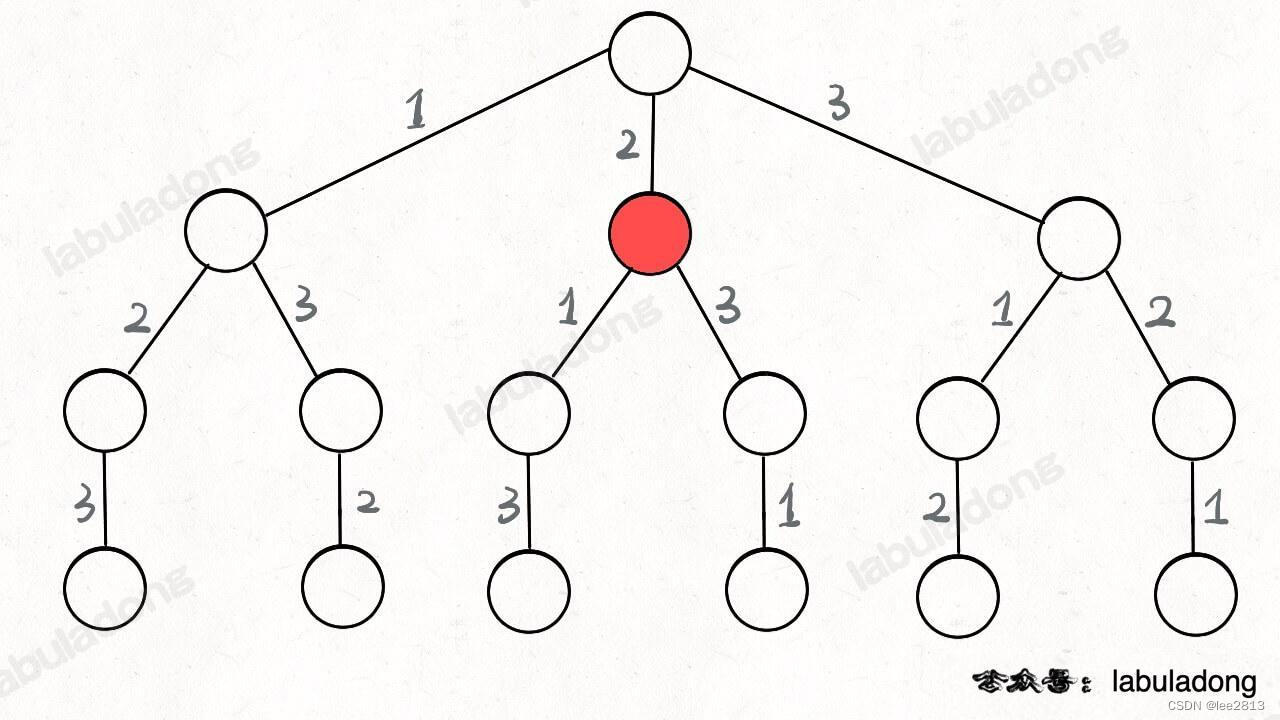
你现在就在做决策，可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢？因为 2 这个树枝在你身后，这个选择你之前做过了，而全排列是不允许重复使用数字的。
现在可以解答开头的几个名词：[2] 就是「路径」，记录你已经做过的选择；[1,3] 就是「选择列表」，表示你当前可以做出的选择；「结束条件」就是遍历到树的底层叶子节点，这里也就是选择列表为空的时候。

定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层叶子节点，其「路径」就是一个全排列。
多叉树的遍历框架就是这样：

void traverse(TreeNode* root) {for (TreeNode* child : root->childern) {// 前序位置需要的操作traverse(child);// 后序位置需要的操作}
}

而所谓的前序遍历和后序遍历，他们只是两个很有用的时间点
前序遍历的代码在进入某一个节点之前的那个时间点执行，后序遍历代码在离开某个节点之后的那个时间点执行。「路径」和「选择」是每个节点的属性，函数在树上游走要正确处理节点的属性，那么就要在这两个特殊时间点搞点动作：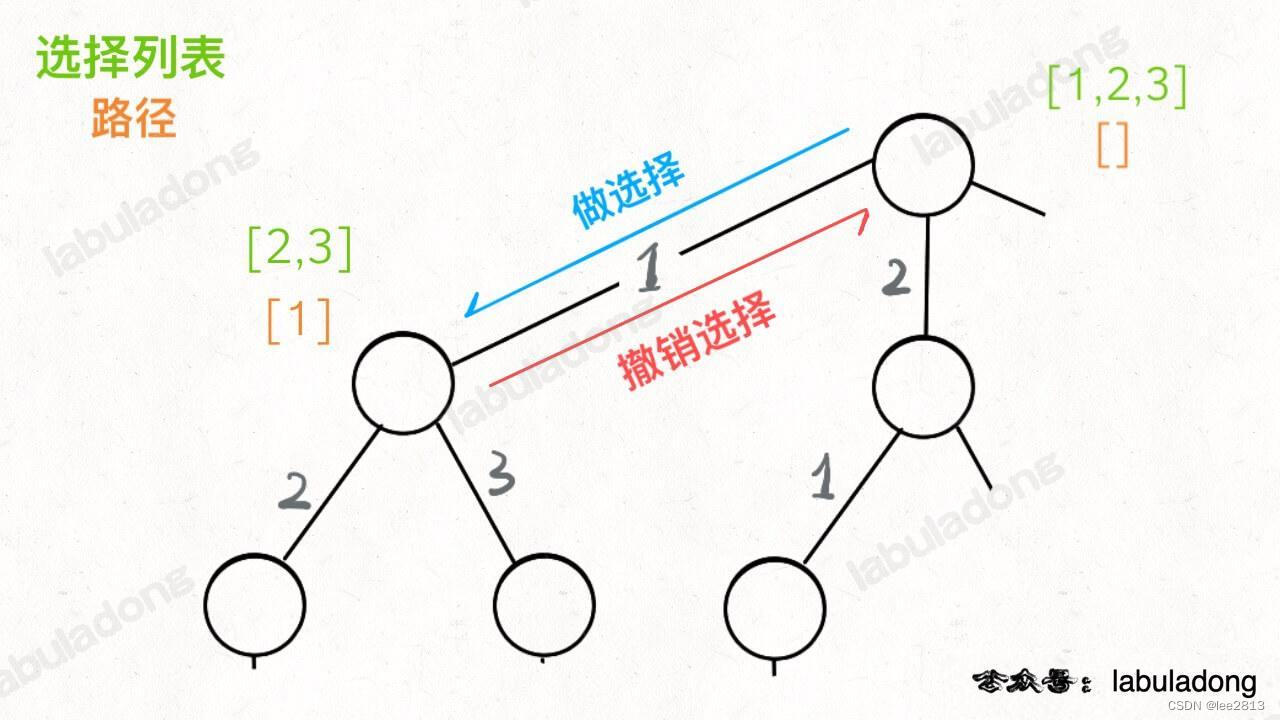

for 选择 in 选择列表:# 做选择将该选择从选择列表移除路径.add(选择)backtrack(路径, 选择列表)# 撤销选择路径.remove(选择)将该选择再加入选择列表

只要在递归之前做出选择，在递归之后撤销刚才的选择，就能正确得到每个节点的选择列表和路径。

class Solution {private:vector<vector<int>> res;/* 主函数，输入一组不重复的数字，返回它们的全排列 */vector<vector<int>> permute(vector<int>& nums) {// 记录「路径」vector<int> track;//「路径」中的元素会被标记为true，避免重复使用vector<bool> used(nums.size(), false);backtrack(nums, track, used);return res;}// 路径：记录在 track 中// 选择列表：nums 中不存在于 track 的那些元素// 结束条件：nums 中的元素全都在 track 中出现void backtrack(vector<int>& nums, vector<int>& track, vector<bool>& used) {// 触发结束条件if (track.size() == nums.size()) {res.push_back(track);return;}for (int i = 0; i < nums.size(); i++) {// 排除不合法的选择if (used[i]) {//nums[i] 已经在 track中，跳过continue;}// 做选择track.push_back(nums[i]);used[i] = true;// 进入下一层决策树backtrack(nums, track, used);// 取消选择track.pop_back();used[i] = false;}}public:vector<vector<int>> permute(vector<int>& nums) {return permute(nums);}
};

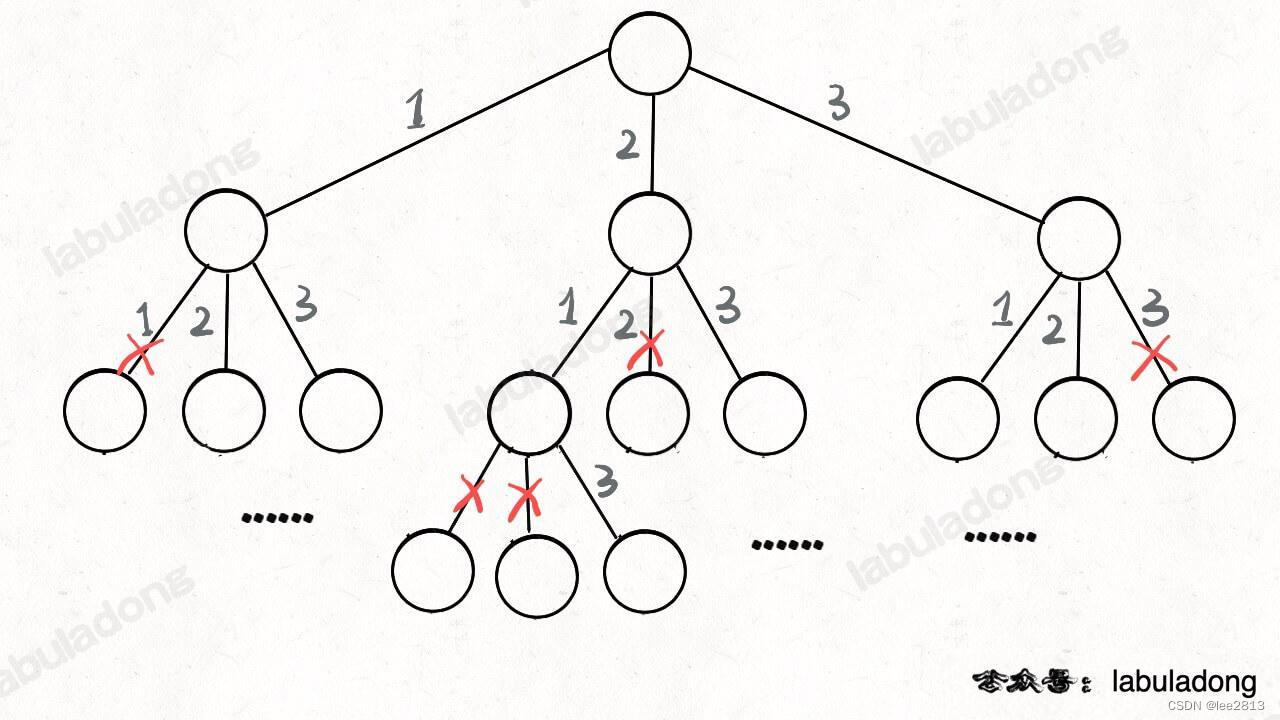
这里稍微做了些变通，没有显式记录「选择列表」，而是通过 used 数组排除已经存在 track 中的元素，从而推导出当前的选择列表：

5.2 n皇后问题

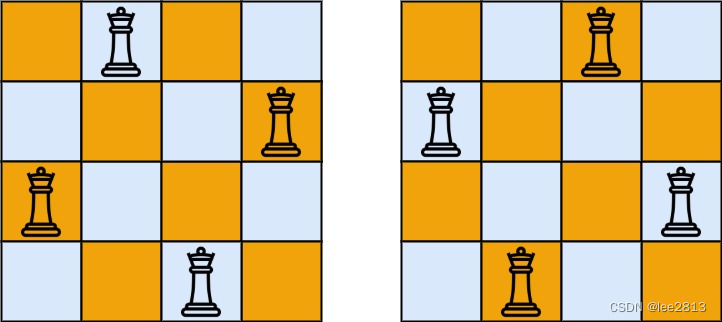
• 1.列出n皇后所有的解法

class Solution {
public:vector<vector<string>> res;/* 输入棋盘边长 n，返回所有合法的放置 */vector<vector<string>> solveNQueens(int n) {// vector<string> 代表一个棋盘// '.' 表示空，'Q' 表示皇后，初始化空棋盘vector<string> board(n, string(n, '.'));backtrack(board, 0);return res;}// 路径：board 中小于 row 的那些行都已经成功放置了皇后// 选择列表：第 row 行的所有列都是放置皇后的选择// 结束条件：row 超过 board 的最后一行void backtrack(vector<string>& board, int row) {// 触发结束条件if (row == board.size()) {res.push_back(board);return;}int n = board[row].size();for (int col = 0; col < n; col++) {// 排除不合法选择if (!isValid(board, row, col)) {continue;}// 做选择board[row][col] = 'Q';// 进入下一行决策backtrack(board, row + 1);// 撤销选择board[row][col] = '.';}}
}

• 2.列出一个解法：满足条件后直接停止递归

bool found = false;
// 函数找到一个答案后就返回 true
bool backtrack(vector<string>& board, int row) {if (found) {// 已经找到一个答案了，不用再找了return;}// 触发结束条件if (row == board.size()) {res.push_back(board);// 找到了第一个答案found = true;return;}...
}

• 3.存储有多少个解

// 仅仅记录合法结果的数量
int res = 0;void backtrack(vector<string>& board, int row) {if (row == board.size()) {// 找到一个合法结果res++;return;}// 其他都一样
}

5.3 排列-组合-子树问题

无论形式怎么变化，其本质就是穷举所有解，而这些解呈现树形结构，所以合理使用回溯算法框架，稍改代码框架即可。


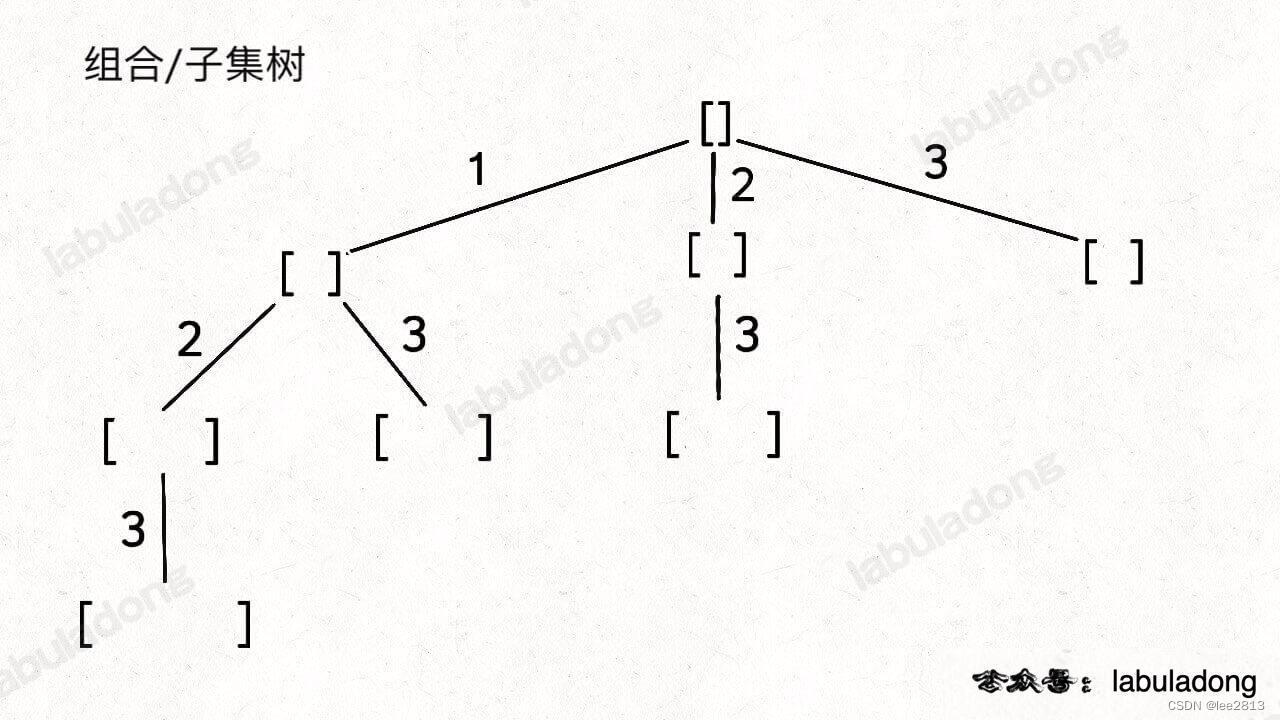
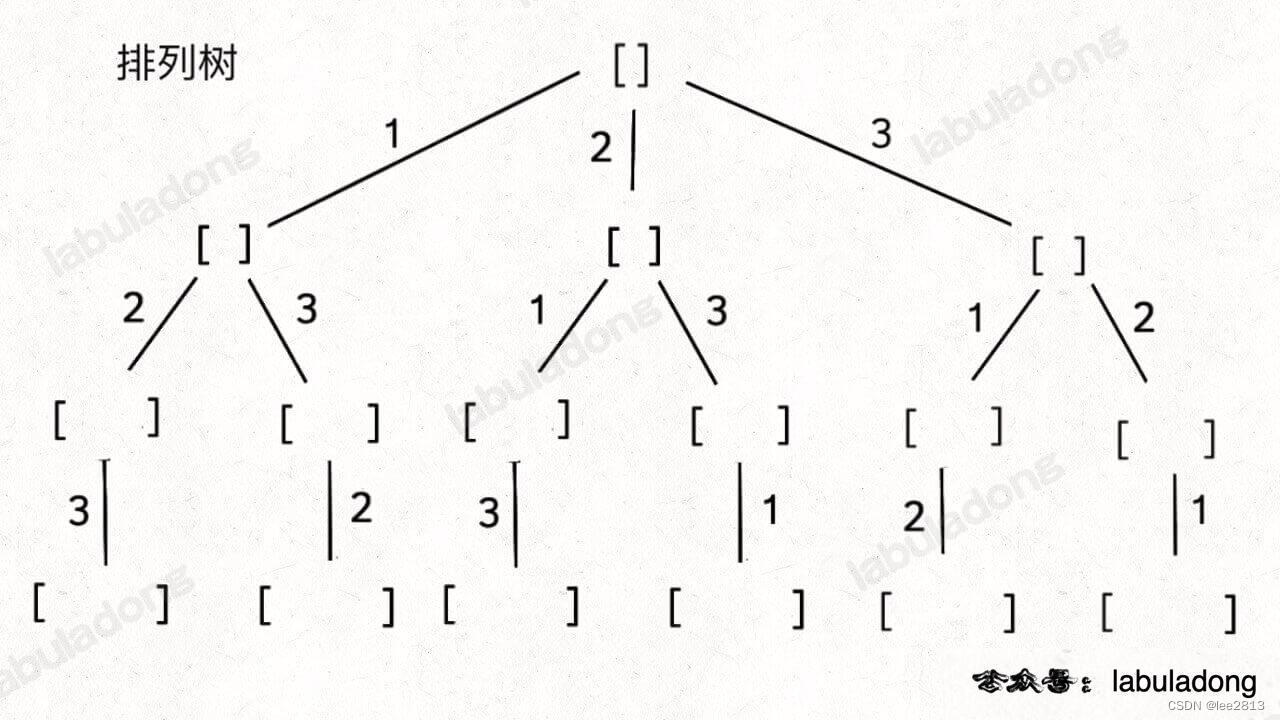
首先，组合问题和子集问题是等价的，问题的变化形式，就是在这两棵树上剪掉或者增加一些树枝。

5.4 子集（元素无重不可复选）—— 返回递归路径

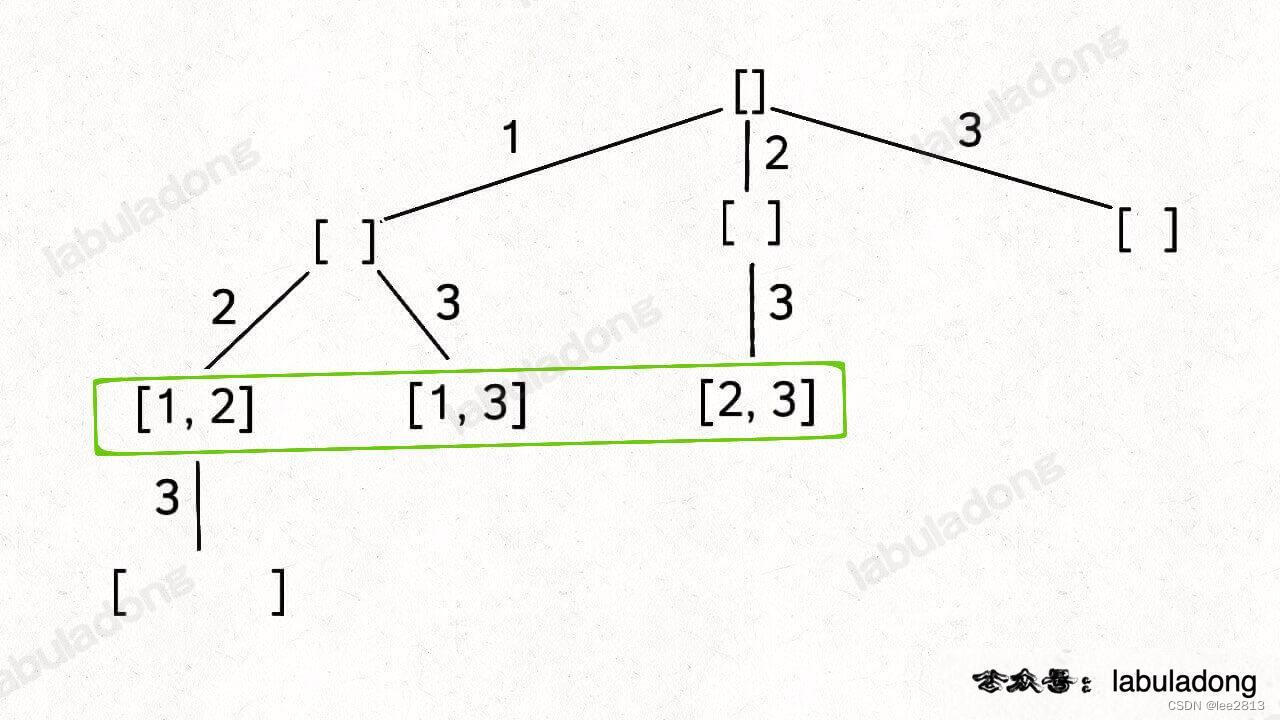
public: vector<vector<int>> res 存放结果vector<int> track 存放路径返回值 主函数名字(...){backtrack(nums, 0);return res;}backtrack(vector<int>& nums, int start){//满足条件，更新结果，结束本次递归res.push_back(track);//回溯算法框架for(int i = start; i < nums.size(); i++){//做出选择track.push_back(nums[i]);backtrack(nums, i + 1);//撤销选择track.pop_back();    }}

5.5 组合（元素无重不可复选）——返回递归路径

组合和子集是一样的：大小为 k 的组合就是大小为 k 的子集。
给你输入一个数组 nums = [1,2…,n] 和一个正整数 k，请你生成所有大小为 k 的子集。
还是以 nums = [1,2,3] 为例，刚才让你求所有子集，就是把所有节点的值都收集起来；现在你只需要把第 2 层（根节点视为第 0 层）的节点收集起来，就是大小为 2 的所有组合：

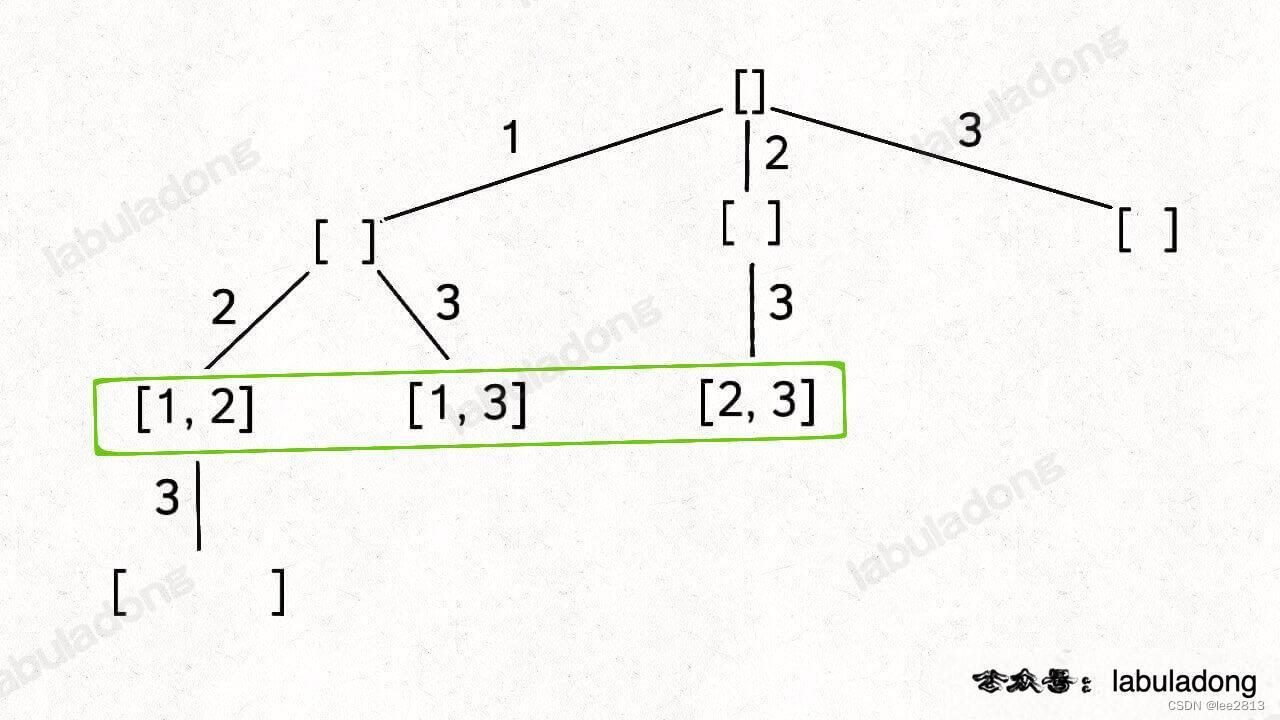
只需要稍改 base case，控制算法仅仅收集第 k 层节点的值，也就是判断当前路径中的元素个数 == k 时返回单次递归结果即可：

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码还未经过力扣测试，仅供参考，如有疑惑，可以参照我写的 java 代码对比查看。class Solution {
public:vector<vector<int>> res;// 记录回溯算法的递归路径deque<int> track;// 主函数vector<vector<int>> combine(int n, int k) {backtrack(1, n, k);return res;}void backtrack(int start, int n, int k) {// base caseif (k == track.size()) {// 遍历到了第 k 层，收集当前节点的值res.push_back(vector<int>(track.begin(), track.end()));return;}// 回溯算法标准框架for (int i = start; i <= n; i++) {// 选择track.push_back(i);// 通过 start 参数控制树枝的遍历，避免产生重复的子集backtrack(i + 1, n, k);// 撤销选择track.pop_back();}}
};

5.6 排列（元素无重不可复选）——可选列表

给定一个不含重复数字的数组 nums，返回其所有可能的全排列。
组合/子集问题使用 start 变量保证元素 nums[start] 之后只会出现 nums[start+1…] 中的元素，通过固定元素的相对位置保证不出现重复的子集。
排列问题本身就是让你穷举元素的位置，nums[i] 之后也可以出现 nums[i] 左边的元素，所以之前的那一套玩不转了，需要额外使用 used 数组来标记哪些元素还可以被选择。

class Solution {
public:// 存储所有排列结果的列表vector<vector<int>> res;// 记录回溯算法的递归路径list<int> track;// 标记数字使用状态的数组，0 表示未被使用，1 表示已被使用bool* used;/* 主函数，输入一组不重复的数字，返回它们的全排列 */vector<vector<int>> permute(vector<int>& nums) {used = new bool[nums.size()]();// 满足回溯框架时需要添加 bool 类型默认初始化为 falsebacktrack(nums);return res;}// 回溯算法核心函数void backtrack(vector<int>& nums) {// base case，到达叶子节点if (track.size() == nums.size()) {// 收集叶子节点上的值res.push_back(vector<int>(track.begin(), track.end()));return;}// 回溯算法标准框架for (int i = 0; i < nums.size(); i++) {// 已经存在 track 中的元素，不能重复选择if (used[i]) {continue;}// 做选择used[i] = true;track.push_back(nums[i]);// 进入下一层回溯树backtrack(nums);// 取消选择track.pop_back();used[i] = false;}}
};

算元素个数为 k 的排列，怎么算？
改下 backtrack 函数的 base case，仅收集第 k 层的节点值即可：

// 回溯算法核心函数
void backtrack(vector<int>& nums, int k, vector<vector<int>>& res, vector<int>& track) {// base case，到达第 k 层，收集节点的值if (track.size() == k) {// 第 k 层节点的值就是大小为 k 的排列res.push_back(track);return;}// 回溯算法标准框架for (int i = 0; i < nums.size(); i++) {// ...backtrack(nums, k, res, track);// ...}
}

5.7 子集/组合（元素可重不可复选）

刚才讲的标准子集问题输入的 nums 是没有重复元素的，但如果存在重复元素，需要进行剪枝，如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉，不要去遍历：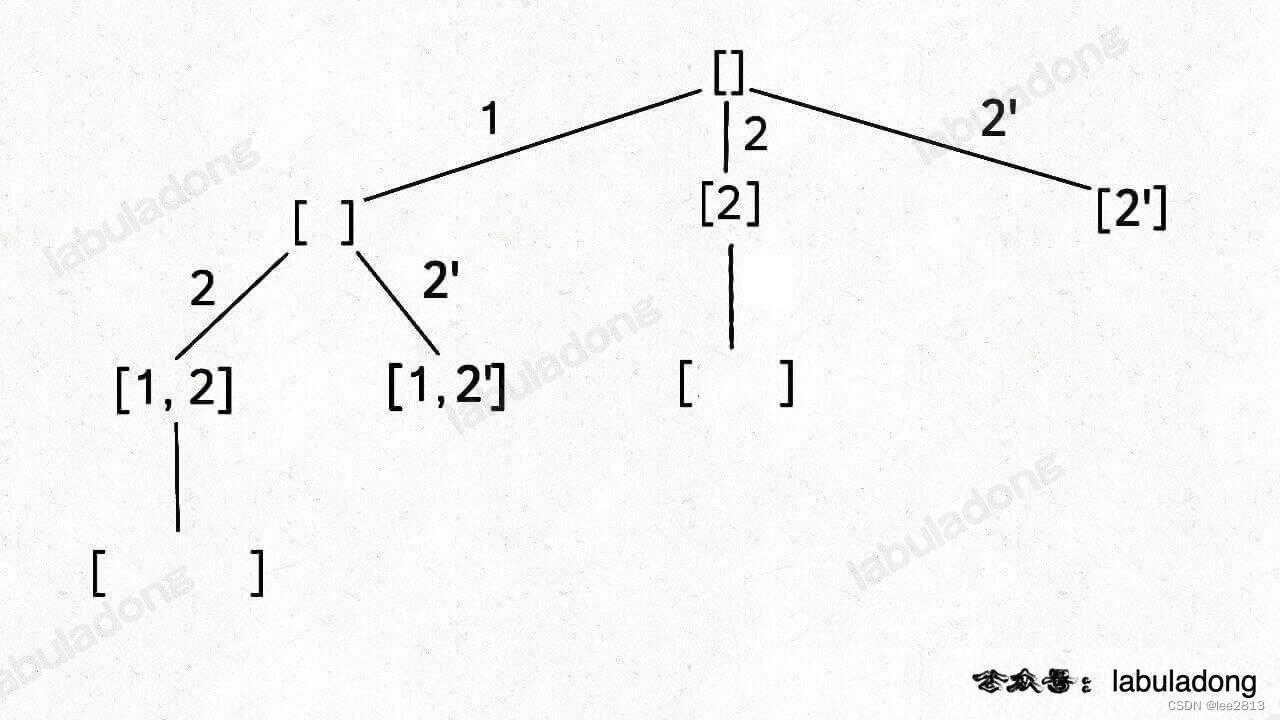

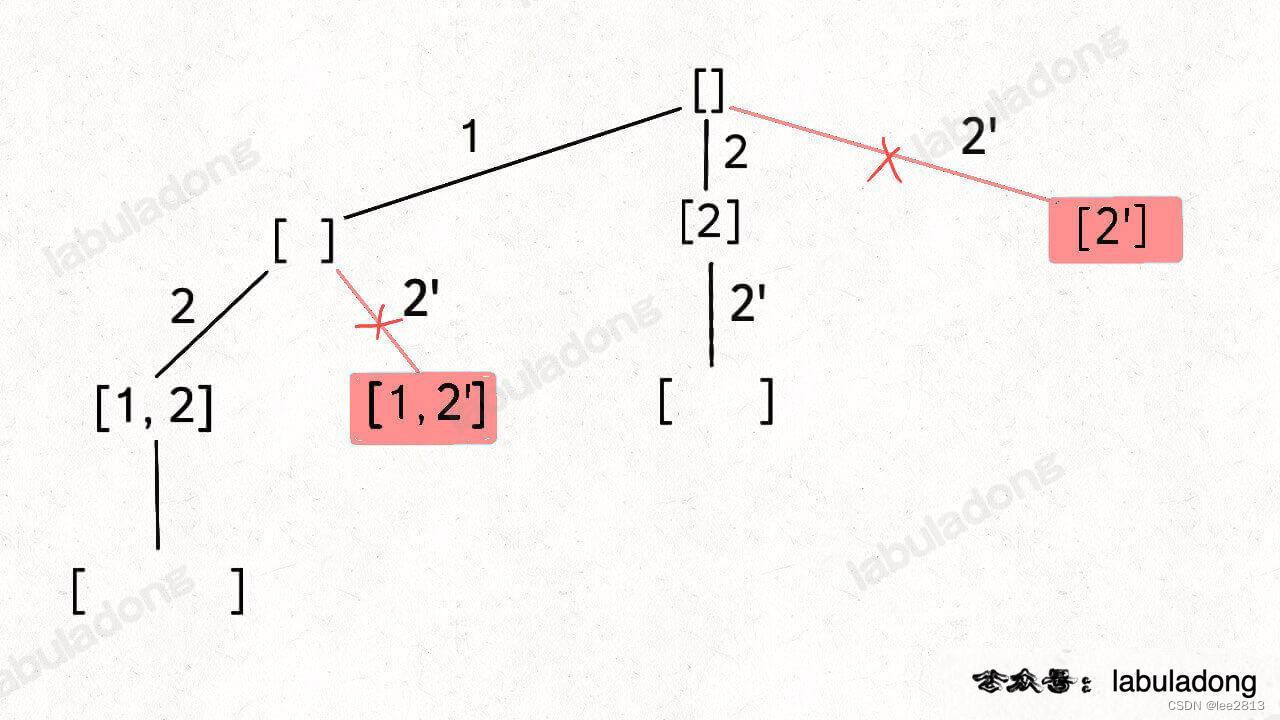
体现在代码上，需要先进行排序，让相同的元素靠在一起，如果发现 nums[i] == nums[i-1]，则跳过：

class Solution {vector<vector<int>> res; // 输出结果vector<int> track; // 搜索路径
public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end()); // 排序，让相同的元素靠在一起backtrack(nums, 0);return res; // 返回结果}void backtrack(vector<int>& nums, int start) { // start 为当前的枚举位置res.emplace_back(track); // 前序位置，每个节点的值都是一个子集for(int i = start; i < nums.size(); i++) {if (i > start && nums[i] == nums[i - 1]) { // 剪枝逻辑，值相同的相邻树枝，只遍历第一条continue;}track.emplace_back(nums[i]); // 添加至路径backtrack(nums, i + 1); // 进入下一层决策树track.pop_back(); // 回溯}}
};

这样剪枝，带重复元素的子集问题也解决了。

5.8 组合/子集（元素可重不可复选）

组合问题和子集问题是等价的。对比子集问题的解法，只要额外用一个 trackSum 变量记录回溯路径上的元素和，然后将 base case 改一改即可解决这道题：

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码还未经过力扣测试，仅供参考，如有疑惑，可以参照我写的 java 代码对比查看。class Solution {
public:vector<vector<int>> res;//记录回溯的路径vector<int> track;//记录 track 中的元素之和int trackSum = 0;vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {// 先排序，让相同的元素靠在一起sort(candidates.begin(), candidates.end());backtrack(candidates, 0, target);return res;}//回溯算法主函数void backtrack(vector<int>& nums, int start, int target) {//base case，达到目标和，找到符合条件的组合if(trackSum == target) {res.push_back(track);return;}//base case，超过目标和，直接结束if(trackSum > target) {return;}//回溯算法标准框架for(int i = start; i < nums.size(); i++) {//剪枝逻辑，值相同的树枝，只遍历第一条if(i > start && nums[i] == nums[i-1]) {continue;}//做选择track.push_back(nums[i]);trackSum += nums[i];//递归遍历下一层回溯树backtrack(nums, i+1, target);//撤销选择track.pop_back();trackSum -= nums[i];}}
};

5.9 排列（元素可重不可复选）

对比一下之前的标准全排列解法代码，这段解法代码只有两处不同：

• 1、对 nums 进行了排序。
• 2、添加了一句额外的剪枝逻辑。 if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) { continue; }
  标准全排列算法之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的；而如果固定相同元素形成的序列顺序，当然就避免了重复。
  进一步，如果 nums = [1,2,2’,2’‘]，我只要保证重复元素 2 的相对位置固定，比如说 2 -> 2’ -> 2’'，也可以得到无重复的全排列结果。

进一步，如果 nums = [1,2,2’,2’‘]，我只要保证重复元素 2 的相对位置固定，比如说 2 -> 2’ -> 2’'，也可以得到无重复的全排列结果。之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的；而如果固定相同元素形成的序列顺序，当然就避免了重复。

// 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {// 如果前面的相邻相等元素没有用过，则跳过continue;
}
// 选择 nums[i]

当出现重复元素时，比如输入 nums = [1,2,2’,2’‘]，2’ 只有在 2 已经被使用的情况下才会被选择，同理，2’’ 只有在 2’ 已经被使用的情况下才会被选择，这就保证了相同元素在排列中的相对位置保证固定。

两种剪枝方法对比：用绿色树枝代表 backtrack 函数遍历过的路径，红色树枝代表剪枝逻辑的触发

• !used[i - 1]
  

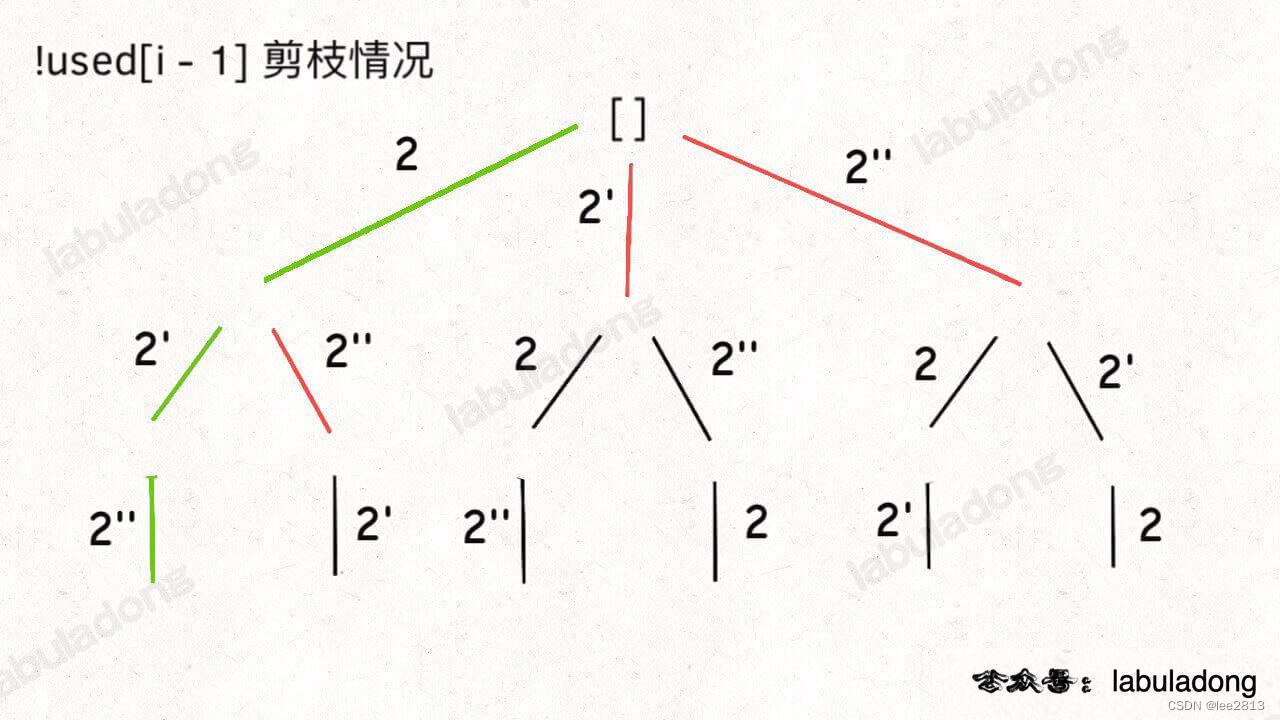
• used[i - 1]
  
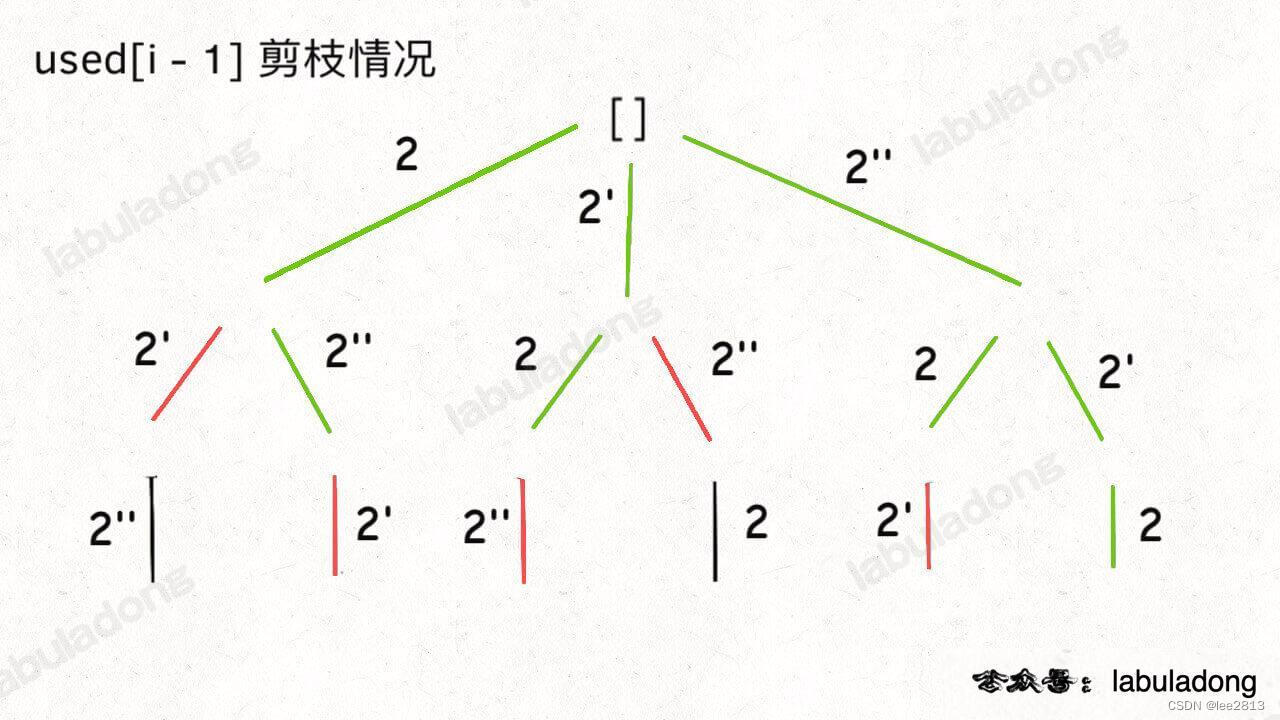
  !used[i - 1] 这种剪枝逻辑剪得干净利落，而 used[i - 1] 这种剪枝逻辑虽然也能得到无重结果，但它剪掉的树枝较少，存在的无效计算较多，所以效率会差一些。

5.10 排列/组合/子集问题区别

形式一、元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，backtrack 核心代码如下：

void backtrack(vector<int>& nums, int start) {// 回溯算法标准框架for (int i = start; i < nums.size(); i++) {// 做选择track.push_back(nums[i]);// 注意参数backtrack(nums, i + 1);// 撤销选择track.pop_back();}
}void backtrack(vector<int>& nums) {for (int i = 0; i < nums.size(); i++) {// 剪枝逻辑if (used[i]) {continue;}// 做选择used[i] = true;track.push_back(nums[i]);backtrack(nums);// 撤销选择track.pop_back();used[i] = false;}
}

形式二、元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次，其关键在于排序和剪枝，backtrack 核心代码如下：

sort(nums.begin(), nums.end());/* 组合/子集问题回溯算法框架 */
void backtrack(vector<int>& nums, int start) {//回溯算法标准框架for (int i = start; i < nums.size(); i++) {// 剪枝逻辑，跳过值相同的相邻树枝if (i > start && nums[i] == nums[i - 1]) {continue;}// 做选择track.push_back(nums[i]);// 注意参数backtrack(nums, i + 1);// 撤销选择track.pop_back();}
}sort(nums.begin(), nums.end());/* 排列问题回溯算法框架 */
void backtrack(vector<int>& nums, vector<bool>& used) {for (int i = 0; i < nums.size(); i++) {// 剪枝逻辑if (used[i]) {continue;}// 剪枝逻辑，固定相同的元素在排列中的相对位置if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue;}// 做选择used[i] = true;track.push_back(nums[i]);backtrack(nums, used);// 撤销选择track.pop_back();used[i] = false;}
}

形式三、元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次，只要删掉去重逻辑即可，backtrack 核心代码如下：

/* 组合/子集问题回溯算法框架 */
void backtrack(vector<int>& nums, int start, vector<int>& track) {// 回溯算法标准框架for (int i = start; i < nums.size(); i++) {// 做选择track.push_back(nums[i]);// 注意参数backtrack(nums, i+1, track);// 撤销选择track.pop_back();}
}/* 排列问题回溯算法框架 */
void backtrack(vector<int>& nums, vector<int>& track) {if (track.size() == nums.size()) {// 输出结果// ...return;}for (int i = 0; i < nums.size(); i++) {// 排除不合法的选择if (find(track.begin(), track.end(), nums[i]) != track.end()) {continue;}// 做选择track.push_back(nums[i]);backtrack(nums, track);// 撤销选择track.pop_back();}
}

六、BFS算法框架

问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离。

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {queue<Node> q; // 核心数据结构unordered_set<Node> visited; // 避免走回头路q.push(start); // 将起点加入队列visited.insert(start);int step = 0; // 记录扩散的步数while (!q.empty()) {int sz = q.size();/* 将当前队列中的所有节点向四周扩散 */for (int i = 0; i < sz; i++) {Node cur = q.front();q.pop();/* 划重点：这里判断是否到达终点 */if (cur == target)return step;/* 将 cur 的相邻节点加入队列 */for (Node x : cur.adj()) {if (visited.count(x) == 0) {q.push(x);visited.insert(x);}}}/* 划重点：更新步数在这里 */step++;}
}

七、动态规划问题

动态规划问题的一般形式就是求最值。
求解动态规划的核心问题是穷举。因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值。

列出正确的「状态转移方程」，才能正确地穷举判断算法问题是否具备「最优子结构」，是否能够通过子问题的最值得到原问题的最值。
另外，动态规划问题存在「重叠子问题」，如果暴力穷举的话效率会很低，所以需要你使用「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。

框架如下：

# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):for 选择 in 所有可能的选择:# 此时的状态已经因为做了选择而改变result = 求最值(result, dp(状态1, 状态2, ...))return result# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移 
for 状态1 in 状态1的所有取值：for 状态2 in 状态2的所有取值：for ...dp[状态1][状态2][...] = 求最值(选择1，选择2...)

性质一 重叠子问题（重叠子问题和状态方程）

1. 暴力递归
   斐波那契数列的数学形式就是递归的，写成代码就是这样：

int fib(int N) {if (N == 1 || N == 2) return 1;return fib(N - 1) + fib(N - 2);
}

递归树，很明显发现了算法低效的原因：存在大量重复计算，比如 f(18) 被计算了两次，而且你可以看到，以 f(18) 为根的这个递归树体量巨大，多算一遍，会耗费巨大的时间。更何况，还不止 f(18) 这一个节点被重复计算，所以这个算法及其低效。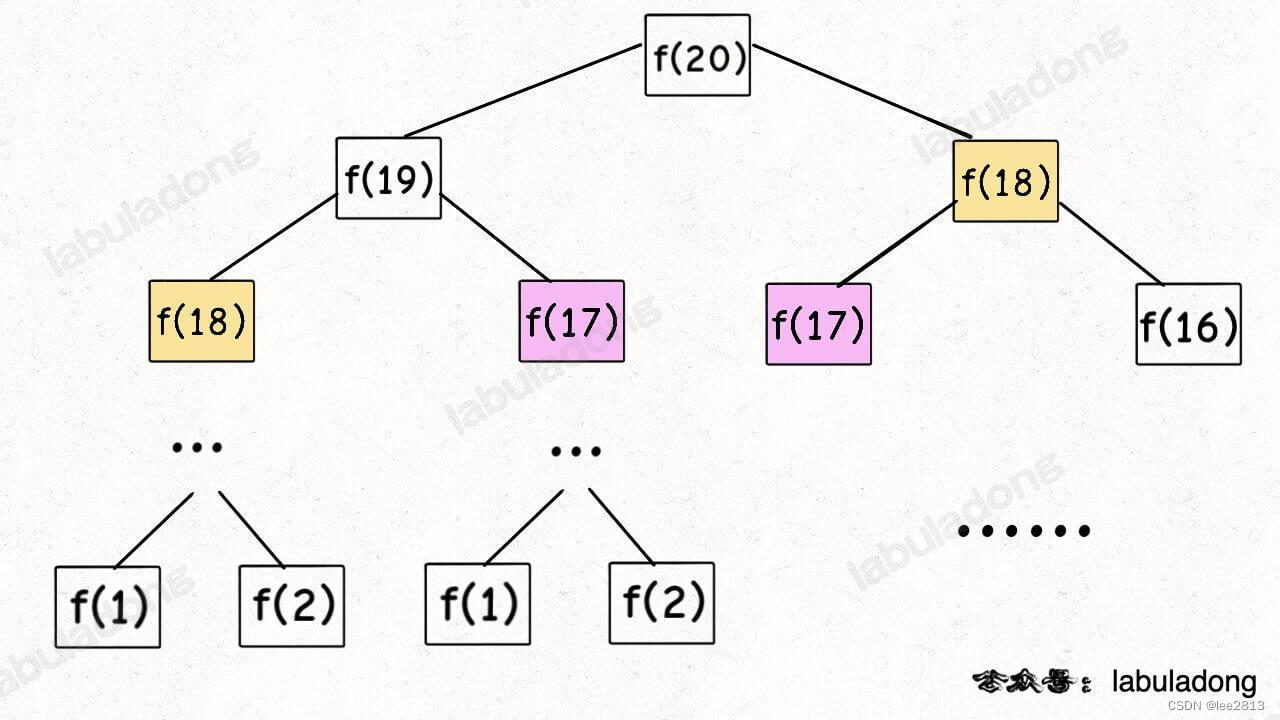
2. 带备忘录的递归解法
耗时的原因是重复计算，那么我们可以造一个「备忘录」，每次算出某个子问题的答案后别急着返回，先记到「备忘录」里再返回；每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。
使用一个数组充当这个「备忘录」，当然你也可以使用哈希表（字典）

int fib(int N) {// 备忘录全初始化为 0int memo[N + 1];memset(memo, 0, sizeof(memo));// 进行带备忘录的递归return dp(memo, N);
}// 带着备忘录进行递归int dp(int memo[], int n) {if (n == 0 || n == 1) return n;// 已经计算过，不用再计算了if (memo[n] != 0) return memo[n];memo[n] = dp(memo, n - 1) + dp(memo, n - 2);return memo[n];
}

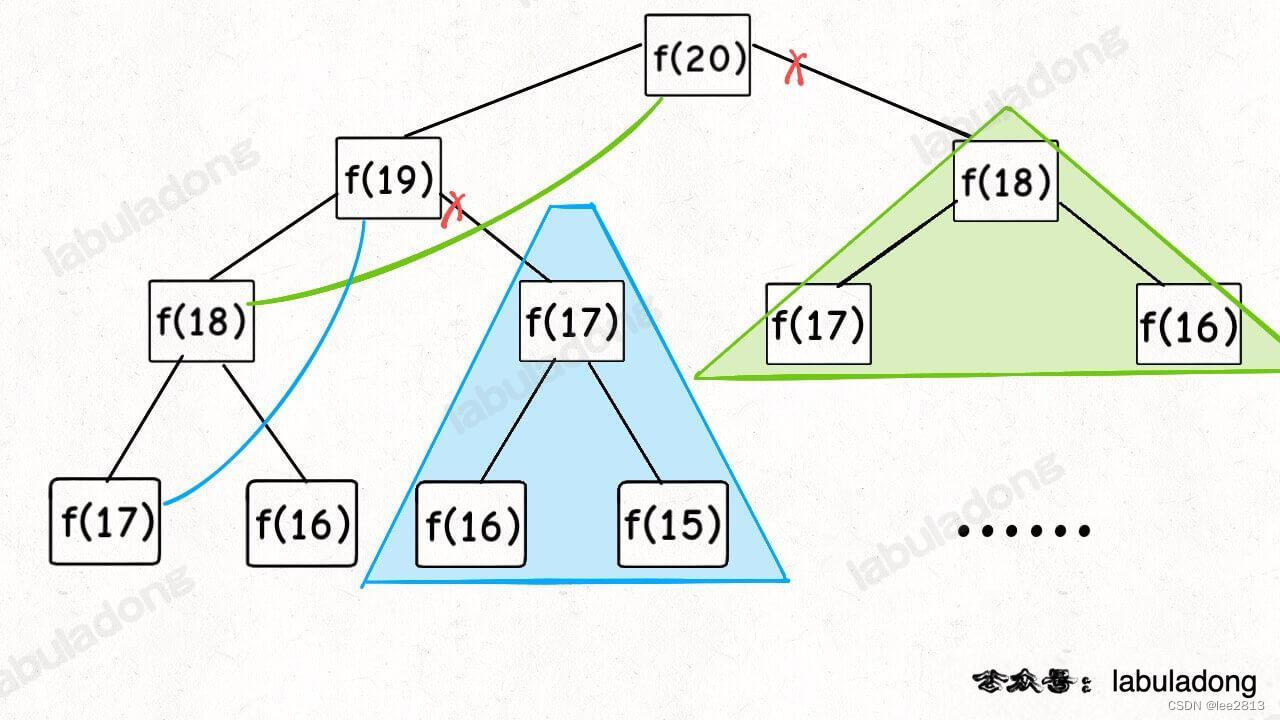
从一个规模较大的原问题比如说 f(20)，向下逐渐分解规模，直到 f(1) 和 f(2) 这两个 base case，然后逐层返回答案，这就叫「自顶向下」。

3. dp 数组的迭代（递推）解法
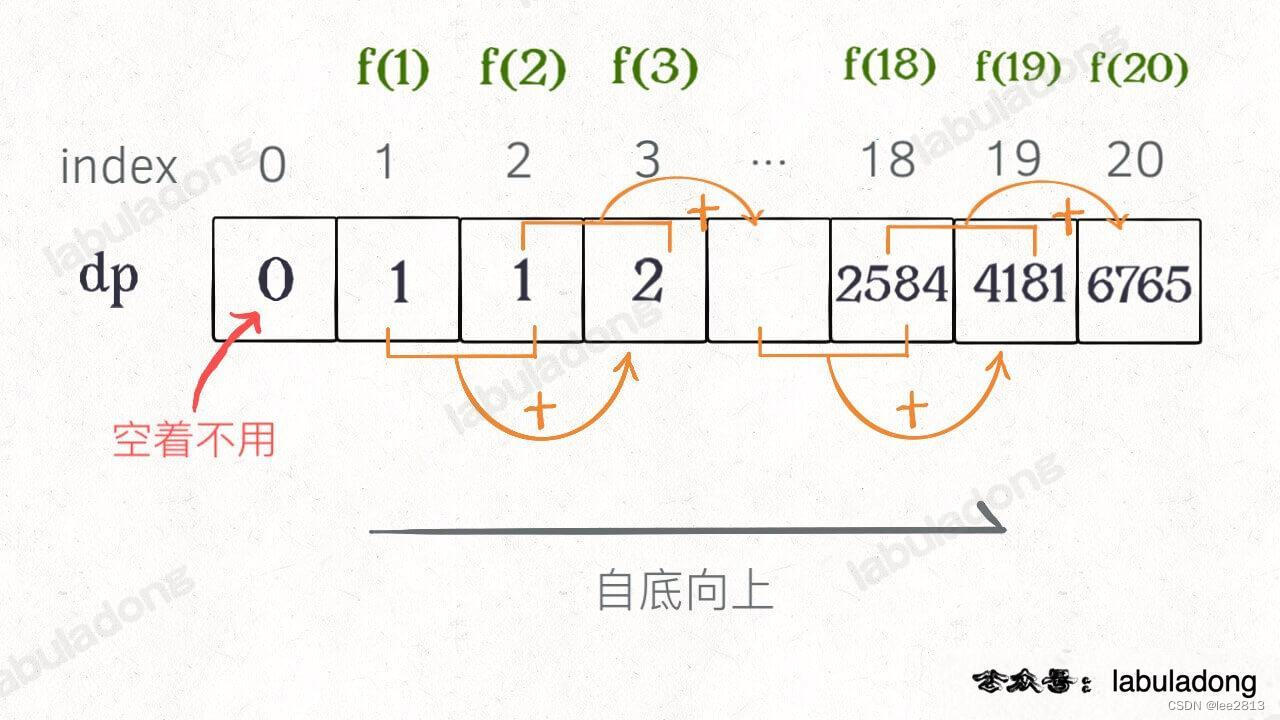
可以把这个「备忘录」独立出来成为一张表，通常叫做 DP table，在这张表上完成「自底向上」的推算

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码还未经过力扣测试，仅供参考，如有疑惑，可以参照我写的 java 代码对比查看。int fib(int N) {if (N == 0) return 0;int* dp = new int[N + 1];// base casedp[0] = 0; dp[1] = 1;// 状态转移for (int i = 2; i <= N; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[N];
}

引出「状态转移方程」这个名词，实际上就是描述问题结构的数学形式：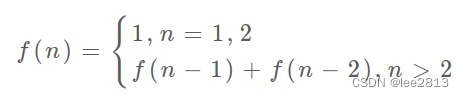
f(n) 的函数参数会不断变化，所以你把参数 n 想做一个状态，这个状态 n 是由状态 n - 1 和状态 n - 2 转移（相加）而来，这就叫状态转移，它是解决问题的核。动态规划问题最困难的就是写出这个暴力解，即状态转移方程。只要写出暴力解，优化方法无非是用备忘录或者 DP table，再无奥妙可言。

性质二 凑零钱问题（最优子结构）

1. 暴力递归

这个问题是动态规划问题，因为它具有「最优子结构」的。要符合「最优子结构」，子问题间必须互相独立。
假设你有面值为 1, 2, 5 的硬币，你想求 amount = 11 时的最少硬币数（原问题），如果你知道凑出 amount = 10, 9, 6 的最少硬币数（子问题），你只需要把子问题的答案加一（再选一枚面值为 1, 2, 5 的硬币），求个最小值，就是原问题的答案。因为硬币的数量是没有限制的，所以子问题之间没有相互制，是互相独立的。

2. 动态规划问题的一般思路：

• 确定 base case，这个很简单，显然目标金额 amount 为 0 时算法返回 0，因为不需要任何硬币就已经凑出目标金额了。

• 确定「状态」，也就是原问题和子问题中会变化的变量。由于硬币数量无限，硬币的面额也是题目给定的，只有目标金额会不断地向 base case 靠近，所以唯一的「状态」就是目标金额 amount。

• 确定「选择」，也就是导致「状态」产生变化的行为。目标金额为什么变化呢，因为你在选择硬币，你每选择一枚硬币，就相当于减少了目标金额。所以说所有硬币的面值，就是你的「选择」。

• 明确 dp 函数/数组的定义。我们这里讲的是自顶向下的解法，所以会有一个递归的 dp 函数，一般来说函数的参数就是状态转移中会变化的量，也就是上面说到的「状态」；函数的返回值就是题目要求我们计算的量。

3. 这样定义 dp 函数：dp(n) 表示，输入一个目标金额 n，返回凑出目标金额 n 所需的最少硬币数量。

class Solution {private:vector<int> memo;/*** memo 数组记录了 amount 对应的最优解，-666 代表还未被计算。* 因此，在计算 amount 对应的最优解时需要先查找 memo。*/int dp(vector<int>& coins, int amount){//1.确定Base Caseif(amount == 0) return 0; // 如果 amount = 0，那么硬币数量为 0if(amount < 0) return -1; // 如果 amount < 0，那么无解if(memo[amount] != -666) return memo[amount]; // 查备忘录，如果有最优解则直接返回int res = INT_MAX;/*** 在硬币数组 coins 中依次选取每个硬币。* 对于当前选择的硬币，计算是包含该硬币所需的子问题的最优解 subProblem。* 如果子问题无解，则直接跳过该硬币。* 在所有子问题中，选取最优解，并加上该硬币的数量。* 最终的结果 res 即为 amount 对应的最优解，该结果存入 memo 中。*///2.确定状态1： coin (原问题和子问题中的变量)for(int coin : coins){//3.定义行为(引起状态转移的行为): dp(coins, amount - coin)int subProblem = dp(coins, amount - coin);if(subProblem == -1) continue;//4.明确dp: 求最值res = min(res, subProblem + 1);}memo[amount] = res == INT_MAX ? -1 : res;return memo[amount];}public:int coinChange(vector<int>& coins, int amount) {/*** 初始化备忘录 memo，memo 数组的长度为 amount+1。* memo 数组记录了 amount 对应的最优解，-666 代表还未被计算。* 因此，在计算 amount 对应的最优解时需要先查找 memo，再根据结果进行计算。*/memo = vector<int>(amount + 1, -666);return dp(coins, amount);}
};

4. dp 数组的迭代解法，自底向上使用 dp table 来消除重叠子问题，关于「状态」「选择」和 base case 与之前没有区别，dp 数组的定义和刚才 dp 函数类似，也是把「状态」，也就是目标金额作为变量。不过 dp 函数体现在函数参数，而 dp 数组体现在数组索引：

dp 数组的定义：当目标金额为 i 时，至少需要 dp[i] 枚硬币凑出。

int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, amount + 1);// 数组大小为 amount + 1，初始值也为 amount + 1dp[0] = 0;// 外层 for 循环在遍历所有状态的所有取值for (int i = 0; i < dp.size(); i++) {// 内层 for 循环在求所有选择的最小值for (int coin : coins) {// 子问题无解，跳过if (i - coin < 0) {continue;}dp[i] = min(dp[i], 1 + dp[i - coin]);}}return (dp[amount] == amount + 1) ? -1 : dp[amount];
}

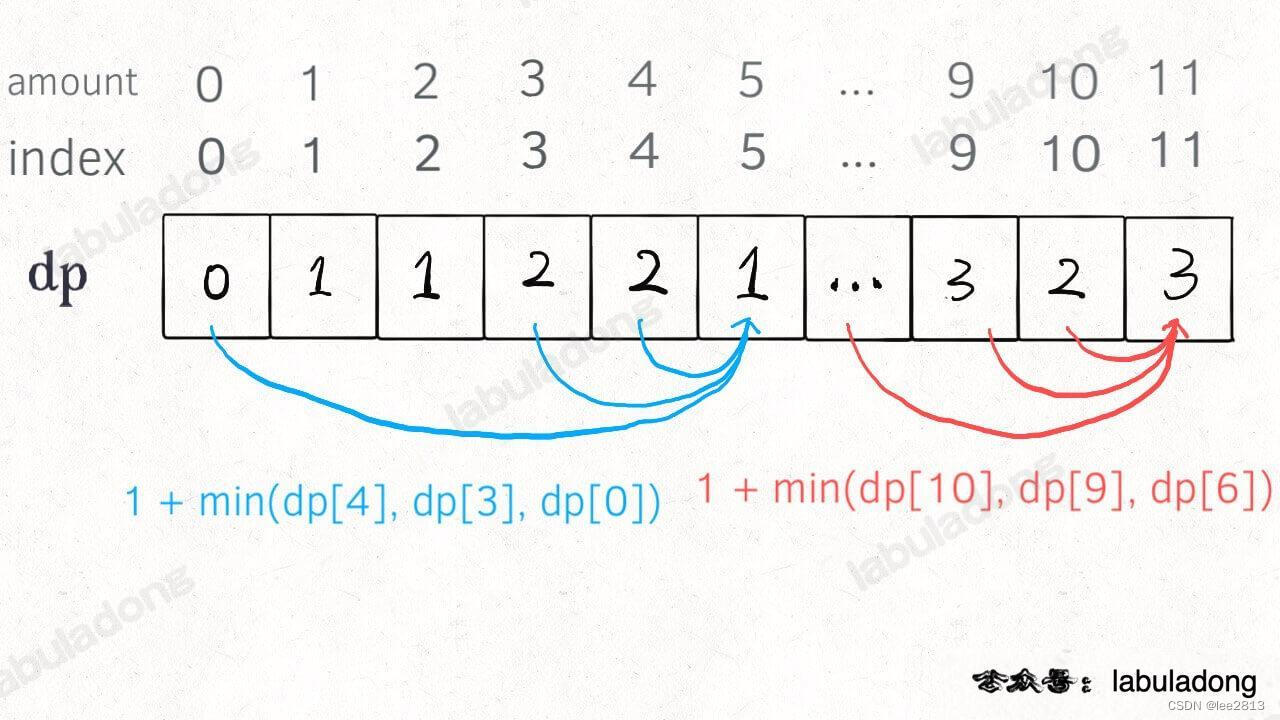
动态规划问题的一般思路

1. 列出状态转移方程，解决“如何穷举”的问题。

• 首先定义bace case
• 其次定义状态（子问题和父问题中变化的变量）
• 然后定义行为（进行子问题和夫问题之间状态转移的行为）
• 最后根据问题定义dp（求最值获其他）