列主元方法是一种用于求解矩阵逆的数值方法，特别适用于在计算机上实现。其基本思想是通过高斯消元法将矩阵转换为上三角矩阵，然后通过回代求解矩阵的逆。以下是列主元方法求解矩阵 $A$ 的逆的步骤：

步骤 1：初始化
构造增广矩阵 $[A|I]$，其中 $I$ 是 $n$ 阶单位矩阵。
步骤 2：列主元选择
对于第 $k$ 列（$k=1,2,\dots ,n$），找到列主元，即找到 $i_k$ 使得：
$$|a_{i_k,k}|=\underset{i\ge k}{\max }|a_{i,k}|$$
如果 $i_k\ne k$，则交换第 $k$ 行和第 $i_k$ 行。
步骤 3：高斯消元
对于每一列 $k$（$k=1,2,\dots ,n-1$），进行以下操作：

• 归一化第 $k$ 行的列主元：
  $$a_{k,k}\leftarrow \frac{1}{a_{k,k}}$$
• 更新第 $k$ 行的其他元素：
  $$a_{k,j}\leftarrow \frac{a_{k,j}}{a_{k,k}}\text{对于所有 }j\ne k$$
• 消去下方所有行的第 $k$ 列元素：
  对于所有 $i>k$，计算：
  $$m_{i,k}=a_{i,k}$$
  然后更新第 $i$ 行：
  $$a_{i,j}\leftarrow a_{i,j}-m_{i,k}\cdot a_{k,j}\text{对于所有 }j$$
  步骤 4：回代求解
  当矩阵 $A$ 被转换为上三角矩阵后，从最后一行开始回代：
  对于每一行 $k$（$k=n,n-1,\dots ,1$），进行以下操作：
• 归一化第 $k$ 行的最后一个非零元素（即对角线元素）：
  $$a_{k,k}\leftarrow \frac{1}{a_{k,k}}$$
• 更新第 $k$ 行的其他元素：
  $$a_{k,j}\leftarrow \frac{a_{k,j}}{a_{k,k}}\text{对于所有 }j\ne k$$
• 消去上方所有行的第 $k$ 列元素：
  对于所有 $i<k$，计算：
  $$m_{i,k}=a_{i,k}$$
  然后更新第 $i$ 行：
  $$a_{i,j}\leftarrow a_{i,j}-m_{i,k}\cdot a_{k,j}\text{对于所有 }j$$
  步骤 5：结果提取
  经过上述步骤后，增广矩阵的左侧变为单位矩阵，而右侧则变为了 $A$ 的逆矩阵 $A^{-1}$。提取右侧的矩阵即为所求的逆矩阵。
  需要注意的是，上述公式中的 $a_{i,j}$ 表示增广矩阵中的元素，包括原矩阵 $A$ 和单位矩阵 $I$ 的部分。在实际计算中，这些操作会同时应用于 $A$ 和 $I$，最终 $I$ 的位置会被 $A^{-1}$ 所取代。
  此外，如果在任何步骤中发现对角线上的元素 $a_{k,k}$ 为零或非常接近零，那么矩阵 $A$ 可能是奇异矩阵，无法求逆。在这种情况下，算法应该停止并报错。

Julia 代码

美化数据格式

using DataFrames
function pm(A,b)m,n=size(A); z=[]for i=1:n  st=iz=[z; "a:$st"]endfor i=1:nst=iz=[z;"b:$st"]endprintln(DataFrame([A b],z))
end             

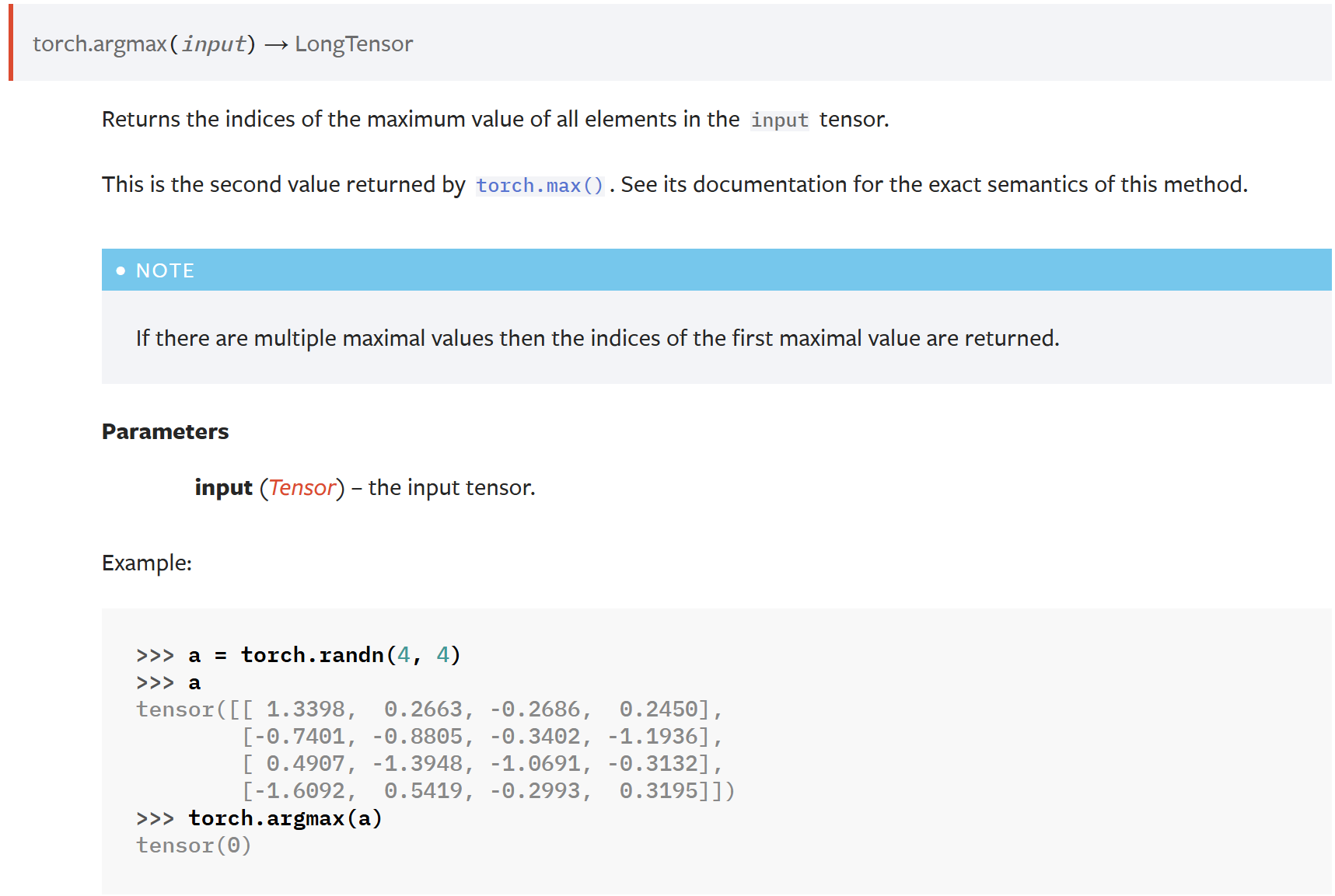
function luInv(A,par=false)n=size(A,1);T=typeof(A[1,1])A=copy(A); E = zeros(T,n,n); for i=1:n  E[i,i]=1//1  endif par pm(A, E) endif par println("化为上三角")  endfor i=1:n-1id=argmax(abs.(A[i:n,i])) # 寻找列主元 id=id-1A[i,i:n], A[i+id,i:n]= A[i+id,i:n],A[i,i:n]E[i,:], E[i+id,:] =E[i+id,:], E[i,:]for j=i+1:nc=A[j,i]/A[i,i]E[j,:]=E[j,:]-E[i,:]*cA[j,i:n]=A[j,i:n]-A[i,i:n]*cendif par pm(A, E) endendif par println("化为对角") endfor i=n:-1:2for j=1:i-1c=A[j,i]/A[i,i]E[j,:]=E[j,:]-E[i,:]*cA[j,1:i]=A[j,1:i]-A[i,1:i]*cendif par pm(A, E) endendIA=copy(E);for j=1:nIA[j,:] = E[j,:]/A[j,j]; A[j,j]=A[j,j]/A[j,j]endif par pm(A, IA) endreturn(IA)
end

举例

n=3;
A=zeros(Rational,n,n)
for i=1:n-1A[i,i]=0;A[i,i+1]=11//1;A[i+1,i]=7//1; 
end
A[n,n]=3//1;
IA=luInv(A,true)

结果