背景

完成软件的安装后，需要进行模型的编写。本篇将结合自己的学习心得，介绍一个简单模型的编写。

1 编写流程

参考材料链接link，材料里面包括“软件介绍、基本语法及案例分析”，提供的帮助很大；此处提出一个百度云链接link，提取码：b8wg。
下面将结合材料中提供的“案例二”，进行简明扼要地讲述，具体语法细节可参考上述材料。

1.1 集合声明

结构注意点：Sets是关键字，引领集合的声明；最后一个集合声明过后需要有分号结束，但集合之间不要分号。
语法注意点：i是集合名；goods是对集合的一个解释，可有可无；/ /之间内容是属性，其中BRD和MIL是属性名，中间以“,”隔开，;bread和milk是对属性的一个解释，可有可无。

Sets
i goods  /BRD bread, MLK milk/
h factors  /CAP capital, LAB labor/
;

1.2 参数赋值

1.2.1 标量声明

结构注意点：Scalars是关键字，引领标量的赋值；最后一个标量赋值过后需要有分号结束，但标量之间不要分号。
语法注意点：M1是标量名；maximum value是对标量的一个解释，可有可无；/ /之间内容是标量的数值。
PS:代码仅是举例方便理解，非本模型内容。

Scalars
M1       maximum value   /1E8/
M2       minimum value      /1/
;

1.2.2 一维向量声明

结构注意点：Parameters是关键字，引领一维向量的赋值；最后一个一维向量赋值过后需要有分号结束，但一维向量之间不要分号。
语法注意点：alpha是一维向量名；(i)是一维向量的下标；xxx是对一维向量的一个解释，可有可无；/ /之间内容是向量值，中间以“,”隔开，其中BRD和MIL是属性名，对应着此前声明的 i 集合。

Parameters
alpha(i)    xxx     /BRD 0.2, MLK 0.8/
px(i)   xxx    /BRD 1, MLK 2/
pz(h)  /CAP 2, LAB 1/
z(h)  /CAP 10, LAB 20/
;

1.2.3 二维向量声明

结构注意点：Table是关键字，引领二维向量的赋值；二维向量暂时知道的是仅能一个一个声明；声明完后，需要以分号结尾。
语法注意点：A是二维向量名；xxx是对二维向量的一个解释，可有可无；G1 F1等是向量的下标，需要有相应的集合声明以对应。
PS:代码仅是举例方便理解，非本模型内容。

Table A xxxF1      F2     F3      F4      F5
G1       1        2        3        4        5
G2       6        7        8        9       10
G3      11      12      13      14      15
G4      16      17      18      19      20 ;

1.3 变量声明

注意：目标值只能设置成Free类型。

1.3.1 变量关键字

1.3.2 举例

声明的是变量UU和正变量X(i)。

Variable
UUPositive Variable
X(i)

1.4 约束

1.4.1 约束声明

在编写约束之前，需要声明约束。
Equations是关键字，引领约束的声明；eqt是约束名称，ffggf是对eqt的描述，可有可无。

Equations
eqt   ffggf
obj   fgjg
;

1.4.2 约束编写

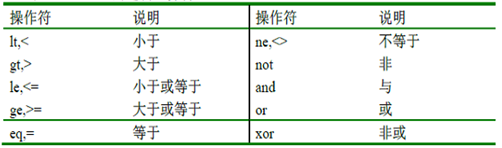
约束编写时，格式如下。编写中所需要的函数以及符号如下图所示。注：每个约束编写完成后均需要以分号结尾。

eqt..  sum(i, px(i)*X(i)) =e= sum(h, pz(h)*z(h));
obj..  UU =e= prod(i, X(i)**alpha(i));

1.5 模型建立及求解说明

分别通过如下两句语言实现。分别表示“将所建立的模型命名为HHmax”、“通过使用NLP模型求解器求解HHmax模型以得到UU的最大值”。

*Defining the model
Model HHmax /all/;*Sloving the model
Solve HHmax maximazing UU using NLP;

1.6 模型代码

* Definition of the Index Sets
Sets
i goods  /BRD bread, MLK milk/
h factors  /CAP capital, LAB labor/
;* Definition of Parameters
Parameters
alpha(i)  /BRD 0.2, MLK 0.8/
px(i)  /BRD 1, MLK 2/
pz(h)  /CAP 2, LAB 1/
z(h)  /CAP 10, LAB 20/
;* Definition of variables
Positive Variables
X(i)
;Variable
UU
;Equations
eqt   ffggf
obj   fgjg
;*Specification of equations
eqt..  sum(i, px(i)*X(i)) =e= sum(h, pz(h)*z(h));
obj..  UU =e= prod(i, X(i)**alpha(i));*Defining the model
Model HHmax /all/;*Sloving the model
Solve HHmax maximazing UU using NLP;

2 特别注意点

2.1 *和$的使用

2.1.1 *的使用

（1）以下两段代码等价，大家可以看到使用*的方便之处，具体可参考上面提供的文档。
PS:代码仅是举例方便理解，非本模型内容。

I      GG     /I1,I2,I3,I4,I5/  

I      GG     /I1*I5/  

（2）星号还有注释作用，可以看到1.6部分中以 ‘*’开头的语句，均为备注语句。

2.1.2 $的使用

$用于条件语句的表达。如下的语句表示“a在b大于1.5条件成立的情况下等于2”，如果条件不满足，则不赋值。
PS:代码仅是举例方便理解，非本模型内容。

a$(b>1.5)=2;

2.2 下标有限制范围的约束表达

2.2.1 举例1

注意：若约束表示多个式子，比如下图，其实这个约束表示K*I个式子，所以在声明时需要附上（K,I）。

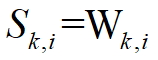
* Definition of variables
Equations
Con1(K,I)     for example
;
*Specification of equations
Con1(K,I)..      S(K,I)=e=W(K,I);

2.2.2 举例2

注意：若有加和符号，则用sum语句，格式为sum((下标)，变量)。

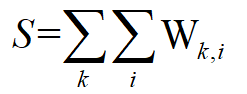
* Definition of variables
Equations
Con1 for example
;
*Specification of equations
Con1..      S=e=sum((K,I),W(K,I));

2.2.3 举例3

特别注意：对于这种有多个下标，但是只有一个下标有范围的，有三个注意事项。
第一个注意事项：类似于2.2.1，在声明时需要附上（K,I）；
第二个注意事项：由于i和i1共用同一个集合I，因此需要加上ALIAS，相当于复制I；
第三个注意事项：sum((下标)，变量)加和时，需要在下标后附上对i1的限制。
具体见代码。

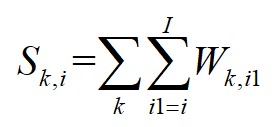
Set I;
ALIAS(I,IL);
* Definition of variables
Equations
Con1(K,I) for example
;
*Specification of equations
Con1(K,I)..      S(K,I)=e=sum((K,IL)$(ord(IL) ge ord(I)),W(K,IL));

此处引出两个额外符号，ord()和ge，其中ord(I)的意思“得到此时的I在集合中的排序”，ge的意思是“大于等于”，因此“ord(IL) ge ord(I)”的意思就是“在集合中，排序大于I的IL”。

3 模型求解

3.1 解决方案

模型的求解当然要利用求解器了（需要购买）。首先通过“File——Options——Slovers”，可以看到自己可使用求解器情况，如下图。“Demo”表示可以使用，“Full”则表示能够完全使用。

对于没有许可证的同学，此处提供一个贴吧里的解决方法，链接link，通过下载链接中的文档，获得许可证，并且在修改完自己系统时间后，通过“File——Options——Licenses”选择许可证，即可使用。（PS:本人未尝试，仅贴出来一种可能的解决方案）。

3.2 求解结果

本文算例求解结果如图所示，x(1)=8，x(2)=16，目标值UU=13.929。

4 总结

至此，利用GAMS进行模型的编写及求解已完成。

【整理不易，转载请注明出处和相关链接，否则必究！】