仿真是以博主学校为原型建模的哦，其实不管是哪里都大同小异，代码是我和我一个组员一起写的，比较简单就直接仍最后面了，大家多多点赞收藏支持一下啦！博主本身不是做和图有关的问题的，这只是一个结课论文，所以有些不对的地方大家都可以大胆指出。

标题：基于多参数随机过程的疫情仿真与多因素决策及博弈分析

问题背景：
自新冠疫情初次爆发至今已有近两年半时间，期间疫情形式跌宕辗转，一直无法真正平息。对于在校学生而言更是因为频繁的封校以及核酸检查叫苦不迭，学校所进行的决策也是粗暴的定期核酸以及对于有密接或者次密接的人进行直接隔离，但实际上这种决策在纯经济角度是浪费了大量的人力财力以及时间。所以我们想要通过这篇文章，能够尽量的仿真疫情在学校（或其他较封闭体系）的传播形式，结合戴口罩，打疫苗，核酸频率，校外输入，基本传染数等多因素考虑找到整体疫情防控与开销的最优解,并针对新冠病毒一直变异的现状，基于病毒进化导致感染强度的改变引入人与病毒的博弈行为。

关键词：
传染病仿真，博弈论，随机过程，最优化

1.引言
大多例如SI, SIR, SIRS, SEIR [1,2,3,4]的传统传染病模型都是基于图的传播，最多会考虑到隔离，即切断结点的边，但这样就固定了人与人接触的情况。这种普通的仿真方法更多的是基于纯理论模型的方面来进行某种传染病的模拟，与现实世界中的疫情传播往往大相径庭，尤其是学校这种所有人都有概率接触，并且接触概率完全随机的场景。

所以本论文放弃将人与人间接触的情况用固定的图模拟，而转用人出现的场景完全随机，并以欧氏距离判断是否接触的方式来进行病毒的传播（类似于随机图），当且仅当每个人回到宿舍时才会与舍友，即临近人员产生固定解除关系。然而这种模式大大的复杂了病毒传播方式以及决策方法的实现，根本无法从纯数学的角度提出解析解，故而只能通过计算机程序仿真的方式模拟传播形式，找到近似最优解。而又因为例如人的行为（去到的场景和地点）以及免疫力完全随机，但过程完全相同，故我们可以认为此仿真为一个多参数随机过程，所以本篇论文仅通过仿真中改变例如核酸频率与隔离（或采取治疗）人数比例对整体疫情防控的影响来进行初步决策拟定，最终评判条件为一个月内核酸费用，隔离费用以及治疗费用的总和，不考虑死亡情况（改为增加所需治疗费用）。

虽然传播的方式和考虑的因素与其他方法不尽相同，但对于感染者的类别，我们采用类似的类别方法，分为：
1.N类，普通人（Normal），可以感染病毒并携带病毒，但有一定的免疫力可以自主康复。
2.Im类，免疫者（Immunity），完全不会感染病毒。
3.In类，感染者（Infected），已经被感染的人，并不会自己恢复
4.R类，恢复者（Recovered），中途自主康复的人，但仍然可能会被再次感染。
5.IS类，隔离者（Isolated），感染后被拉去隔离的人，中途可能会受到治疗康复，或者自主康复，以后不会再次被感染。

注：本文认为N类人可以携带病毒但通过免疫力每天晚上会自己康复一定程度，到感染概率p<0.1时则会完全恢复成为R类，但如果到爆发期（每7天一次）仍然p>0.1但不是感染者(其中感染者为当天感染概率p>0.8我们直接改变其感染概率为1)，此时我们便会让这些人以其感染概率作为标准让其变为感染者In类。

本文将基于以上所说模式以及人群类别，综合分析戴口罩，打疫苗，校外输入，群体免疫，交叉感染，R0（基本感染数）[5]，核酸频率，隔离方式以及是否治疗等九种因素对整体疫情的影响来考虑对应决策以及最低的控制疫情所需成本。

其中存在人与病毒的博弈：
随着疫情的控制，病毒的传染强度会随感染人数的变少而增强（类似超级细菌），但变异条件同样需要时间，我们设定变异周期与爆发周期一致（均为一周），最终评判为第30天，所以一共可能变异4次。

所以本文的贡献主要有以下几点：
1.用一种全新，切合实际但十分简单的方式模拟疫情传播。
2. 定义新的人群类别假设—NTIR（其中T为Triple）。
3. 考虑多种因素对疫情的影响并分析最优对策。
4. 考虑R0变化，对传染病模型引入博弈行为，更贴近现实现状。

2.疫情建模与方法算法描述
2.1基本方法（迭代）
我们将问题场景定在我们学校的某一个校区，故一共存在如下七个场景：
宿舍,图书馆,教室,操场,餐厅A,餐厅B,散步区域

其中我们认为每个人一天有5次迭代，前4次会随机出现在上述7个场景中，而第5次则一定是回宿舍（睡觉）。场景大小为1500x1500m，而每个场景中的人会随机出现在其中的某个坐标上：

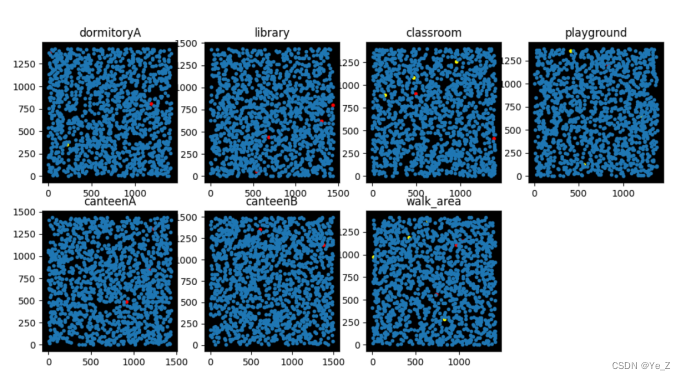
Figure 1: 迭代状态图，设感染概率为p，其中红色为已感染（p=1），黄色为携带者（0.8>p>0.1），蓝色为健康（p=0），其中携带者也可以认为是无症状感染者。

只要结点携带感染概率则认为会传播病毒，其传播方式为以该结点为圆心，以R为半径，距离该结点为0-R的结点认为是密接，距离为R-2R的认为是次密接，具有不同的感染概率，注意寻常所说的R0为基本感染数，但我们这里将其具体化为感染强度，R0=ln(2*R),故感染概率为分段函数，如下所示公式(1)：

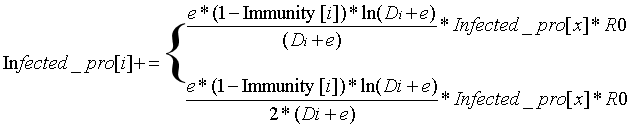
上式为密接感染概率，下式为次密接感染概率，其中x代表圆心结点序号，i代表该结点序号，Di表示该节点离圆心的距离，e为自然常数。（乘e与加e是为了保证函数在dist上单减且在0处取到极大值，即认为距离越近，感染概率越大）

而每天第5次迭代（即回宿舍）后，其他人会被同宿舍的人直接感染，5个人一个宿舍，同一宿舍的人感染概率会变为其中感染最严重人的感染概率，即对于每5个结点都有公式(2)：

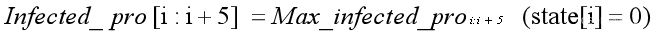
其中state表示状态，我们定义state=0为未感染，state=1为感染，state=2为隔离中，所以只有状态为0的人会被感染。

同化后便会开始恢复，我们每个人初始化了一个免疫概率Immunity[i]，恢复过程便为现在的感染概率乘以免疫概率，即如公式(3)：

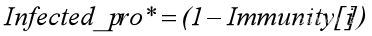
以上便是常规的，无其他因素的迭代，我们后续的所有实验都是通过此基本模型实现。注意其中感染概率最大为1，如果迭代途中大于1了我们就向下取整为1。

2.2疫情爆发设置
我们设定疫情7天一爆发，通过简单的随机数模拟爆发情况，即在第七天恢复后，对于每个存在感染概率的人，即Infected_pro > 0的人进行选取0-1之间的随机数，如果随机数小于p该结点就感染，反之则感染率清空：

2.3参数设置
我们初始化三个列表来记录结点状态，一个为infected_pro，记录感染概率，范围0-1，初值为0，第二个为immunity，记录免疫概率，范围0-1，初值随机0.5-0.8。第三个为state，记录结点状态，0为未感染，1为感染，2为隔离，其中隔离状态不会参与后续迭代过程。然后就是传染半径，根据实验过程我们发现当R设置为合适的大时候才会存在将已感染结点隔离后仍然会爆发（无校外输入），如果R过大即使每天做核酸也无法抑制住疫情，所以我们取一个较为合适的值，R=10，其中初始感染者我们设定的期望为5人。

2.4核酸设定
我们认为做核酸的消费是以人为单位，如一个人核酸需要60元，当天就可以出结果，并且测出的结果可以直接得到感染概率，所以我们是通过每个人的感染概率来决定是否隔离，但因为每个节点可以自我恢复，所以这个隔离阈值有待商榷，如果阈值太高，我们只将感染的人隔离，那大概率会再次爆发，后续爆发消费会很高，但是如果阈值太低，其实有很多人可以自己恢复，浪费经济。

2.5打疫苗和戴口罩的影响
打疫苗的效果很好实现，我们直接把初始化的immunity增大即可，从0.5-0.8转变为0.6-0.9，而戴口罩则可以在感染概率(公式1)中乘以额外免疫概率，如乘以新免疫概率Immunitymask = 0.6。
.
2.6校外接触的影响
我们每天以期望为10个人的概率抽取设置为感染，同时state设置为1，认为因为校外接触导致感染。

2.7群体免疫
群体免疫即为设定一定比例的人Immunity为1，通过大部分不会感染导致剩下的一小部分人也不会被感染。

2.8病毒进化与博弈论
我们认为病毒进化周期与疫情爆发周期相同，设定为7天，并且进化概率与现感染人数与走势相关，所以我们需要考虑每天感染人数的多少以及到爆发当天的感染人数来安排做核酸的频率以及带走人数的阈值，这样才不会导致病毒强度急剧上升但感染人数降低导致误判以致持续后续成本过高。

2.9隔离与治疗费用
我们认为隔离费用为一人2k元，治疗费用为1人2w或3w元，隔离为依靠自己自愈力恢复后按照感染概率变为感染者或是恢复者，此时感染者就必须要被治疗，花费3w元，但如果一开始就选择治疗则只需要2w元恢复。

3.实验分析
3.1基本方式迭代
所谓基本方式迭代，即不考虑任何附加条件，任由疫情扩散和人员自身恢复：
本次分析为总结点1w人，初始感染者7人：

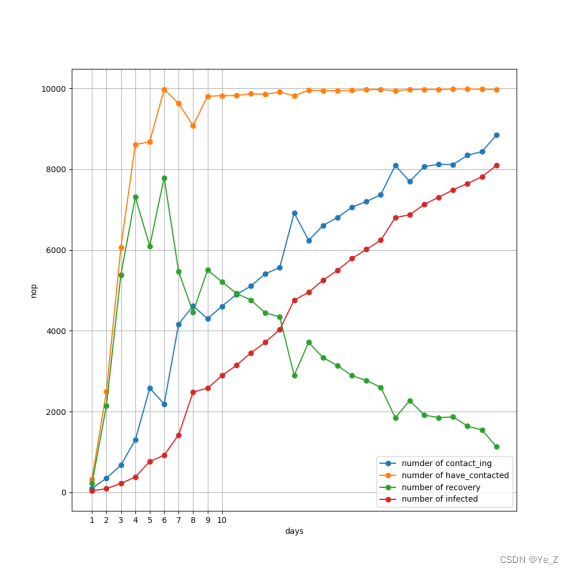
Figure2： 自然状况下感染趋势图

其实非常好理解与分析，接触者人数一定是指数增长达到阈值，然后因为一开始的接触者大多都是很小的感染概率，通过恢复几乎都会恢复，但随着感染概率的积累以及真正感染者人数的增多，大部分人都无法恢复，所以绿色(恢复者)曲线持续下降，蓝色（携带者）曲线持续上升，而红色（感染者）曲线先平缓，然后陡增，最后几乎线性增加是因为一开始接触者都恢复了，所以上升趋势是次线性的，而等到积累一定程度的时候，免疫力较低的人会被快速感染，所以呈现了指数型暴增，后续因为剩下的多为免疫力高的人，所以被感染者增加的速度变得比较缓慢，呈线性增长趋势。

3.2 戴口罩与打疫苗对疫情的影响
戴口罩我们认为传播的时候有0.2的概率可以阻断传播，即对公式1乘以0.8：

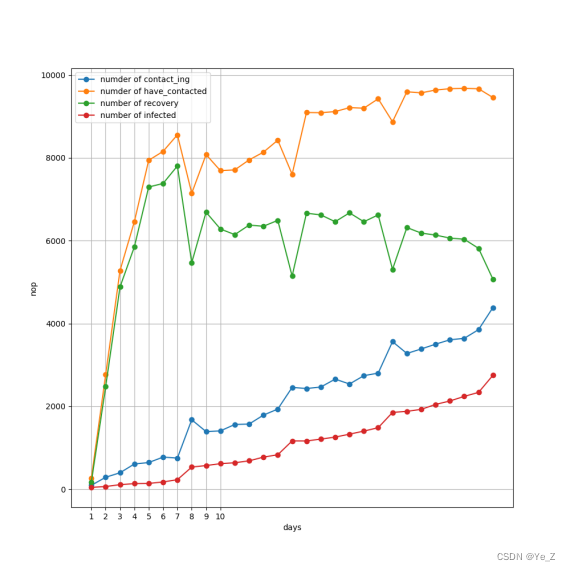
Figure3：戴口罩情况下感染趋势图。

可以看到这里我们感染趋势变为次线性的了，但后期仍然回归线性，因为感染的人数多了，基数大导致交叉感染，口罩的防护作用渐渐变低，其中陡增是因为疫情爆发（7天为周期）。

然后就是打疫苗，我们把打疫苗转化为免疫概率增加，从0.5-0.8变为0.6-0.9：

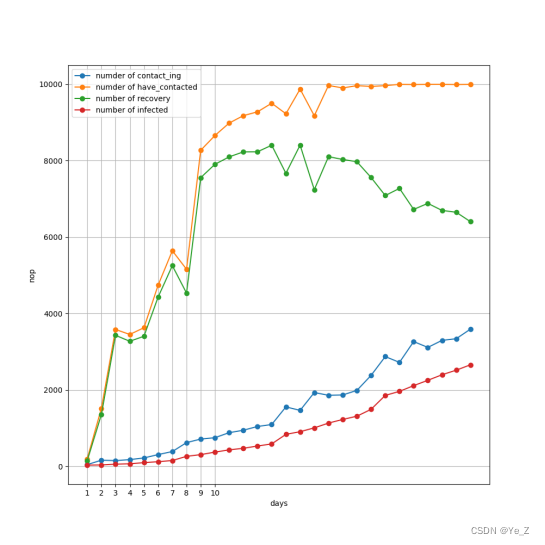
Figure4： 打疫苗情况下感染趋势图。

可以看到打疫苗的情况和戴口罩大致相同，但感染过程更加平缓，因为对于寝室感染等各种交叉感染，提高免疫力都可以高效的防止疫情的传播，并且打疫苗也可以有效防止病毒大规模爆发，可以看到爆发期和普通增长趋势也是类似的。

3.3做核酸
我们设定做核酸可以查取所有人的感染概率，（并且我们不采取优化方式，例如一个寝室查一般，因为优化方法太多，我们主要做整体分析，每个人都要做），所以做核酸主要是考虑隔离阈值的采取，以及核酸频率的采取。

3.3.1 无校外输入情况下做核酸
实验表明，在无病例输入的情况下，两天做一次核酸最为合适（因为我们假定不知道什么时候才知道有病例，所以需要等一段时间存在密接者后开始测定，即第1天不测，否则第一天测完核酸隔离就不需要后续了），这种情况下可以有效的抑制疫情爆发和感染人数增长，并且充分利用人的自愈能力，减少隔离人数，并在第11天时就阻断了疫情，后续存在级联现象，所以可以停止核酸检测，最终把花费从隔离787人变为总共隔离459人，共减少328人的隔离与治疗费用，但增加4次核酸费用，通过花费估算，不考虑非感染者也直接治疗，可以至少减少50w左右的消耗，其中隔离阈值为0.4最好。

3.3.2 有校外输入的情况下做核酸
因为我们明知可能有校外输入，我们直接考虑一天一次核酸和两天做一次核酸（三天一次根本无法抑制），两天一次结果如下：

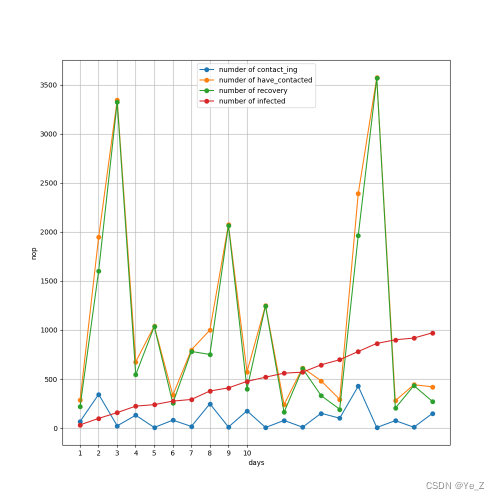
Figure5：有校外输入情况下两天一次核酸感染趋势图。

可以看到感染情况急剧震荡，因为校外输入导致疫情根本无法平息，所以我们在没做核酸的那一天，已存在的携带者和新的感染者交叉感染，使疫情爆发，但第二天拉去隔离后感染者就又变少，但总感染者到30天结束的时候已经达到了1421人，并且隔离阈值最好设置为0.2，否则感染情况更严重。
每天做核酸：

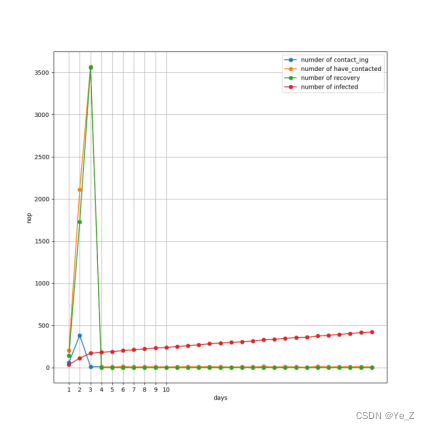
Figure6:有校外输入情况下每天一次核酸感染趋势图。

可以看到每天核酸可以即时的捕捉到校外输入，所以只存在校外输入的人被拉去隔离治疗，因为校外输入是以固定期望，所以感染人数呈线性增长，最终30天结束为432人

注：核酸为每天晚上做，所以第二天早上在未接触前就可以得到结果，此时校外接触的人可以直接被拉去隔离或者治疗。

综上考虑，相比于两天一次核酸，每天做核酸一共减少了近1k的感染人数，但多了一倍的核酸成本，合计总共节约约200w的成本费用。

3.4 群体免疫

群体免疫在2.7中已有介绍，即按比例将人免疫力设为1（完全不会感病），剩下的还是随机0.5-0.8的免疫力，按照群体免疫理论[6],群体中有百分之70-80的人具有免疫疾病的效果，则可以达到群体免疫。在这里我们考虑有校外输入的群体免疫和无校外输入时的群体免疫两种情况。
3.4.1无输入群体免疫：
很可惜，将免疫比例设置为80时并无法实现群体免疫，但比例达到90时，基本可以实现群体免疫：

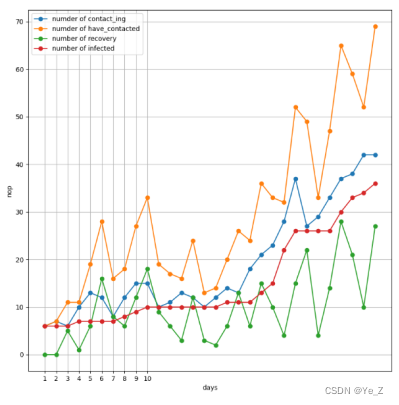
Figure7：无校外输入群体免疫感染趋势图
可以看到不采取任何措施，30天结束后仅感染36人

3.4.2有输入群体免疫：

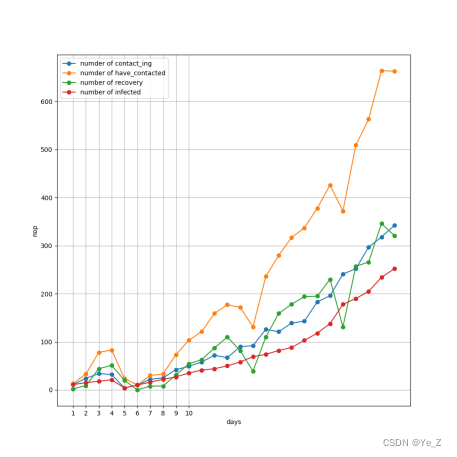
Figure8： 有校外输入群体免疫感染趋势图

可以看到最开始接触者非常少，因为免疫者多，不携带病毒，但后面因为陆续输入，感病者持续增加，群体免疫失效。

综上，群体免疫的作用效果是因为免疫者比例大，隔绝感染者与易感者，并极大的减少了交叉感染的风险，但对于有校外输入的情况，即使免疫者达到95%也无法组织疫情在易感者中的传播，因为结点间的交互过于频繁，等感染者达到一定程度后群体免疫失效，病毒仍会在易感者中传播。

3.5 病毒进化引起的博弈分析
我们认为病毒会随着时间和感染人数的变化而变异，周期与疫情爆发是相同的。
本实验只考虑有校外输入的情况，因为如果没有，在病毒变异前就已经全部控制下来了，并且无需后续花费。其感染能力变化为：

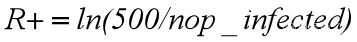
即为R增长的值与现感染人数成反比（nop_infected为现在感染的人数），并且代价为5个普通病毒转变为一个变异病毒。
可以看到现在如果两天一次核酸：


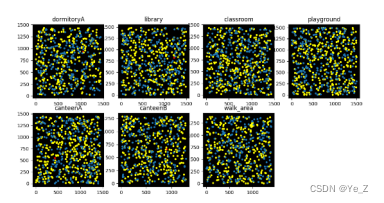
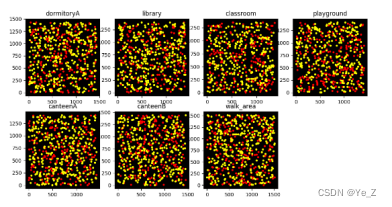
Figure9：病毒变异后一天感染变化，蓝色为未感染者，黄色为携带者，红色为感染者。

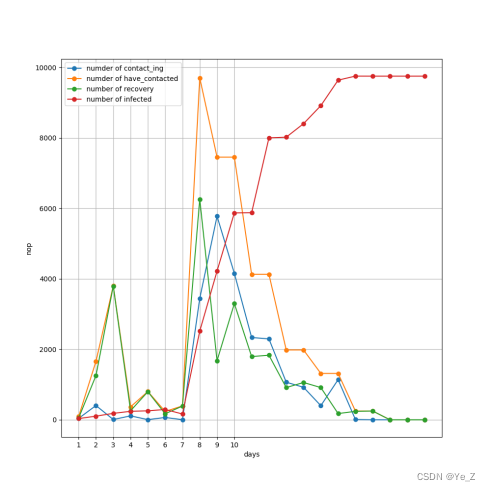
Figure10：引入病毒变异后两天一次核酸感染趋势图

可以看到未变异时两天一次核酸还可以控制住疫情规模，但加入变异后，两天一次核酸，在第16天左右就基本全军覆没，即使病毒变异存在代价（虽然代价不是很大），但总体根本无法抑制。

所以综合考虑，即使增加病毒变异代价或者减少R增加程度，也只能通过从根源抑制，即每天做核酸直接把输入病例隔离，杜绝接触！

3.6 隔离或是治疗的决策商定
我们在2.9中已经设定好隔离与治疗的费用，以及设定，所以其实最终决策就是对于同一批人，直接治疗的阈值设为多少会得到最小的成本。
其实很简单，我们直接考虑单个个体即可，感染概率为p，免疫概率为q，则隔离后康复的概率为p*(1-q),感染的概率为p*q，所以当如下情况时：

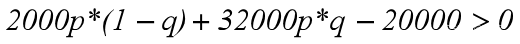
我们选择隔离而不是直接治疗，其中取免疫概率均值q=0.65，带入则为求：

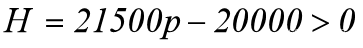
可以看到函数明显单调递增，所以我当p=100/101时，H=0，所以我们在p<0.93时，选择隔离，大于0.93时则直接治疗，而又因为我们感染概率大于0.8时直接认为感染，将概率赋为1，所以综上，感染者全部直接治疗，携带者全部隔离等待自然恢复即可。

4.总结
以上讲述了我们整个疫情传播的建模方法，并且分析了各种，例如戴口罩，打疫苗，病毒进化等因素对决策的影响，其实结合实际情况（不封校），还是2-3天一次核酸最好，毕竟实际情况更多还是要从人文方面考虑而不仅仅是消费成本。否则结合新冠实际的传播强度，并结合本校策略，戴了口罩并打疫苗，抑制出校，其实一周一次都显得比较频繁。但是为了防止万一，我们最好还是按照学校和政府防疫政策来做，不要私自隐瞒行程并且轻易不带口罩，因为从实验来看，如果遇到变异性病毒（如奥米克戎）很容易全军覆没。并且值得一提的是上述最后的治疗阈值设定，其实真实的染病比隔离所花的钱要多得多，并且考虑到死亡概率就不是所谓的1w每人的惩罚能够对等的了，所以正常但凡出现症状的携带者我们都应该去直接治疗。还有最后的博弈部分其实过于简单了，因为我们设置病毒进化的太强了，必须每天核酸从根源上解决问题= =，这个其实可以自己设置的，可以变难点，问题不大哦。

5.参考文献
[1,2,3,4,5] 年代过于久远且成为教学常识，无法找到原论文
[6] The spread of bacterial infection: the problem of herd immunity, W. W. C. Topley，1923

其实上述的参数乱七八糟的都可以自己调，反正看你想达到一个怎么样的效果就行，不过总体来说都是大同小异的，并且和事实情况也比较贴近，只是说一般疫情没有那么严重罢了。

代码如下：

import numpy as np
import random
import  matplotlib.pyplot as plt
import  time
import mathstate = np.array([])#患者状态 0：易感，1：感染；2：恢复
infected_pro = np.array([])
immunity = np.array([])
current_infected_pro = np.array([])
y1 = [] #都是画图用的
y2=[]
y3 =[]
y4=[]
contact = np.array([])
coordinates = np.array([[0,0]])
action = []
path = [[]]
action_list = ["dormitoryA","library","classroom","playground","canteenA","canteenB","walk_area"]
#字典的每个列表[a,b,c]中，a为密接概率，b为次密接概率，c为无接触概率
area_infection_pro = {"dormitoryA":[0.6,0.3,0.1],"library":[0.1,0.8,0.1],"classroom":[0.2,0.75,0.05],"playground":[0.3,0.5,0.2],"canteenA":[0.5,0.45,0.05],"canteenB":[0.3,0.6,0.1],"walk_area":[0.15,0.2,0.65]}
nop = 10000
#疾病的传染性
r = 10
r0 = np.log(2*r)
curep1 = 0
# r0 = r#初始化最初的感染模型
for i in range(nop):infected_pro = np.append(infected_pro, 0.0)qtmy = random.randint(0, 100)if qtmy < 0:immunity = np.append(immunity,1)else:immunity = np.append(immunity,random.uniform(0.5,0.8))if i != 0:coordinates = np.concatenate((coordinates, np.array([[0,0]])),axis = 0)action.append(action_list[0])contact = np.append(contact,0)#seed = random.randint(0, 2000)#random.seed(1000)flag = random.randint(0, 2000)# print(flag)if flag == 1:state = np.append(state,1)infected_pro[i] = 1.0immunity[i] = 0.0else:state = np.append(state,0)print("初始感染人数：", len([index for index, x in enumerate(infected_pro) if x != 0.0]))
'''
for i in range(10):print(state[i],"-",infected_pro[i],"-",action[i])
'''
days = 30
for day in range(days):times = 0for times in range(5):for i in range(nop):#current_infected_pro = np.append(current_infected_pro, 0.0)if times < 4:  # 每次更新所有人的活动场景action[i] = action_list[random.randint(0, 6)]else:  # 每天最后一次迭代所有人回宿舍action[i] = action_list[0]if times < 4:  # 日常活动时传染情况# 更新每个地区对应人员的健康状况fig = plt.figure(figsize=(12, 6), dpi=100)sub = 1total_infected = 0for act in action_list:ind = [index for index, x in enumerate(action) if x == act]num = len(state[ind])count = 0infected_id = []no_infected_id = []with_infected_id = []mark_infected_id = []# 记录当前已地区所有人的坐标for index in ind:if state[index]!=2:coordinates[index, :] = random.randint(0, num), random.randint(0, num)if infected_pro[index] > 0.1:  # 统计该地区已感染人数infected_id.append(index)if infected_pro[index] >= 0.8:mark_infected_id.append(index)count += 1else:# no_infected_id.append(index)with_infected_id.append(index)else:no_infected_id.append(index)# 更新新的密接与次密接人员for index in ind:if state[index] != 2:if index not in infected_id:# min_dist = numfor id in infected_id:dist = np.sqrt(np.sum(np.square(coordinates[index, :] - coordinates[id, :])))if dist <= r:infected_pro[index] += math.e * (1 - immunity[index]) * np.log(dist + math.e) * \infected_pro[id] / (dist + math.e) * r0elif dist <= 2 * r:infected_pro[index] += math.e * (1 - immunity[index]) * np.log(dist + math.e) / (2 * (dist + math.e)) * infected_pro[id] * r0if infected_pro[index] >= 1:infected_pro[index] = 1axes = plt.subplot(2, 4, sub, facecolor="black")if len(infected_id) != 0:axes.scatter(coordinates[mark_infected_id, 0], coordinates[mark_infected_id, 1], marker='.', color="red")if len(with_infected_id) != 0:axes.scatter(coordinates[with_infected_id, 0], coordinates[with_infected_id, 1], marker='.',color="yellow")if len(no_infected_id) != 0:axes.scatter(coordinates[no_infected_id, 0], coordinates[no_infected_id, 1], marker='.')axes.set_title(act)sub += 1plt.show()else:infected_id = np.array([], dtype=int)recovery = 0for i in range(0,nop,5):# maxindex  = np.argmax(infected_pro[i:i+5])maxindex = 0for k in range(5):if infected_pro[i+k]>infected_pro[maxindex] and state[i+k] != 2:maxindex = kif infected_pro[i+maxindex]>0 and state[i+maxindex]!=2:for m in range(5):if immunity[i+m] != 1:infected_pro[i+m] = infected_pro[i + maxindex]#infected_pro[i:i + 5] = infected_pro[i+maxindex]for j in range(5):touzi = random.randint(0, 10000)if infected_pro[i+j]<0.8 and state[i+j]!=2 and touzi<=9995 and immunity[i+j]!=1:infected_pro[i+j] *= (1-immunity[i+j])if 0<infected_pro[i+j]<0.1:infected_pro[i+j] = 0recovery += 1elif immunity[i+j]!=1:total_infected1 = [index for index, x in enumerate(infected_pro) if x > 0.8 and state[index]!=2]touzi1 = random.randint(0, 10)if (day+1)%7==0 and 0<len(total_infected1)<100:# 第七天变异r+= np.log(500/len(total_infected1))if touzi1>=8:infected_pro[i+j] = 1else:infected_pro[i+j] = 0else:infected_pro[i+j] = 1if touzi>9995 and state[i+j]!=2 and immunity[i+j]!=1:infected_pro[i + j] = 1state[i + j] = 1contact_num = [index for index, x in enumerate(infected_pro) if x != 0.0 and state[index]!=2]total_infected = [index for index, x in enumerate(infected_pro) if x > 0.8]print("***\ndays:",day+1)print("numder of contact_ing:", len(contact_num))print("numder of have_contacted:", len(contact_num)+recovery)print("number of recovery",recovery)print("number of infected:", len(total_infected))y1.append(len(contact_num))y2.append(len(contact_num)+recovery)y3.append(recovery)y4.append(len(total_infected))plt.figure(figsize=(10, 10))x = np.arange(1, day+2)plt.plot(x, y1, '-o', label='numder of contact_ing')plt.plot(x, y2, '-o', label='numder of have_contacted')plt.plot(x, y3, '-o', label='number of recovery')plt.plot(x, y4, '-o', label='number of infected')plt.xlabel("days")plt.ylabel("nop")plt.xticks(np.arange(1, 11))#plt.yticks(np.arange(0, 1, 0.05))# plt.text(x,recall_score,"%.0f" % recall_score)plt.grid()plt.legend()plt.show()#time.sleep(8)times += 1"""if day == 3:curep = 0for i in range(len(infected_pro)):if infected_pro[i] >= 0.2 and state[i] != 2:state[i] = 2  # 拉去隔离curep += 1print("第{}次核酸拉走人数：".format(day // 2 + 1), curep)# curep1 = curep"""if day!=0 and (day+1)%1 == 0:curep = 0for i in range(len(infected_pro)):if infected_pro[i] >=0.2 and state[i]!=2:state[i] = 2 # 拉去隔离curep +=1print("第{}次核酸拉走人数：".format(day//1+1), curep)# curep1 = curepif (day+1)%7==0:# 7天一爆发for i in range(nop):mark = random.uniform(0,1)if mark<infected_pro[i] and state[i]!=2:#if infected_pro[i]>=0.2:infected_pro[i] = 1state[i] = 1else:infected_pro[i] = 0infected_num = [index for index, x in enumerate(state) if x == 1]print(len(infected_num))